Deep Learning Key Terms, Explained
Gain a beginner's perspective on artificial neural networks and deep learning with this set of 14 straight-to-the-point related key concept definitions.
Enjoying a surge in research and industry, due mainly to its incredible successes in a number of different areas, deep learning is the process of applying deep neural network technologies — that is, neural network architectures with multiple hidden layers — to solve problems. Deep learning is a process, like data mining, which employs deep neural network architectures, which are particular types of machine learning algorithms.
Deep learning has racked up an impressive collection of accomplishments in the past several years. In light of this, it's important to keep a few things in mind, at least in my opinion:
- Deep learning is not a panacea - it is not an easy one-size-fits-all solution to every problem out there
- It is not the fabled master algorithm - deep learning will not displace all other machine learning algorithms and data science techniques, or, at the very least, it has not yet proven so
- Tempered expectations are necessary - while great strides have recently been made in all types of classification problems, notably computer vision and natural language processing, as well as reinforcement learning and other areas, contemporary deep learning does not scale to working on very complex problems such as "solve world peace"
- Deep learning and artificial intelligence are not synonymous
- Deep learning can provide an awful lot to data science in the form of additional processes and tools to help solve problems, and when observed in that light, deep learning is a very valuable addition to the data science landscape
So, with that, let's look at some deep learning-related terminology, focusing on concise, no-nonsense definitions.
1. Deep Learning
As defined above, deep learning is the process of applying deep neural network technologies to solve problems. Deep neural networks are neural networks with one hidden layer minimum (see below). Like data mining, deep learning refers to a process, which employs deep neural network architectures, which are particular types of machine learning algorithms.
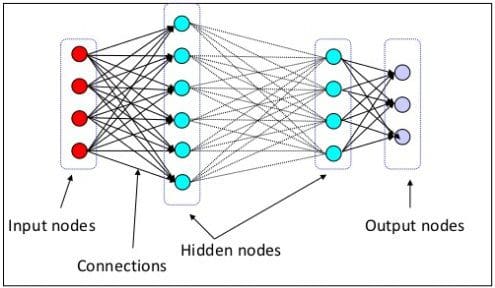
2. Artificial Neural Networks
The machine learning architecture was originally inspired by the biological brain (particularly the neuron) by which deep learning is carried out. Actually, artificial neural networks (ANNs) alone (the non-deep variety) have been around for a very long time, and have been able to solve certain types of problems historically. However, comparatively recently, neural network architectures were devised which included layers of hidden neurons (beyond simply the input and output layers), and this added level of complexity is what enables deep learning, and provides a more powerful set of problem-solving tools.
ANNs actually vary in their architectures quite considerably, and therefore there is no definitive neural network definition. The 2 generally-cited characteristics of all ANNs are the possession of adaptive weight sets, and the capability of approximating non-linear functions of the inputs to neurons.
3. Biological Neuron
Much is often made of the definitive connection between biological and artificial neural networks. Popular publications propagate the idea that ANNs are somehow an exact replica of what's going on in the human (or other biological) brain. This is clearly inaccurate; at best, early artificial neural networks were inspired by biology. The abstract relationship between the 2 are no more definitive than the abstract comparison drawn between the make up and functionality of atoms and the solar system.
That said, it does do us some good to see how biological neurons work at a very high level, if simply to understand the inspiration for ANNs.
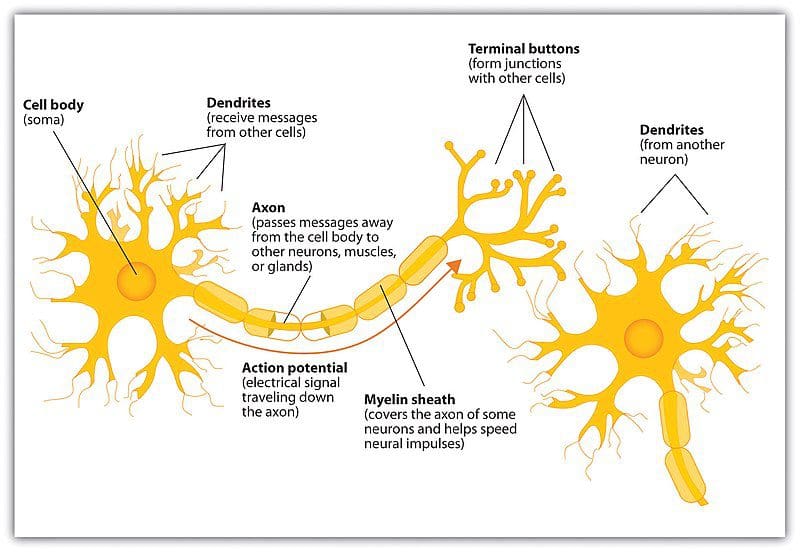
Image source: Wikipedia
The major components of the biological neuron of interest to us are:
- The nucleus holds genetic information (i.e. DNA)
- The cell body processes input activations and converts them to output activations
- Dendrites receive activations from other neurons
- Axons transmit activations to other neurons
- The axon endings, along with neighboring dendrites, form the synapses between neurons
Chemicals called neurotransmitters then diffuse across the synaptic cleft between an axon ending and a neighboring dendrite, constituting a neurotransmission. The essential operation of the neuron is that an activation flows into a neuron via a dendrite, is processed, and is then retransmitted out an axon, through its axon endings, where it crosses the synaptic cleft, and reaches a number of receiving neurons’ dendrites, where the process is repeated.
4. Perceptron
A perceptron is a simple linear binary classifier. Perceptrons take inputs and associated weights (representing relative input importance), and combine them to produce an output, which is then used for classification. Perceptrons have been around a long time, with early implementations dating back to the 1950s, the first of which were involved in early ANN implementations.
5. Multilayer Perceptron
A multilayer perceptron (MLP) is the implementation of several fully adjacently-connected layers of perceptrons, forming a simple feedforward neural network (see below). This multilayer perceptron has the additional benefit of nonlinear activation functions, which single perceptrons do not possess.
6. Feedforward Neural Network
Feedforward neural networks are the simplest form of neural network architecture, in which connections are non-cyclical. The original artificial neural network, information in a feedforward network advances in a single direction from the input nodes, though any hidden layers, to the output nodes; no cycles are present. Feedforward networks differ from later, recurrent network architectures (see below), in which connections form a directed cycle.
7. Recurrent Neural Network
In contrast to the above feedforward neural networks, the connections of recurrent neural networks form a directed cycle. This bidirectional flow allows for internal temporal state representation, which, in turn, allows sequence processing, and, of note, provides the necessary capabilities for recognizing speech and handwriting.
8. Activation Function
In neural networks, the activation function produces the output decision boundaries by combining the network's weighted inputs. Activation functions range from identity (linear) to sigmoid (logistic, or soft step) to hyperbolic (tangent) and beyond. In order to employ backpropagation (see below), the network must utilize activation functions which are differentiable.
9. Backpropagation
The best concise, elementary definition of backpropagation I have ever come across was by data scientist Mikio L. Braun, giving the following answer on Quora, which I reproduce verbatim so as not soil its simple perfection:
Back prop is just gradient descent on individual errors. You compare the predictions of the neural network with the desired output and then compute the gradient of the errors with respect to the weights of the neural network. This gives you a direction in the parameter weight space in which the error would become smaller.
10. Cost Function
When training a neural network, the correctness of the network's output must be assessed. As we know the expected correct output of training data, the output of training can be compared. The cost function measures the difference between actual and training outputs. A cost of zero between the actual and expected outputs would signify that the network has been training as would be possible; this would clearly be ideal.
So, by what mechanism is the cost function adjusted, with a goal of minimizing it?
11. Gradient Descent
Gradient descent is an optimization algorithm used for finding local minima of functions. While it does not guarantee a global minimum, gradient descent is especially useful for functions which are difficult to solve analytically for precise solutions, such as setting derivatives to zero and solving.
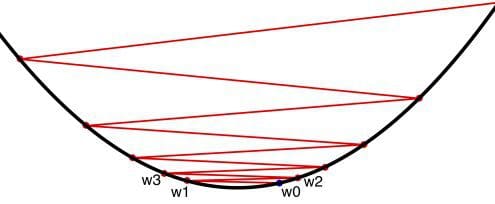
As alluded to above, in the context of neural networks, stochastic gradient descent is used to make informed adjustments to your network's parameters with the goal of minimizing the cost function, thus bringing your network's actual outputs closer and closer, iteratively, to the expected outputs during the course of training. This iterative minimization employs calculus, namely differentiation. After a training step, the network weights receive updates according the gradient of the cost function and the network's current weights, so that the next training step's results may be a little closer to correct (as measured by a smaller cost function). Backpropagation (backward propagation of errors) is the method used to dole these updates out to the network.
12. Vanishing Gradient Problem
Backpropagation uses the chain rule to compute gradients (by differentiation), in that layers toward the "front" (input) of an n-layer neural network would have their small number updated gradient value multiplied n times before having this settled value used as an update. This means that the gradient would decrease exponentially, a problem with larger values of n, and front layers would take increasingly more time to train effectively.
13. Convolutional Neural Network
Typically associated with computer vision and image recogntion, Convolutional Neural Networks (CNNs) employ the mathematical concept of convolution to mimic the neural connectivity mesh of the biological visual cortex.
First, convolution, as nicely described by Denny Britz, can be thought of as a sliding window over top a matrix representation of an image (see below). This allows for the loose mimicking of the overlapping tiling of the biological visual field.

Image credit: Analytics Vidhya
Implementation of this concept in the architecture of the neural network results in collections of neurons dedicated to processing image sections, at least when employed in computer vision. When utilized in some other domain, such as natural language processing, the same approach can be used, given that input (words, sentences, etc.) could be arranged in matrices and processed in similar fashion.
14. Long Short Term Memory Network
A Long Short Term Memory Network (LSTM) is a recurrent neural network which is optimized for learning from and acting upon time-related data which may have undefined or unknown lengths of time between events of relevance. Their particular architecture allows for persistence, giving the ANN a "memory." Recent breakthroughs in handwriting recognition and automatic speech recognition have benefited from LSTM networks.
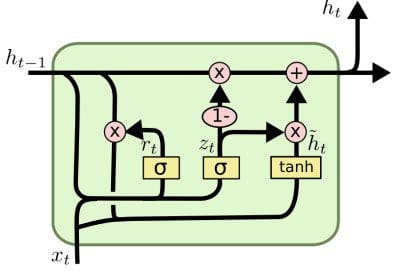
Image credit: Christopher Olah
This is clearly only a small subset of deep learning terminology, and many additional concepts, from elementary to advanced, await your exploration as you learn more about the current leading field in machine learning research.
Matthew Mayo (@mattmayo13) is a Data Scientist and the Editor-in-Chief of KDnuggets, the seminal online Data Science and Machine Learning resource. His interests lie in natural language processing, algorithm design and optimization, unsupervised learning, neural networks, and automated approaches to machine learning. Matthew holds a Master's degree in computer science and a graduate diploma in data mining. He can be reached at editor1 at kdnuggets[dot]com.
