Data Mining Tip: How to Use High-cardinality Attributes in a Predictive Model
High-cardinality nominal attributes can pose an issue for inclusion in predictive models. There exist a few ways to accomplish this, however, which are put forward here.
By Julie Moeyersoms and David Martens, University of Antwerp.
If you work in predictive modeling, you will surely have encountered nominal variables with many distinct values. Think for example of the ZIP code or street name of a person, the university or high-school they studied at, the sector of a business, or even family names or bank account numbers of persons. In the United States for example, there are approximately 43.000 zip codes. Such features could be very predictive as it could be telling that someone lives in a certain village or works in a certain business sector. We call such nominal variables with more than 100 distinct values “high-cardinality attributes”.
Despite their potential, unfortunately such variables are typically discarded in predictive modeling. The main reasons are: firstly, including these attributes by standard dummy encoding increases the dimensionality of the data to such an extent that either the classification technique is unable to process them (with for example decision trees), or if one would use some regularized linear technique that is able to cope with huge dimensions, it leads to a model with thousands or even millions of features, thereby losing the often required comprehensibility aspect. Secondly, for some variable one can try to group the values in some semantic manner, like grouping on a state level for ZIP codes or to the first two digits when using NACE business activity codes, but that is only possible if the data is not anonymized, and additionally one loses important information.
There exist a few ways to include such attributes, which we put forward here. More related research and technical details can be found in our recent paper in Decision Support Systems [3]. An elegant way to include such high cardinality attributes is by transforming the nominal variable to a single continuous one, whose values are correlated with the target label. Three different transformation functions are proposed. Important note: in order to avoid overfitting, the scores for the continuous transformations need to be calculated on a separate part of data. To explain the transformations, we’ll use the example of ZIP codes.
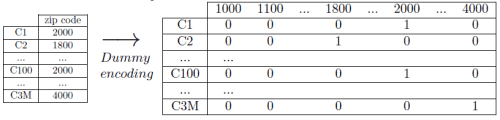
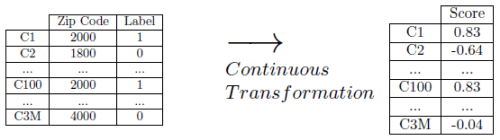
Supervised ratio: the easiest transformation is transforming each ZIP code to the percentage of positive instances in that ZIP code. When predicting churn for example, a person whose ZIP code is 10009 will be given a transformed value of the percentage of churners in that ZIP code. So if the training set consists of 100 customers in ZIP code 10009, 5 of which churned (so Pi=5 and Ni=95) then the transformed value is 0.05. The intuitive nature of the variable makes it very suitable for subsequent use in decision trees and rules.
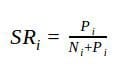
Weight of evidence: this transformation has been used in credit scoring for low-value nominal variables in the past [1]. A nice characteristic of this transformation is that ZIP codes with a less than average churn rate will have a negative value, and a higher than average churn rate will lead to a positive transformed value. For subsequent use of such a variable in linear models, this is surely an advantage. The formula is as follows, with TP and TN denoting the total positive and negative instances respectively.
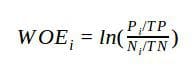
Perlich ratio: the final metric is based on the work of Claudia Perlich and Foster Provost [4], where they propose aggregation operators when working with data that incorporates many-to-many relationships (like persons watching movies or calling numbers). For our one-to-many relationship settings (one ZIP code has many persons, but one person only has one ZIP code), one of their operators transforms neatly to an easy to calculate transformation. For the formula we refer to the paper.
For each of these transformations, we need to consider the special cases where the value is either missing or when the number of positive or negative values for that ZIP code is zero (Pi = 0 or Ni = 0). At that point the transformed value should correspond to the attribute’s average.
We applied these transformation techniques on a real-life data set which stems from a large energy supplier in Belgium. The data set contains more than 1 million data points (customers) and consists of both “traditional” and high-cardinality attributes. The latter are in this case: bank account number, family names and ZIP code which implies that they each include more than 100 distinct values. We observe significant improvement when the variables are included, for both C4.5, logistic regression and a linear SVM classifier, with the best results obtained by the WOE transformation.
An interesting observation also is that having larger datasets leads to better performance! This has already been observed in other big data settings (see eg [2]), but is now also visible in a more “traditional” setting of socio-demographic data. See for example in the figure below, that demonstrates that adding more and more data consistently improves the AUC of the logistic regression model that includes the WOE encoded ZIP codes.
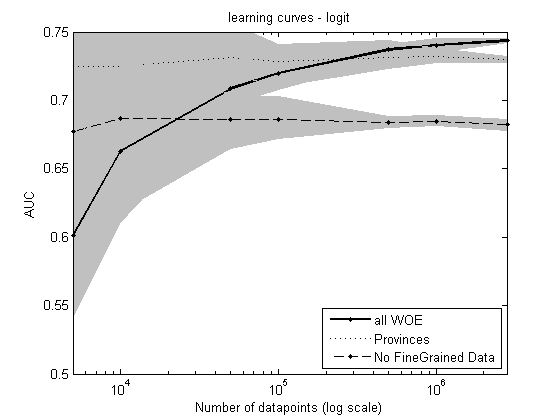
In any domain where predictive modeling is currently being done on a person's level, where for each data point/person we know at least the person's last name or zip code, can the same metrics be applied. Such applications include customer acquisition, response modeling, default prediction, fraud detection, etc. On top of that, even when the data is not related to a person, high-cardinality attributes are often available. Just to demonstrate its widespread use, two examples: the 2014 KDD Cup challenge aimed at predicting whether a project proposal will be funded or not, where high-cardinality attributes are available in the form of school ID and district ID. Imagine the explosion in dimensions if one would add a dummy for each of the 30,000 school IDs or 7,000 district IDs. The proposed metrics on the other hand are fast to calculate and can easily be included in any subsequent classification algorithm. In a corporate fraud detection setting, the last name of the CEO or the specific NACE (activity) code are other potentially useful high-cardinality attributes.
To conclude, research in predictive modeling has a tendency to lead to a continuous flow of new and complex algorithms, which are often applicable only in a very specific setting (if an implementation is made available in the first place). The rather intuitive transformation techniques that we set forth to include attributes that are already available, try to answer the call for better data rather than better modeling techniques. As such, they have a wide applicability and can lead to substantial performance improvements.
References
[1] Hand, D. J., Henley, W. E., 1997. Statistical classification methods in consumer credit scoring: a review. Journal of the Royal Statistical Society: Series A (Statistics in Society) 160 (3), 523-541.
[2] Junqué de Fortuny E., Martens D., Provost F., 2013. Predictive modeling with big data : is bigger really better? Big data 1(4), 215-226.
[3] Moeyersoms J., Martens D., 2015. Including high-cardinality attributes in predictive models a case study in churn prediction in the energy sector. Decision support systems -72 (2015), 72-81.
[4] Perlich, C., Provost, F., 2006. Distribution-based aggregation for relational learning with identifier attributes. Machine Learning 62 (1-2), 65-105.
Julie Moeyersoms graduated in 2012 as a business engineer at the Faculty of Applied Economics at the University of Antwerp. She obtained her Ph.D. at the same University under the supervision of prof. David Martens from the Applied Data Mining Group. The topic of her dissertation is the predictive and economic value of customer behavior data in predictive modeling.
David Martens is professor at the University of Antwerp, where he heads the Applied Data Mining research group. His research focuses on the development and application of data mining techniques using behavior data, and the use thereof in marketing and finance. David is also co-founder of Predicube, a European ad tech company that work on predictive modeling for targeted online advertising.
Related:
