WTF is a Tensor?!?
A tensor is a container which can house data in N dimensions, along with its linear operations, though there is nuance in what tensors technically are and what we refer to as tensors in practice.
What is a Tensor?
When we represent data for machine learning, this generally needs to be done numerically. Especially when referring specifically of neural network data representation, this is accomplished via a data repository known as the tensor.
So what is the meaning of a tensor? A tensor is a container which can house data in N dimensions. Often and erroneously used interchangeably with the matrix (which is specifically a 2-dimensional tensor), tensors are generalizations of matrices to N-dimensional space.
Mathematically speaking, tensors are more than simply a data container, however. Aside from holding numeric data, tensors also include descriptions of the valid linear transformations between tensors. Examples of such transformations, or relations, include the cross product and the dot product. From a computer science perspective, it can be helpful to think of tensors as being objects in an object-oriented sense, as opposed to simply being a data structure.
Tensors in Machine Learning
While the above is all true, there is nuance in what tensors technically are and what we refer to as tensors as relates to machine learning practice. If we temporarily consider them simply to be data structures, below is an overview of where tensors fit in with scalars, vectors, and matrices, and some simple code demonstrating how Numpy can be used to create each of these data types. We will look at some tensor transformations in a subsequent post.
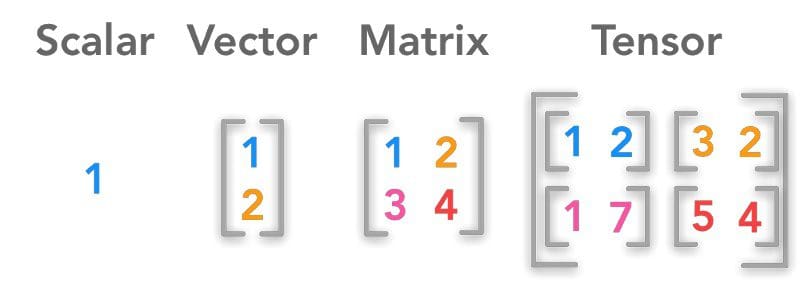
Image source
Scalar
A single number is what constitutes a scalar. A scalar is a 0-dimensional (0D) tensor. It, thus, has 0 axes, and is of rank 0 (tensor-speak for 'number of axes').
And this is where the nuance comes in: though a single number can be expressed as a tensor, this doesn't mean it should be, or that in generally is. There is good reason to be able to treat them as such (which will become evident when we discuss tensor operations), but as a storage mechanism, this ability can be confounding.
Numpy's multidimensional array ndarray is used below to create the example constructs discussed. Recall that the ndim attribute of the multidimensional array returns the number of array dimensions.
import numpy as np
x = np.array(42)
print(x)
print('A scalar is of rank %d' %(x.ndim))
42 A scalar is of rank 0
Vector
A vector is a single dimension (1D) tensor, which you will more commonly hear referred to in computer science as an array. An vector is made up of a series of numbers, has 1 axis, and is of rank 1.
x = np.array([1, 1, 2, 3, 5, 8])
print(x)
print('A vector is of rank %d' %(x.ndim))
[1 1 2 3 5 8] A vector is of rank 1
Matrix
A matrix is a tensor of rank 2, meaning that it has 2 axes. You are familiar with these from all sorts of places, notably what you wrangle your datasets into and feed to your Scikit-learn machine learning models :) A matrix is arranged as a grid of numbers (think rows and columns), and is technically a 2 dimension (2D) tensor.
x = np.array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])
print(x)
print('A matrix is of rank %d' %(x.ndim))
[[1 4 7] [2 5 8] [3 6 9]] A matrix is of rank 2
3D Tensor & Higher Dimensionality
While, technically, all of the above constructs are valid tensors, colloquially when we speak of tensors we are generally speaking of the generalization of the concept of a matrix to N ≥ 3 dimensions. We would, then, normally refer only to tensors of 3 dimensions or more as tensors, in order to avoid confusion (referring to the scalar '42' as a tensor would not be beneficial or lend to clarity, generally speaking).
The code below creates a 3D tensor. If we were to pack a series of these into a higher order tensor container, it would be referred to as a 4D tensor; pack those into another order higher, 5D, and so on.
x = np.array([[[1, 4, 7],
[2, 5, 8],
[3, 6, 9]],
[[10, 40, 70],
[20, 50, 80],
[30, 60, 90]],
[[100, 400, 700],
[200, 500, 800],
[300, 600, 900]]])
print(x)
print('This tensor is of rank %d' %(x.ndim))
[[[ 1 4 7] [ 2 5 8] [ 3 6 9]] [[ 10 40 70] [ 20 50 80] [ 30 60 90]] [[100 400 700] [200 500 800] [300 600 900]]] This tensor is of rank 3
What you do with a tensor is your business, though understanding what one is, and its relationship to related numerical container constructs, should now be clear.
Matthew Mayo (@mattmayo13) is a Data Scientist and the Editor-in-Chief of KDnuggets, the seminal online Data Science and Machine Learning resource. His interests lie in natural language processing, algorithm design and optimization, unsupervised learning, neural networks, and automated approaches to machine learning. Matthew holds a Master's degree in computer science and a graduate diploma in data mining. He can be reached at editor1 at kdnuggets[dot]com.
