
3 Ways Understanding Bayes Theorem Will Improve Your Data Science
Mastery of this intuitive statistical concept will advance your credibility as a decision-maker.

Photo by Ella Olsson from Pexels
Bayes Theorem gives us a way of updating our beliefs in light of new evidence, taking into account the strength of our prior beliefs. Deploying Bayes Theorem, you seek to answer the question: what is the likelihood of my hypothesis in light of new evidence?
In this article, we’ll talk about three ways that the Bayes Theorem can improve your practice of Data Science:
- Updating
- Communicating
- Classifying
By the end, you’ll possess a deep understanding of the foundational concept.
#1 — Updating
Bayes Theorem provides a structure for testing a hypothesis, taking into account the strength of prior assumptions and the new evidence. This process is referred to as Bayesian Updating.
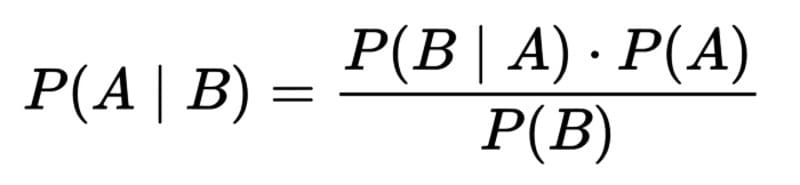
Bayes Theorem, where A represents the hypothesis, and B represents new evidence relevant to the hypothesis.
In words, this formula is “likelihood of A given B equals (open parentheses) likelihood of B given A times the likelihood of A (close parentheses) divided by the likelihood of B.”
Let’s go through the formula again, this time with definitions of the variables:
“The likelihood of the hypothesis in light of new evidence equals the likelihood of the new evidence being true assuming the hypothesis is also true times the likelihood of the hypothesis before the new evidence was observed, all over (divided by) the likelihood of the new evidence.”
This can be further shortened:
“The posterior probability equals the likelihood times the prior probability divided by the marginal likelihood.”
Whether or not Bayes Theorem sounds intuitive right now, I guarantee you use it all the time.
Real world example
Let’s say your friend calls to tell you that she’s very sorry, but she cannot make it to dinner tonight. She’s recently adopted a pet koala who has developed a case of the sniffles. She really needs to stay home to monitor the situation.
Your hypothesis is that your friend wouldn’t ditch you for no good reason. (After all, you make a mean ph? that your friend would be crazy to skip out on.) What is the likelihood that your hypothesis is true given the recent evidence of her new pet?

Photo by Valeriia Miller from Pexels
In order to evaluate the posterior probability that our friend isn’t at dinner because she’s taking care of a koala, we need to consider the likelihood of your friend needing to stay home with the koala given the hypothesis that your friend is an upstanding person who doesn’t ditch dinner plans without good reason. You might conclude there’s a high likelihood that a good friend who is typically responsible would stay home to look after a pet.
Next, we multiply the likelihood by the prior probability. Before your friend called, how strong was your belief in her commitment to dinner plans? If you believe your friend is rock solid and typically unwilling to change plans at the last minute, then your prior probability is strong, and you would be unlikely to change this view, irrespective of new evidence. On the other hand, if your friend is flakey and you were already wondering whether she’d call to cancel, your prior probability is weak, which may also call into question her claim about staying home with the koala.
Finally, we divide the above calculation by the marginal likelihood of koala ownership ??
Bayesian inference is built on this flexible, common-sense way of updating our models about the world based on the strength of our priors and the likelihood of new evidence. In fact, the initial application of Bayes Theorem was to evaluate the existence of god.
When it comes to crucial questions of life and Data Science, you can’t beat Bayes Theorem as an intuitive way of assessing how beliefs change over time.
#2 — Communicating
Just as Bayes Theorem can help you understand and articulate how you update your theories in the face of new evidence, Bayes can also make you a stronger Data Science communicator.
Data Science is fundamentally about the application of data to improve decision making.
There are only two things that determine how your life turns out: luck and the quality of your decisions. You have control over only one of those two things. — Annie Duke, poker champion and author
Improving decision quality often means convincing the decision-maker. As is the case for every human, the decision-maker at your organization is entering the conversation
Real world example
I was once a consultant for a hot air balloon manufacturer. My task was to help set up a database that would improve the client’s end-to-end understanding of their supply chain, manufacturing processes, and sales.
As the plant manager toured us around the floor on day one, he proudly described a new supplier contract for lighter, cheaper input material.
But there was a problem. As my team connected data tables from disparate data sources across the enterprise, we discovered a connection between the materials from the new vendor and a 2.5% increase in scrap.

Photo by Darren Lee on Unsplash
The plant manager had a very strong prior that the new supplier was a net positive for his business. We had some evidence to the contrary. We also had Bayes Theorem. And we understood this fact:
The stronger the prior, the more evidence needed to change it.
Before approaching the plant manager with our findings, we needed to collect additional evidence that there wasn’t some other factor, (e.g. worn-out machines, new employees, environmental conditions, etc.) contributing to the differing scrap level.
Eventually, we approached the manager with more evidence and helped him renegotiate the supplier contract.
#3 — Classifying
Bayes Theorem can be applied to text analytics use cases, a technique called naive Bayes because it naively assumes the independence of each input variable (in this case, each word) in the dataset.
Real world example
Let’s say you found a bunch of letters written by your grandparents. They had a bit of a tumultuous relationship with enough drama to prove that rocky romances aren’t confined to young people on reality tv.

Photo by RODNAE Productions from Pexels
You want to build a sentiment classifier to determine whether the majority of the content is positive or negative. One way to do this is to utilize naive Bayes.
A generative classifier like naive Bayes will build a model of how a class (in this case, positive or negative) could generate some input data. Given an observation (a new sentence from our letters test corpus), it returns the class most likely to have generated the observation. This is in contrast to a discriminative classifier such as logistic regression that learns the predictive power of input features.
Naive Bayes is built upon the technique of bag-of-words — basically transforming the document into a histogram that tallies how many times each word is used.
You can use a slightly modified version of the Bayesian inference formula that we studied in Part #1 to compute the most probable class for each observation. The slight modification is the naive part of naive Bayes: the assumption that the probabilities for each word are independent given the class, so you can therefore multiply them together to generate the probability of the sentence falling with the class.
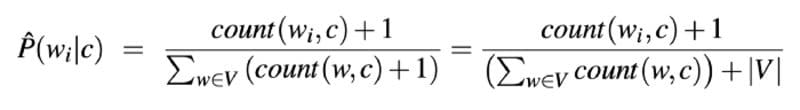
via Speech and Language Processing by Daniel Jurafsky & James H. Martin
In the formula above, w? represents the count of a word in the document c. The denominator of the formula is the sum of the conditional probabilities that the words fall into the given class.
The +1 in the formula prevents any chance of multiplying by zero in the case where there are no observations of a word within a class. This technique of adding one is called Laplace smoothing.
Finally, |V| consists of the union of all the words in all classes.
Bayes Theorem vocabulary
- Posterior probability: the likelihood of the hypothesis in light of new evidence
- Likelihood: the likelihood of the evidence being true, assuming the hypothesis is true
- Prior probability: the strength of your belief that the hypothesis is true, prior to the new evidence coming to light
- Marginal likelihood: the evidence
- Naive Bayes: a classifier algorithm that assumes naive independence between features of the dataset
- generative classifier: models how a particular class would generate input data
- bag-of-words: a simplifying representation of a text that transforms the document into a histogram
- Laplace smoothing: a simple additive smoothing technique to avoid multiplying by zero
Summary
I have a strong prior belief that Bayes Theorem is useful to data scientists, but I’ll be updating the posterior probability based on the feedback you leave me in the comments. I look forward to hearing from you about how you use Bayes Theorem in your life and work.
Original. Reposted with permission.
