Genetic Algorithm Key Terms, Explained
This article presents simple definitions for 12 genetic algorithm key terms, in order to help better introduce the concepts to newcomers.
Genetic algorithms, inspired by natural selection, are a commonly used approach to approximating solutions to optimization and search problems. Their necessity lies in the fact that there exist problems which are too computationally complex to solve in any acceptable (or determinant) amount of time.
Take the well-known travelling salesman problem, for example. As the number of cities involved in the problem grow, the time required for determining a solution quickly becomes unmanageable. Solving the problem for 5 cities, for example, is a trivial task; solving it for 50, on the other hand, would take an amount of time so unreasonable as to never complete.
It turns out that approximating such optimization problems with genetic algorithms is a sensible approach, resulting in reasonable approximations. Genetic algorithms have had a place in the machine learning repertoire for decades, but their recent revival as tools for optimizing machine learning hyperparameters (and traversing neural network architecture search spaces) has brought them to the attention of a new generation of machine learning researchers and practitioners.
This article presents simple definitions for 12 genetic algorithm key terms, in order to help better introduce the concepts to newcomers.
1. Genetic Algorithm
A genetic algorithm (GA) characterizes potential problem hypotheses using a binary string representation, and iterates a search space of potential hypotheses in an attempt to identify the "best hypothesis," which is that which optimizes a predefined numerical measure, or fitness. GAs are, collectively, a subset of evolutionary algorithms.
2. Evolutionary Algorithm
An evolutionary algorithm (EA) is any type of learning method motivated by their obvious and intentional parallels to biological evolution, including, but not limited to, genetic algorithms, evolutionary strategies, and genetic programming.
3. Genetic Programming
Genetic programming is a specific type of EA which leverages evolutionary learning strategies to optimize the crafting of computer code, resulting in programs which perform optimally in a predefined task or set of tasks.
4. Population
In a GA, each iteration, or generation, results in a series of possible hypotheses for best approximating a function, and the population refers to the complete set or pool of these generated hypotheses after a given iteration.
5. Chromosome
In an obvious nod to biology, a chromosome is a single hypothesis of which many make up a population.
6. Gene
In a GA, potential hypotheses are made up of chromosomes, which are, in turn, made up of genes. Practically, in a GA, chromosomes are generally represented as binary strings, a series of 1s and 0s, which denote inclusion or exclusion of particular items represented by position in the string. A gene is a single bit within such a chromosome.
For example, the Hello World of genetic algorithms is often considered to be the knapsack problem. In this problem, there would be a set of N items which may or may not be included in a thief's knapsack, and these N items would be represented as a binary string (the chromosome) N characters long, with each position in the string representing a particular item and the positional bit (1 or 0; the gene) denoting whether the item is included in the particular hypothesis or not.
- Population → all of the proposed solutions to the knapsack problem of the current generation (iteration of the algorithm)
- Chromosome → a particular proposed solution to the knapsack problem
- Gene → positional representation of a particular item (and its inclusion or exclusion) in the knapsack of a particular solution to the knapsack problem
7. Generation
In GAs, new sets of hypotheses are formed from previous sets of hypotheses, either by selecting some full chromosome (generally of high fitness) to move forward to a new generation unscathed (selection), by flipping a bit of an existing full chromosome and moving it forward to a new generation (mutation), or, most commonly, by breeding child chromosomes for the new generation by using an existing set's genes as parents.
A generation, then, is simply the full set of the results of a GA iteration.
8. Breeding
Breeding refers to what is generally the most common method of creating new chromosomes from an existing generation's set of hypotheses, which is using a pair of said chromosomes as parents and creating from them new child chromosomes, using the crossover method.
9. Selection
In a nod to natural selection, the concept of selection is ensuring that the best performing (highest fitness) chromosomes are ensured a higher probability of being used for breeding the next generation. Often highest performing chromosomes may be selected and pushed forward into the new generation without being used for breeding, ensuring that subsequent generations of hypotheses will minimally perform at the same level of the current generation.
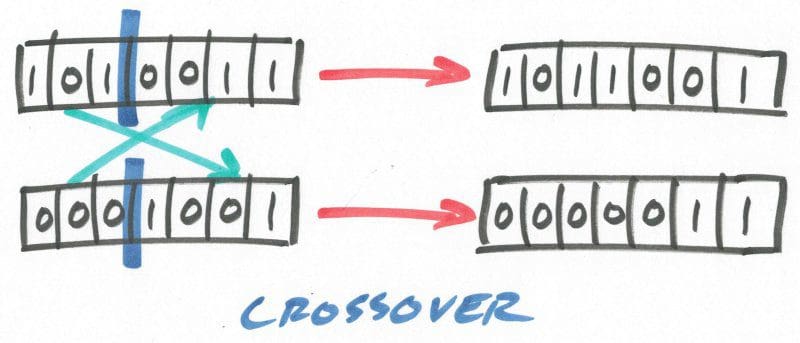
10. Crossover
How are selected chromosomes used to breed subsequent generations? The crossover method, shown below, is the general choice. A pair of selected strings of N bits in length would be chosen, and a random integer c generated as point of crossover of some size (say, 0 < c < N). The 2 strings are then independently split at this crossover point c and reassembled using the head of one string and the tail of the other, forming a pair of new chromosomes. The fitness of these new hypotheses would then be assessed in the following generation.
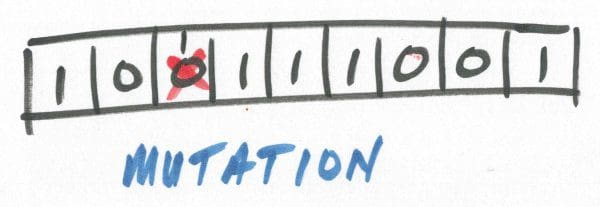
11. Mutation
Just like in biological terms, mutation is used in GAs in order to push hypotheses toward optimal. Generally used sparingly, mutation would simply flip the bit of a random gene and push the entire chromosome forward to the subsequent generation, a strategy for escaping potential local minima.
12. Fitness
We need some metric to measure the best fit of a hypothesis. Some fitness function is used to evaluate each chromosome, and best fits can be identified and more heavily relied upon in order to create new generational chromosomes. The fitness function is heavily task-dependent.
Matthew Mayo (@mattmayo13) is a Data Scientist and the Editor-in-Chief of KDnuggets, the seminal online Data Science and Machine Learning resource. His interests lie in natural language processing, algorithm design and optimization, unsupervised learning, neural networks, and automated approaches to machine learning. Matthew holds a Master's degree in computer science and a graduate diploma in data mining. He can be reached at editor1 at kdnuggets[dot]com.
