Why Data Scientists Love Gaussian
Gaussian distribution model, often identified with its iconic bell shaped curve, also referred as Normal distribution, is so popular mainly because of three reasons.
By Abhishek Parbhakar, Data Scientist
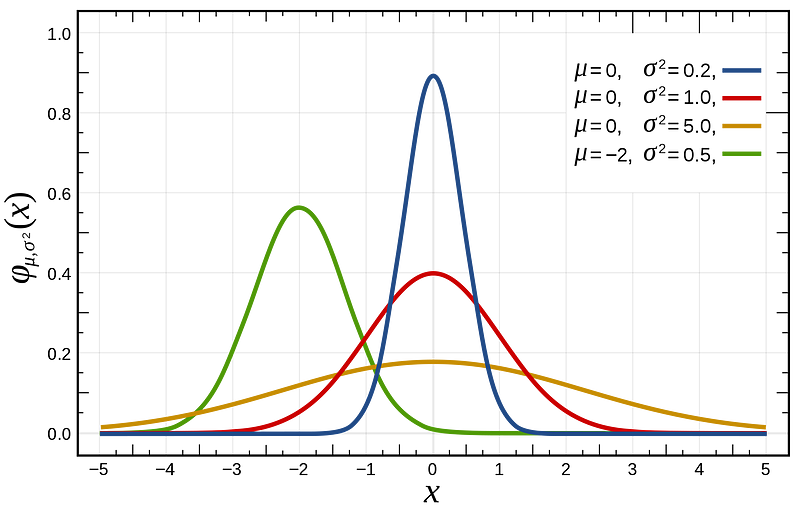
For Deep Learning & Machine Learning engineers out of all the probabilistic models in the world, Gaussian distribution model simply stands out. Even if you have never worked on an AI project, there is a significant chance that you have come across the Gaussian model.
Gaussian distribution model, often identified with its iconic bell shaped curve, also referred as Normal distribution, is so popular mainly because of three reasons.
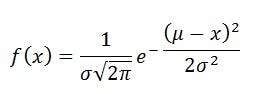
Mathematical formula for Gaussian probability distribution function.
Ubiquitous in natural phenomena
All models are wrong but some are useful! — George Box

Position of particles that experience diffusion can be described using a Gaussian distribution.
Incredible number of processes in nature and social sciences naturally follows the Gaussian distribution. Even when they don’t, the Gaussian gives the best model approximation for these processes. Some examples include-
- Our height, blood pressure of adult human and intelligence
- Position of a particle that experiences diffusion
- Measurement errors
Mathematical Reason: Central Limit Theorem

Random walk in two dimension with two million steps.
Central limit theorem states that when we add large number of independent random variables, irrespective of the original distribution of these variables, their normalized sum tends towards a Gaussian distribution. For example, the distribution of total distance covered in an random walk tends towards a Gaussian probability distribution.
The theorem’s implications include that large number of scientific and statistical methods that have been developed specifically for Gaussian models can also be applied to wide range of problems that may involve any other types of distributions.
The theorem can also been seen as a explanation why many natural phenomena follow Gaussian distribution.
Once a Gaussian, always a Gaussian!
Unlike many other distribution that changes their nature on transformation, a Gaussian tends to remain a Gaussian.
- Product of two Gaussian is a Gaussian
- Sum of two independent Gaussian random variables is a Gaussian
- Convolution of Gaussian with another Gaussian is a Gaussian
- Fourier transform of Gaussian is a Gaussian
Simplicity

Occam Razor is a philosophical principle that emphasized that the simpler solution is the best one given that all other things are same.
For every Gaussian model approximation, there may exist a complex multi-parameter distribution that gives better approximation. But still Gaussian is preferred because it makes the math a lot simpler!
- Its mean, median and mode are all same
- The entire distribution can be specified using just two parameters- mean and variance
Gaussian distribution is named after great mathematician and physicist Carl Friedrich Gauss.
Bio: Abhishek Parbhakar is a Data Scientist finding equilibria among AI, philosophy, and economics.
Original. Reposted with permission.
Related:
- Data Science Basics: Power Laws and Distributions
- Central Limit Theorem for Data Science
- Plausibility vs. probability, prior distributions, and the garden of forking paths
