Game Theory Reveals the Future of Deep Learning

comments

If you’ve been following my articles up to now, you’ll begin to perceive, what’s apparent to many advanced practitioners of Deep Learning (DL), is the emergence of Game Theoretic concepts in the design of newer architectures.

This makes intuitive sense for two reasons. The first intuition is that DL systems will eventually need to tackle situations with imperfect knowledge. In fact we’ve already seen this in DeepMind’s AlphaGo that uses partial knowledge to tactically and strategically best the world-best human in the game of Go.

The second intuition is that systems will not remain monolithic as they are now, but rather would involve multiple coordinating (or competing) cliques of DL systems. We actually already do see this now in the construction of adversarial networks. Adversarial networks consists of competing neural networks, a generator and discriminator, the former tries to generate fake images while the later tries to identify real images. The interesting feature of these systems is that a closed form loss function is not required. In fact, some systems have the surprising capability of discovering its own loss function! A disadvantage of adversarial networks are they are difficult to train. Adversarial learning consists in finding a Nash equilibrium to a two-player non-cooperative game. Yann Lecun, in a recent lecture on unsupervised learning, calls adversarial networks the “the coolest idea in machine learning in the last twenty years”.

We are still in the early stages here of leveraging game thoery, but I will point out some papers that have a game theoretic bent in them. David Balduzzi has a framework for deep learning that takes a game theoretic approach. In his paper “Semantics, Representations and Grammars of Deep Learning” he writes:

A potential criticism is that the formulation is too broad. … Nevertheless, it is possible to carve out an interesting subclass of non-convex games by identifying the composition of simple functions as an essential feature common to deep learning architectures. Compositionality is formalized via distributed communication protocols and grammars.

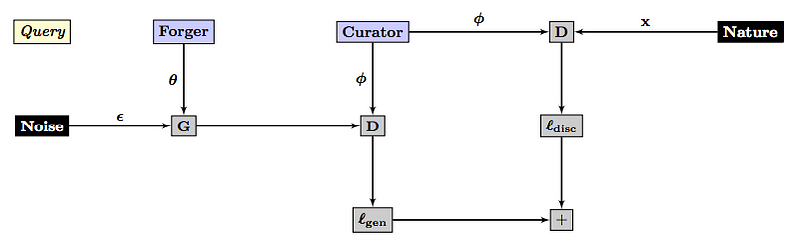
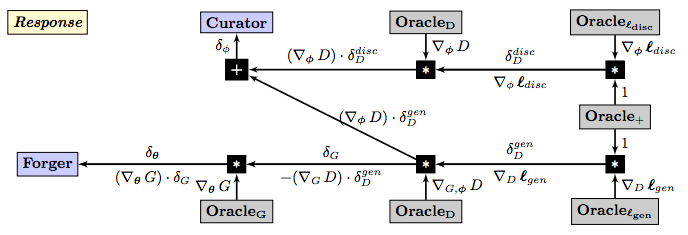
It is a very elegant approach to covering an otherwise bewildering subject. He has these nice graphs (on adversarial networks) that highlight the strength of his approach:

I would really love to see an entire text book written with this approach!

David Silver and Johannes Heinrich have a paper titled “Deep Reinforcement Learning from Self-Play in Imperfect-Information Games”. They write:

We have introduced NFSP, the first end-to-end deep reinforcement learning approach to learning approximate Nash equilibria of imperfect-information games from self-play. Unlike previous game theoretic methods, NFSP is scalable without prior domain knowledge. Furthermore, NFSP is the first deep reinforcement learning method known to converge to approximate Nash equilibria in self-play.

Jason Hartford et al, employs Deep Learning to predict human behavior. They write in “Deep Learning for Predicting Human Strategic Behavior”:

The behavioral game theory literature has developed a wide range of models for predicting human behavior in strategic settings by incorporating cognitive biases and limitations derived from observations of play and insights from cognitive psychology

What we see in these 3 players are 3 different ways game theory plays in Deep Learning. (1) As a means of describing and analyzing new DL architectures. (2) As a way to construct a learning strategy and (3) A way to predict behavior of human participants. The last application can make your skin crawl!

Mathematics provides us with abstractions that aid us in our understanding of complex systems. However, every form of abstraction has its limitations in that there are certain details that are glossed over. We can sketch out some intuition with geometry, dynamics and logic as to how these kind of systems will tend to behave. What we begin to gleam from this is that these systems consist of classifiers built from other classifiers. They are a self similar system that should be treated as a collective of many interacting machines. Furthermore, these machines are designed to make predictions out of the future. These predictions need to performed using incomplete and imperfect data. Therefore we need a mathematical framework that studies the behavior of many interacting parties that are have different sets of information.

The classical view of machine learning is that the problem can be cast as an optimization problem where all that is needed are algorithms that are able to search for an optimal solution. However, with machine learning we want to build machines that don’t overfit the data but rather is able to perform well on data that it has yet to encounter. We want these machines to make predictions about the unknown. This requirement, which is called generalization, is very different from the classical optimization problem. It is very different from the classical dynamics problem where all information is expected to be available. That is why, a lot of the engineering in deep learning requires additional constraints on the optimization problem. These, to my disliking are called ‘priors’ in some texts and also called regularizations in an optimization problem.

Where do these regularizations come from and how can we select a good regularization? How do we handle impartial information? This is where a game theoretic viewpoint becomes important. Generalization is sometimes referred to as ‘structural risk minimization’. In other words, we build mechanisms to handle generalization using strategies similar to how parties mitigate risk. So we have actually returned full circle. Game theory is described as “the study of mathematical models of conflict and cooperation between intelligent rational decision-makers.” In our quest of understanding learning machines we end up with mathematics that were meant for the study of the interactions of intelligent beings.

Feel to jump into the conversation by requesting an invite at LinkedIn:
www.linkedin.com/groups/8584076.

Bio: Carlos Perez is a software developer presently writing a book on "Design Patterns for Deep Learning". This is where he sources his ideas for his blog posts.

Original. Reposted with permission.

Related:

• The Five Capability Levels of Deep Learning Intelligence
• Why Deep Learning is Radically Different From Machine Learning
• Deep Learning Key Terms, Explained