New Hybrid Rare-Event Sampling Technique for Fraud Detection

comments

By Ross Bettinger.

I once had a fraud detection problem involving 2,000 observations labeled Fraudulent out of 1,000,000 total population, a 0.2% event rate. My immediate thought was to stratify the sample into equal numbers of fraudulent and non-fraudulent observations, build models on the biased sample, and use prior probabilities to correct for sampling bias. But given the requirement of creating training/validation/test datasets (say 70%/20%/10% proportions), will only 1,400 training events represent sufficient and consistent behavior containing enough features to represent fraudulent behavior when the target population is so small?

If I use bagging, I have to select fractions of the total population (or even of a sampled population) and build unbiased or biased models. If I build cross-validation models, I have the same problem. When assembling the training data, I typically select subsets of the fraudulent observations and combine them with subsets of the non-fraudulent observations. Regardless of the proportions, I do not use ALL of the fraudulent observations in a given model because of the model building methodology. Thus, I weaken the model’s power of detection at the outset.

Figure 1 illustrates this strategy. Each sample uses a fraction of the potential maximum number of observations proportional to the training/validation/test ratios. The training, validation, and holdout datasets containing 2,000 rare events are labeled S_T,S_V,and S_H and the nonevents are not shown because their numbers may vary, depending on the sampling proportions of event/nonevent.

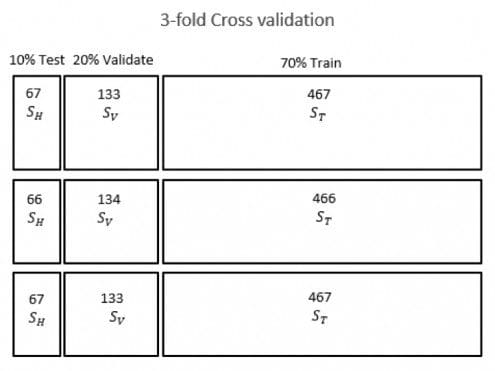
Aside from the holdout sample which is not used in model construction, if I use fewer than all of the remaining fraudulent cases (e.g., 70% for the training dataset, 20% for the validation dataset) in a model, I may be losing important information since I am trying to identify fraud patterns, and each scarce event is valuable because it represents an example of the behavior that I am trying to detect.

My primary problem is: how do I use as many of the fraudulent examples in the training process as possible without resorting to oversampling, SMOTE-based over- and underrepresentation, or inverse probability weighting?

So, I devised the following sampling construction methodology:

• Let us label the set of fraudulent observations as Signal (S) and non-fraudulent observations as Noise (N).
• Then we want to assign labels “S” to observations {S+N} in such a way as to optimize some appropriate performance metric such as AUROC or lift or other KPI.
• Let S_T be the subset of S observations to be used in the training sample, let S_V represent the subset of cases available for validation, and let S_Hrepresent the {S - S_T - S_V}subset of cases available for testing model performance.
• Similarly, let N_T, N_V, and N_H represent subsets of Noise observations.
• We compute subsets of N_T as N_T1,N_T2, ... to contain disjoint samples from N_T.
• We build models from training datasets (S_T, S_V, S_H, N_T1), (S_T, S_V, S_H, N_T2), (S_T, S_V, S_H, N_T3) with corresponding validation and test datasets using noise subsets N_T1, N_V1, and N_H1, et cetera.We use ALL of the S_T,S_V, S_H subsets ofobservations per model and the subsets N_Tn, N_Vn,and N_Hn per model to effectively hold the Signal constant and vary the Noise.
• We use an appropriate ensemble technique to combine the results of the models' predictions and we evaluate KPIs appropriate to our problem’s knowledge domain.

Figure 2 illustrates this strategy. Each dataset uses the maximum number of rare events, and the noise subsets N_Tn, N_Vn,and N_Hn, which are not shown in the figure, are varied for each model.

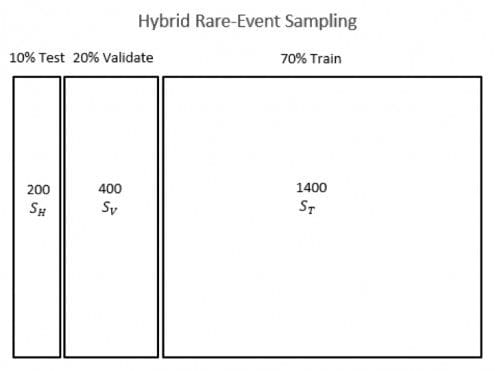
While we may, in theory, assume that all of the data are homogeneously distributed over all of the samples selected, it is good practice to vary the random number seed(s) used in selecting the training, validation, and test datasets and to build several models with the resampled data to ensure that our results are replicable and not merely due to serendipitous happenstance.

This technique is not very different from n-fold cross-validation or bagging except that it uses ALL of the target events in EVERY model instead of disjoint subsets of the target events. The signal S is maintained fixed over all models built and the background noise N is changed.

Essentially, I am proposing to maximize the signal/noise ratio by holding the Signal information constant and varying the Noise information. To ensure the uniformity of the Noise samples being created, the modeler would have to verify that the composition of the Noise samples were consistent with each other. We may assume (in theory) that they are equivalent in information content, but rigorous verification at the outset may preclude time lost in explaining why several models’ results differ widely.

Bio: Ross Bettinger is a data scientist and statistician who enjoys the transformational process of converting data into golden nuggets of information for client use. He applies ML techniques, statistical theory, and experiential intuition to the knowledge discovery process.

• Data Mining Medicare Data – What Can We Find?
• Very Fast Sampling Algorithms for Big Data
• Fraud Detection Solutions