Why Deep Learning Works – Key Insights and Saddle Points
A quality discussion on the theoretical motivations for deep learning, including distributed representation, deep architecture, and the easily escapable saddle point.
By Matthew Mayo.
This post summarizes the key points of a recent blog post by Rinu Boney, based on a lecture by Dr. Yoshua Bengio from this year's Deep Learning Summer School in Montreal, which discusses the theoretical motivations for deep learning.

"To generalize locally, we need representative examples for all relevant variations."
Deep learning is about learning multiple levels of representations, corresponding to multiple levels of abstractions. If we are able to learn these multiple levels of representation, we are able to generalize well.
After setting the general tone of the post with the above (paraphrased) statement, the author presents a number of different artificial intelligence (AI) strategies, from rule-based systems to deep learning, and notes on at which levels of learning their components function. He then states the 3 keys to moving from machine learning (ML) to true artificial intelligence: Lots of data, very flexible models, and powerful priors, and that, since classical ML can handle the first 2, his post deals with the third.
On the path toward AI from today's ML systems, we need learning, generalization, ways to fight the curse of dimensionality, and the ability to disentangle the underlying explanatory factors. Before explaining why non-parametric learning algorithms won't get us to true AI, he gives a nuanced definition of non-parametric. He explains why smoothness, a classical non-parametric approach, won't work on high-dimensionality, and then provides the following insight re: dimensionality:

"A line is very smooth. A curve with some ups and downs is less smooth but still smooth."
So, it's clear that smoothness will not beat the curse of dimensionality alone. In fact, smoothness doesn't even apply to modern, complex problems like computer vision or natural language processing. After discussing the downfalls of such competing methods as Gaussian kernels, Boney sets his sights on moving past smoothness, and why that's necessary:
He notes that in deep learning, 2 priors are used, namely distributed representations and deep architecture.
Why distributed representations?
In distributed representations, features are individually and independently meaningful, and they remain so regardless of what the other features are. There maybe some interactions but most features are learned independent of each other. Boney states that neural networks are very good at learning representations capturing the semantic aspects, and that their generalization power is derived from these representations. As a practical exploration of the topic, he recommend's Cristopher Olah's article for some information on distributed representation and Natural Language Processing.
There is a lot of misunderstanding about what depth means.
Boney then comes full circle. He explains that one of the reasons neural network research was abandon (once again) in the late 90s was because the optimization problem is non-convex. The realization from the work in the 80s and 90s that neural networks have an exponential number of local minima, along with the breakout success of kernel machines, also led to this downfall, as did the fact that networks may get stuck on poor solutions. Recently we have evidence that the issue of non-convexity may be a non-issue, which changes its relationship vis-a-vis neural networks.

"A saddle point is illustrated in the image above. In a global or local minima, all the directions are going up and in a global or local maxima, all the directions are going down."
Saddle Points.
The intuition with the saddle point, is that, for a minima located close to the global minima, all directions should be climbing upward; going further downward is not possible. Local minima exist, but are very close to global minima in terms of objective functions, and theoretical results suggest that some large functions have their probability concentrated between the index (the critical points) and the objective function. The index is the fraction of directions moving downward; for all values of index not 0 or 1 (local minima and maxima, respectively), then it is a saddle point.
Boney goes on to say that there has been empirical validation corroborating this relationship between index and objective function, and that, while there is no proof the results apply to neural network optimization, some evidence suggests that the observed behavior may well correspond to the theoretical results. Stochastic gradient descent, in practice, almost always escapes from surfaces that are not local minima.
This all suggests that local minima may not, in fact, be an issue because of saddle points.
Boney follows his saddle points discussion up by pointing out a few other priors that work with deep distributed representations; human learning, semi-supervised learning, and multi-task learning. He then lists a few related papers on saddle points.
Rinu Boney has written a detailed piece on the motivations for deep learning, including a good discussion on saddle points, all of which is difficult to do justice with a few quotes and some summarization. If you are interested in a deeper discussion of the above points to visit Boney's blog and read the insightful and well-written piece yourself.
Bio: Matthew Mayo is a computer science graduate student currently working on his thesis parallelizing machine learning algorithms. He is also a student of data mining, a data enthusiast, and an aspiring machine learning scientist.
Related:
This post summarizes the key points of a recent blog post by Rinu Boney, based on a lecture by Dr. Yoshua Bengio from this year's Deep Learning Summer School in Montreal, which discusses the theoretical motivations for deep learning.
"To generalize locally, we need representative examples for all relevant variations."
Deep learning is about learning multiple levels of representations, corresponding to multiple levels of abstractions. If we are able to learn these multiple levels of representation, we are able to generalize well.
After setting the general tone of the post with the above (paraphrased) statement, the author presents a number of different artificial intelligence (AI) strategies, from rule-based systems to deep learning, and notes on at which levels of learning their components function. He then states the 3 keys to moving from machine learning (ML) to true artificial intelligence: Lots of data, very flexible models, and powerful priors, and that, since classical ML can handle the first 2, his post deals with the third.
On the path toward AI from today's ML systems, we need learning, generalization, ways to fight the curse of dimensionality, and the ability to disentangle the underlying explanatory factors. Before explaining why non-parametric learning algorithms won't get us to true AI, he gives a nuanced definition of non-parametric. He explains why smoothness, a classical non-parametric approach, won't work on high-dimensionality, and then provides the following insight re: dimensionality:
"If we dig deeper mathematically, it's not the number of dimensions but the number of variations of functions that we learn. In this case, smoothness is about how many ups and downs are present in the curve."
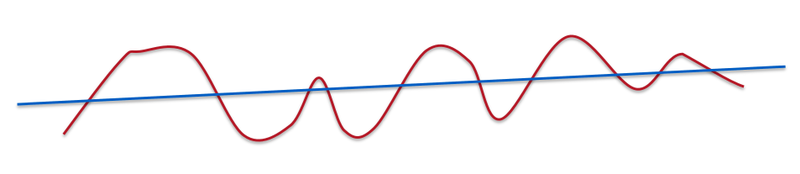
"A line is very smooth. A curve with some ups and downs is less smooth but still smooth."
So, it's clear that smoothness will not beat the curse of dimensionality alone. In fact, smoothness doesn't even apply to modern, complex problems like computer vision or natural language processing. After discussing the downfalls of such competing methods as Gaussian kernels, Boney sets his sights on moving past smoothness, and why that's necessary:
"We want to be non-parametric in the sense that we want the family of functions to grow in flexibility as we get more data. In neural networks, we change the number of hidden units depending on the amount of data."
He notes that in deep learning, 2 priors are used, namely distributed representations and deep architecture.
Why distributed representations?
"With distributed representations, it is possible to represent exponential number of regions with a linear number of parameters. The magic of distributed representation is that it can learn a very complicated function (with many ups and downs) with a low number of examples."
In distributed representations, features are individually and independently meaningful, and they remain so regardless of what the other features are. There maybe some interactions but most features are learned independent of each other. Boney states that neural networks are very good at learning representations capturing the semantic aspects, and that their generalization power is derived from these representations. As a practical exploration of the topic, he recommend's Cristopher Olah's article for some information on distributed representation and Natural Language Processing.
There is a lot of misunderstanding about what depth means.
"Deeper networks does not correspond to a higher capacity. Deeper doesn't mean we can represent more functions. If the function we are trying to learn has a particular characteristic obtained through composition of many operations, then it is much better to approximate these functions with a deep neural network."
Boney then comes full circle. He explains that one of the reasons neural network research was abandon (once again) in the late 90s was because the optimization problem is non-convex. The realization from the work in the 80s and 90s that neural networks have an exponential number of local minima, along with the breakout success of kernel machines, also led to this downfall, as did the fact that networks may get stuck on poor solutions. Recently we have evidence that the issue of non-convexity may be a non-issue, which changes its relationship vis-a-vis neural networks.
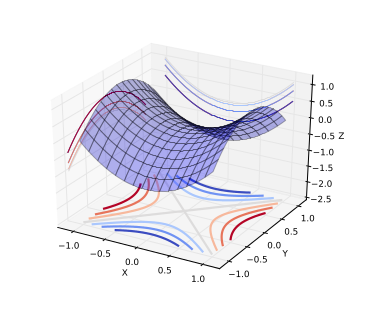
"A saddle point is illustrated in the image above. In a global or local minima, all the directions are going up and in a global or local maxima, all the directions are going down."
Saddle Points.
"Let us consider the optimization problem in low dimensions vs high dimensions. In low dimensions, it is true that there exists lots of local minima. However in high dimensions, local minima are not really the critical points that are the most prevalent in points of interest. When we optimize neural networks or any high dimensional function, for most of the trajectory we optimize, the critical points(the points where the derivative is zero or close to zero) are saddle points. Saddle points, unlike local minima, are easily escapable."
The intuition with the saddle point, is that, for a minima located close to the global minima, all directions should be climbing upward; going further downward is not possible. Local minima exist, but are very close to global minima in terms of objective functions, and theoretical results suggest that some large functions have their probability concentrated between the index (the critical points) and the objective function. The index is the fraction of directions moving downward; for all values of index not 0 or 1 (local minima and maxima, respectively), then it is a saddle point.
Boney goes on to say that there has been empirical validation corroborating this relationship between index and objective function, and that, while there is no proof the results apply to neural network optimization, some evidence suggests that the observed behavior may well correspond to the theoretical results. Stochastic gradient descent, in practice, almost always escapes from surfaces that are not local minima.
This all suggests that local minima may not, in fact, be an issue because of saddle points.
Boney follows his saddle points discussion up by pointing out a few other priors that work with deep distributed representations; human learning, semi-supervised learning, and multi-task learning. He then lists a few related papers on saddle points.
Rinu Boney has written a detailed piece on the motivations for deep learning, including a good discussion on saddle points, all of which is difficult to do justice with a few quotes and some summarization. If you are interested in a deeper discussion of the above points to visit Boney's blog and read the insightful and well-written piece yourself.
Bio: Matthew Mayo is a computer science graduate student currently working on his thesis parallelizing machine learning algorithms. He is also a student of data mining, a data enthusiast, and an aspiring machine learning scientist.
Related:
