Text Mining 101: Topic Modeling
We introduce the concept of topic modelling and explain two methods: Latent Dirichlet Allocation and TextRank. The techniques are ingenious in how they work – try them yourself.
Goutam Nair, IIIT-Hyderabad.
What is Topic Modeling? Why do we need it?
Large amounts of data are collected everyday. As more information becomes available, it becomes difficult to access what we are looking for. So, we need tools and techniques to organize, search and understand vast quantities of information.
Topic modelling provides us with methods to organize, understand and summarize large collections of textual information. It helps in:
- Discovering hidden topical patterns that are present across the collection
- Annotating documents according to these topics
- Using these annotations to organize, search and summarize texts
Topic modelling can be described as a method for finding a group of words (i.e topic) from a collection of documents that best represents the information in the collection. It can also be thought of as a form of text mining – a way to obtain recurring patterns of words in textual material.
There are many techniques that are used to obtain topic models. This post aims to explain the Latent Dirichlet Allocation (LDA): a widely used topic modelling technique and the TextRank process: a graph-based algorithm to extract relevant key phrases.
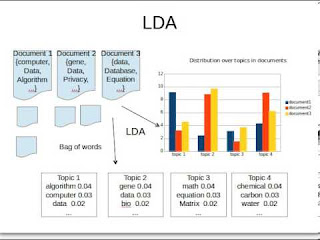
Latent Dirichlet Allocation (LDA)[1]
In the LDA model, each document is viewed as a mixture of topics that are present in the corpus. The model proposes that each word in the document is attributable to one of the document’s topics.
For example, consider the following set of documents as the corpus:
Document 1: I had a peanut butter sandwich for breakfast.
Document 2: I like to eat almonds, peanuts and walnuts.
Document 3: My neighbor got a little dog yesterday.
Document 4: Cats and dogs are mortal enemies.
Document 5: You mustn’t feed peanuts to your dog.
The LDA model discovers the different topics that the documents represent and how much of each topic is present in a document. For example, LDA may produce the following results:
Topic 1: 30% peanuts, 15% almonds, 10% breakfast… (you can interpret that this topic deals with food)
Topic 2: 20% dogs, 10% cats, 5% peanuts… ( you can interpret that this topic deals with pets or animals)
Documents 1 and 2: 100% Topic 1
Documents 3 and 4: 100% Topic 2
Document 5: 70% Topic 1, 30% Topic 2
So, how does LDA perform this process?
Collapsed Gibbs sampling is one way the LDA learns the topics and the topic representations of each document. The procedure is as follows:
- Go through each document and randomly assign each word in the document to one of K topics (K is chosen beforehand)
- This random assignment gives topic representations of all documents and word distributions of all the topics, albeit not very good ones
- So, to improve upon them:
- For each document d, go through each word w and compute:
- p(topic t | document d): proportion of words in document d that are assigned to topic t
- p(word w| topic t): proportion of assignments to topic t, over all documents d, that come from word w
- For each document d, go through each word w and compute:
- Reassign word w a new topic t’, where we choose topic t’ with probability
p(topic t’ | document d) * p(word w | topic t’)
This generative model predicts the probability that topic t’ generated word w
On repeating the last step a large number of times, we reach a steady state where topic assignments are pretty good. These assignments are then used to determine the topic mixtures of each document.
TextRank[2]
Graph-based ranking algorithms are a way of deciding the importance of a vertex within a graph, based on the information derived from the entire graph. The basic idea, implemented by a graph-based ranking model, is that of “voting”.
When one vertex links to another one, it is basically casting a vote for that other vertex. The higher the number of votes that are cast for a vertex, the higher the importance of the vertex. Moreover, the importance of the vertex casting the vote determines how important the vote itself is, and this information is also taken into account by the ranking model. Hence, the score associated with a vertex is determined based on the votes that are cast for it, and the score of the vertices casting these votes.
The score for each vertex, Vi is calculated as:
Here, G = (V, E) is a directed graph with a set of vertices V and a set of edges E. For a given vertex, Vi, In(Vi) denotes the number of inward edges to that vertex and Out(Vi) denotes the number of outward edges from that vertex. d is the damping factor which is set to 0.85, as is done in PageRank[3]. Now to enable the application of this model to natural language texts, we follow the steps:
- Identify text units that best define the task at hand, and add them as vertices in the graph.
- Identify relations that connect such text units, and use these relations to draw edges between vertices in the graph. Edges can be directed or undirected, weighted or unweighted.
- Iterate the graph-based ranking algorithm until convergence.
- Sort vertices based on their final score. Use the values attached to each vertex for ranking / selection decisions.
See Reference 4 below
This method allows us to obtain relevant keyphrases for each document in the collection. So, in order to obtain relevant topics from the entire collection, we apply the same procedure, where each vertex in the graph denotes relevant keyphrases of the document.
References
- D. Blei, A. Ng, M. Jordan. Latent Dirichlet Allocation. Journal of Machine Learning Research, 3: 993-1022, 2003
- R. Mihalcea, P. Tarau. TextRank – bringing order into texts. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP 2004). 2004
- L. Page, S. Brin, R. Motwani, T. Winograd. The PageRank Citation Ranking: Bringing Order to the web. technical report, Stanford University. 1998
- G.Erkan and D.R. Radev, LexRank: Graph-Based Lexical Centrality As Salience in Text Summarization, J. Artificial Intelligence Research, vol. 22, pp. 457-479, 2004
Related: