Deep Learning Reading Group: Deep Networks with Stochastic Depth
An concise overview of a recent paper which introduces a new way to perturb networks during training in order to improve their performance, stochastic depth networks.

Today’s paper is by Gao Huang, Yu Sun, et al. It introduces a new way to perturb networks during training in order to improve their performance. Before I continue, let me first state that this paper is a real pleasure to read; it is concise and extremely well written. It gives an excellent overview of the motivating problems, previous solutions, and Huang and Sun’s new approach. I highly recommended giving it a read!
The authors begin by pointing out that deep neural networks have greater expressive power as compared to shallow networks, that is they can learn more details and better separate similar classes of objects. For example, a shallow network might be able to tell cats from dogs, but a deep network has a better chance of learning to tell Husky from a Malamute. However, deep networks are more difficult to train. Huang and Sun list the following issues that appear when training very deep networks:
- Vanishing Gradients: As the gradient information is backpropagated through the network, it is multiplied by the weights. In a deep network this multiplication is repeated several times with small weights and so the information that reaches the earliest layers is often too little to effectively train the network.
- Diminishing Feature Reuse: This is the same problem as the vanishing gradient, but in the forward direction. Features computed by early layers are washed out by the time they reach the final layers by the many weight multiplications in between.
- Long Training Times: Deeper networks require a longer time to train than shallow networks. Training time scales linearly with the size of the network.
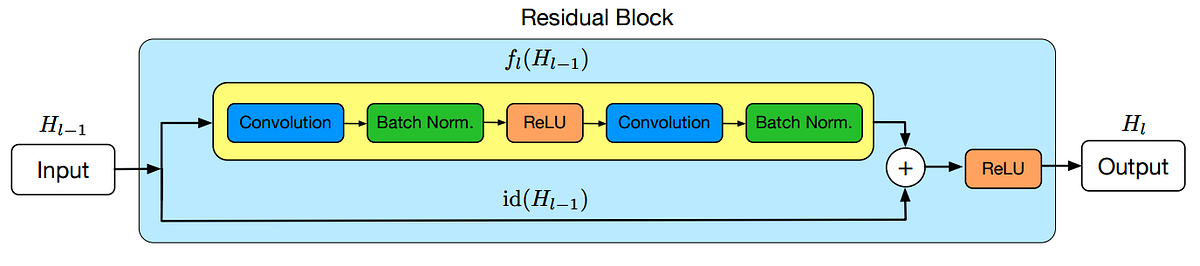
There are many solutions to these problems and the authors propose a new one: Stochastic Depth. In essence what stochastic depth does is randomly bypass layers in the network while training. They construct their network of ResBlocks (see image below) which are a set of convolution layers and a bypass that passes the information from the previous layer through without any change. With stochastic depth, the convolution block is sometimes switched off allowing the information to flow through the layer without being changed, effectively removing the layer from the network. During testing, all layers are left in and the weights are modified by their survival probability. This is very similar to how dropout works, except instead of dropping a single node in a layer the entire layer is dropped!
Stochastic depth adds a new hyper-parameter, p(l), the probability of dropping a layer as a function of its depth. They take p(l) to be linear with it equal to 0.0 for the first layer and 0.5 for the last, although other functions (include a constant) are possible. With this model the expected depth of a network is effectively reduced by 25% with corresponding reductions in training time. The authors also show that it reduces the problems associated with vanishing gradients and diminishing feature use, as expected for a shallower network.
In addition to aiding in training, the trained networks actually perform better than networks trained without stochastic depth! This is because stochastic depth, like dropout, acts as a form of regularization, preventing the network from over training. However, unlike dropout, stochastic depth works with batch normalization making it a very powerful combination.
The authors demonstrate the new architecture on CIFAR-10, CIFAR-100, and the Street View House Number dataset (SVHN). They achieve the lowest published error on CIFAR-10 and CIFAR-100, and second lowest for SVHN. They also test using a very deep network (1202 layers) on CIFAR-10 and find that it produces an even better result, the first time a 1000+ layer network has been shown to further reduce the error on CIFAR-10.
The main idea behind stochastic depth is relatively simple, remove some layers when training to make the network train is if it were shallow, but the results are surprisingly good. The new networks not only train faster, but they perform better as well. Further, the idea is compatible with other methods of improving network training like batch normalization. All in all, stochastic depth is an essentially free improvement when training a deep network. I look forward to giving it a shot in my next model!
Alexander Gude is currently a data scientist at Lab41 working on investigating recommender system algorithms. He holds a BA in physics from University of California, Berkeley, and a PhD in Elementary Particle Physics from University of Minnesota-Twin Cities.
Lab41 is a “challenge lab” where the U.S. Intelligence Community comes together with their counterparts in academia, industry, and In-Q-Tel to tackle big data. It allows participants from diverse backgrounds to gain access to ideas, talent, and technology to explore what works and what doesn’t in data analytics. An open, collaborative environment, Lab41 fosters valuable relationships between participants.
Original. Reposted with permission.
Related: