A Beginner’s Guide To Understanding Convolutional Neural Networks Part 2

Editor's note: You may want to check out Part 1 of this tutorial before reading on.

Introduction

 
In this post, we’ll go into a lot more of the specifics of ConvNets. Disclaimer: Now, I do realize that some of these topics are quite complex and could be made in whole posts by themselves. In an effort to remain concise yet retain comprehensiveness, I will provide links to research papers where the topic is explained in more detail.

Stride and Padding

 
Alright, let’s look back at our good old conv layers. Remember the filters, the receptive fields, the convolving? Good. Now, there are 2 main parameters that we can change to modify the behavior of each layer. After we choose the filter size, we also have to choose the stride and the padding.

Stride controls how the filter convolves around the input volume. In the example we had in part 1, the filter convolves around the input volume by shifting one unit at a time. The amount by which the filter shifts is the stride. In that case, the stride was implicitly set at 1. Stride is normally set in a way so that the output volume is an integer and not a fraction. Let’s look at an example. Let’s imagine a 7 x 7 input volume, a 3 x 3 filter (Disregard the 3rd dimension for simplicity), and a stride of 1. This is the case that we’re accustomed to.

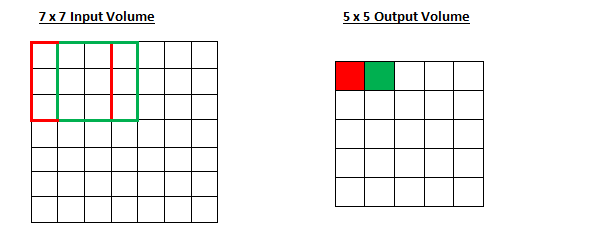
Same old, same old, right? See if you can try to guess what will happen to the output volume as the stride increases to 2.

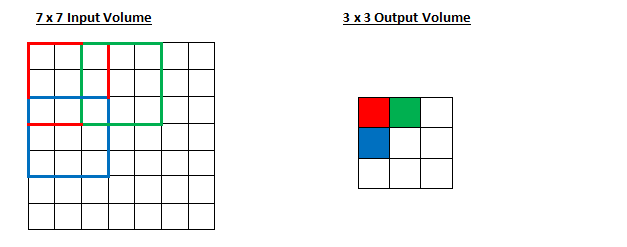
So, as you can see, the receptive field is shifting by 2 units now and the output volume shrinks as well. Notice that if we tried to set our stride to 3, then we’d have issues with spacing and making sure the receptive fields fit on the input volume. Normally, programmers will increase the stride if they want receptive fields to overlap less and if they want smaller spatial dimensions.

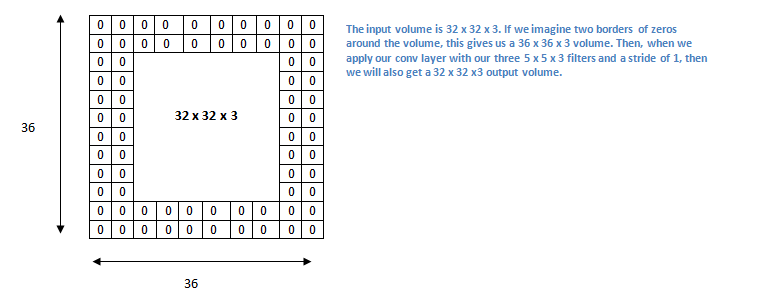
Now, let’s take a look at padding. Before getting into that, let’s think about a scenario. What happens when you apply three 5 x 5 x 3 filters to a 32 x 32 x 3 input volume? The output volume would be 28 x 28 x 3. Notice that the spatial dimensions decrease. As we keep applying conv layers, the size of the volume will decrease faster than we would like. In the early layers of our network, we want to preserve as much information about the original input volume so that we can extract those low level features. Let’s say we want to apply the same conv layer but we want the output volume to remain 32 x 32 x 3. To do this, we can apply a zero padding of size 2 to that layer. Zero padding pads the input volume with zeros around the border. If we think about a zero padding of two, then this would result in a 36 x 36 x 3 input volume.

If you have a stride of 1 and if you set the size of zero padding to

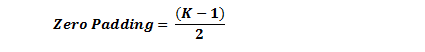
where K is the filter size, then the input and output volume will always have the same spatial dimensions.

The formula for calculating the output size for any given conv layer is

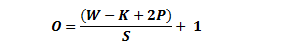
where O is the output height/length, W is the input height/length, K is the filter size, P is the padding, and S is the stride.

Choosing Hyperparameters

 
How do we know how many layers to use, how many conv layers, what are the filter sizes, or the values for stride and padding? These are not trivial questions and there isn’t a set standard that is used by all researchers. This is because the network will largely depend on the type of data that you have. Data can vary by size, complexity of the image, type of image processing task, and more. When looking at your dataset, one way to think about how to choose the hyperparameters is to find the right combination that creates abstractions of the image at a proper scale.

ReLU (Rectified Linear Units) Layers

 
After each conv layer, it is convention to apply a nonlinear layer (or activation layer) immediately afterward.The purpose of this layer is to introduce nonlinearity to a system that basically has just been computing linear operations during the conv layers (just element wise multiplications and summations).In the past, nonlinear functions like tanh and sigmoid were used, but researchers found out that ReLU layers work far better because the network is able to train a lot faster (because of the computational efficiency) without making a significant difference to the accuracy. It also helps to alleviate the vanishing gradient problem, which is the issue where the lower layers of the network train very slowly because the gradient decreases exponentially through the layers (Explaining this might be out of the scope of this post, but see here and here for good descriptions). The ReLU layer applies the function f(x) = max(0, x) to all of the values in the input volume. In basic terms, this layer just changes all the negative activations to 0.This layer increases the nonlinear properties of the model and the overall network without affecting the receptive fields of the conv layer.

Paper by the great Geoffrey Hinton (aka the father of deep learning).