How Bayesian Inference Works
How Bayesian Inference Works
Bayesian inference isn’t magic or mystical; the concepts behind it are completely accessible. In brief, Bayesian inference lets you draw stronger conclusions from your data by folding in what you already know about the answer. Read an in-depth overview here.
Bayesian inference is a way to get sharper predictions from your data. It’s particularly useful when you don’t have as much data as you would like and want to juice every last bit of predictive strength from it.
Although it is sometimes described with reverence, Bayesian inference isn’t magic or mystical. And even though the math under the hood can get dense, the concepts behind it are completely accessible. In brief, Bayesian inference lets you draw stronger conclusions from your data by folding in what you already know about the answer.
Bayesian inference is based on the ideas of Thomas Bayes, a nonconformist Presbyterian minister in London about 300 years ago. He wrote two books, one on theology, and one on probability. His work included his now famous Bayes Theorem in raw form, which has since been applied to the problem of inference, the technical term for educated guessing. The popularity of Bayes' ideas was aided immeasurably by another minister, Richard Price. He saw their significance, refined them and published them. It would be more accurate and historically just to call Bayes' Theorem the Bayes-Price Rule.
Bayesian inference at the movies
Imagine you are at the movies and a fellow moviegoer drops their ticket. You want to get their attention. This is what they look like from behind. You can’t tell their gender, only that they have long hair. Do you call out “Excuse me ma’am!” or “Excuse me sir!” Given what you know about men’s and women’s hairstyles in your area, you might assume that this is a woman. (In this oversimplification, there are only two hair lengths and genders.)
Now consider a variation of the situation where this person is standing in line for the men’s restroom. With this additional piece of information, you would probably assume that this is a man. This use of common sense and background knowledge is something that we do without thinking. Bayesian inference is a way to capture this in math so that we can make more accurate predictions.
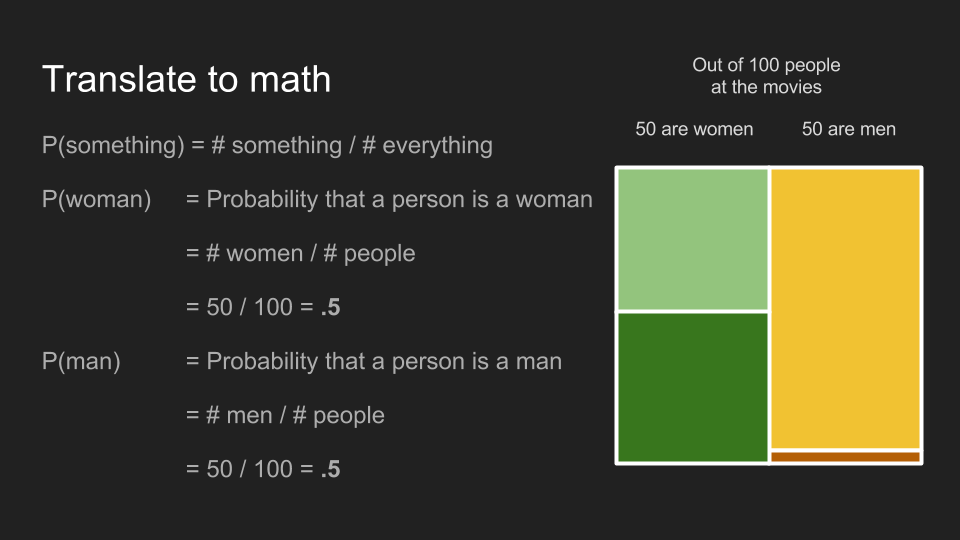
To put numbers to our cinema dilemma, let’s assume that there are about half men and half women at the theater. Out of 100 people, 50 are men, 50 are women. Out of the women, half have long hair (25) and the other 25 have short hair. Out of the men, 48 have short hair and 2 have long hair. Since there are 25 long haired women and 2 long haired men, guessing that the ticket owner is a woman is a safe bet.
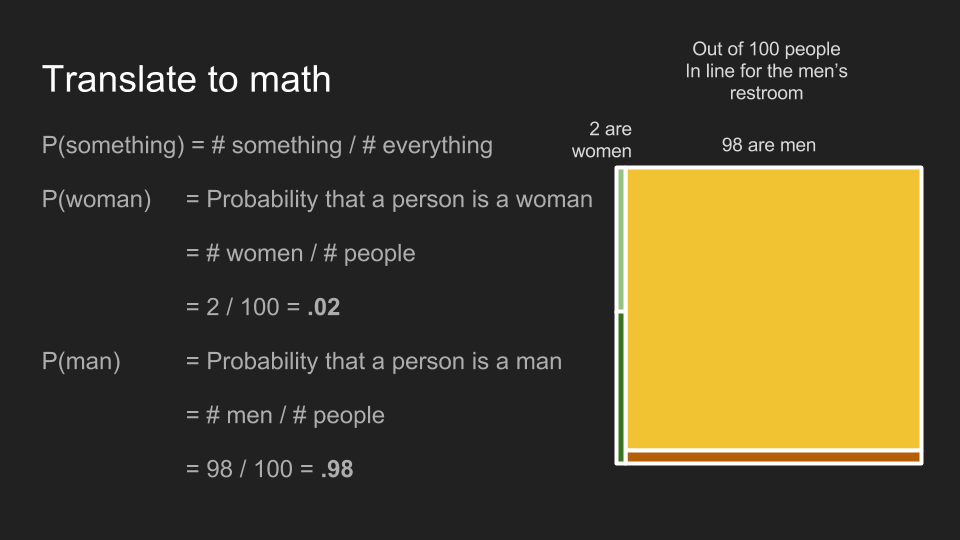
Out of 100 people in the men’s restroom line, however, there are 98 men and two women keeping their partners company. Half the women still have long hair and half have short hair, but here there are just one of each. The proportions of men with long and short hair are the same too, but since there are 98 of them, there are now 94 with short hair and 4 with long. Since there is 1 woman with long hair and four men, now the safe bet is that the ticket owner is a man. This is a concrete example of the principle underlying Bayesian inference. Knowing a key piece of information beforehand - that the ticket owner is in the men’s restroom line - allows us to make a better prediction about them.
To clearly talk about Bayesian inference, it is worth our time to really clearly define our ideas. Unfortunately, this requires using math. We’ll avoid going deeper than we have to, but stick with me for a few more paragraphs and it will pay off. To lay our foundation, we need to quickly mention four concepts: probabilities, conditional probabilities, joint probabilities and marginal probabilities.
Probabilities
The probability of a thing happening is the number of ways that thing can happen divided by the total number of things that can happen. The probability that a moviegoer is a woman is 50 women divided by 100 moviegoers, .5 or 50%. The same holds for men.
The situation in men’s restroom line breaks down to .02 for women, .98 for men.
Conditional probabilities
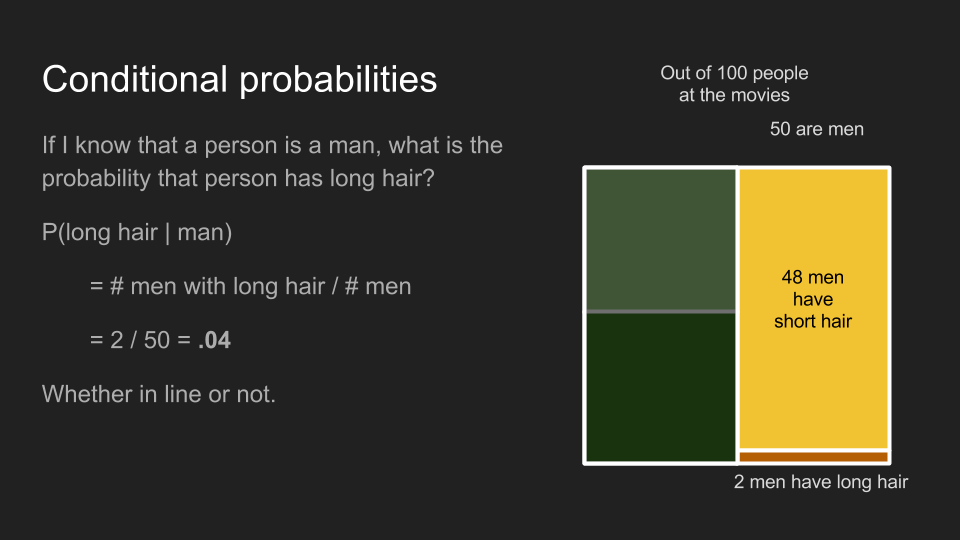
Conditional probabilities answer the question “If I know that a person is a woman, what is the probability that she has long hair?” Conditional probabilities are calculated the same way as straight probabilities, but they just look at a subset of all the examples - those meeting a certain condition. In this case, P(long hair | woman), the conditional probability that someone has long hair, given that she is a woman, is the number of women with long hair, divided by the total number of women. This turns out to be .5, whether we are considering the men’s restroom line, or the theater overall.
By the same math, the conditional probability that someone has long hair, given that he is a man, P(long hair | man), is .04, whether or not they are in line.
An important thing to remember about conditional probabilities is that P(A | B) is not the same as P(B | A). For example, P(cute | puppy) is different than P(puppy | cute). If the thing I’m holding is a puppy, the probability it is cute is very high. If the thing I’m holding is cute, the probability it is a puppy is only medium-low. It might also be kitten, a bunny, a hedgehog or even a tiny human.
Joint probabilities
Joint probabilities are useful for answering the question, “What is the probability that someone is a woman with short hair?” Finding this is a two-step process. First, we focus on the probability that someone is a woman, P(woman). Then, we bring in the probability that someone has short hair, given that she is a woman, P(short hair | woman). Combining these by multiplication gives the joint probability, P(woman with short hair) = P(woman) * P(short hair | woman). Using this approach, we can calculate what we already knew--that P(woman with long hair) among all moviegoers is .25, but that P(woman with long hair) in the men’s restroom line is .01. These are different because P(woman) is different in these two cases.
Similarly, P(man with long hair) is .02 among all moviegoers, but .04 in the men’s restroom line.
Unlike conditional probabilities, joint probabilities don’t care about order. P(A and B) is the same as P(B and A). The probability that I am having milk and a jelly donut is the same as the probability that I am having a jelly donut and milk.
Marginal probabilities
The last stop on our fundamentals tour is marginal probabilities. These are useful for answering the question “What is the probability that someone has long hair?” To find this, we have to add up the probabilities for all the different ways this could happen - the probability of being a man with long hair plus the probability of being a woman with long hair. Adding up those two joint probabilities gives us P(long hair) of .27 for moviegoers generally, but .05 in the men’s restroom line.

 How Bayesian Inference Works
How Bayesian Inference Works