How do you teach physics to machine learning models?
How to integrate physics-based models (these are math-based methods that explain the world around us) into machine learning models to reduce its computational complexity.
By Vegard Flovik, Lead Data Scientist at Axbit AS
In my other posts, I have covered topics such as: Machine learning for anomaly detection and condition monitoring, how machine learning can be used for production optimization, as well as how to avoid common pitfalls of machine learning for time series forecasting.
But did you know that you can also combine machine learning and physics-based modeling? Here, I will describe how it can be done and how we can “teach physics” to machine learning models.
Machine learning versus physics-based modeling
As a physicist, I enjoy making mathematical models to describe the world around us. With sufficient information about the current situation, a well-made physics-based model enables us to understand complex processes and predict future events. Such models have already been applied all across our modern society for vastly different processes, such as predicting the orbits of massive space rockets or the behavior of nano-sized objects which are at the heart of modern electronics.
The ability to make predictions is also one of the important applications of machine learning (ML). A common key question is how you choose between a physics-based model and a data-driven ML model. The answer depends on what problem you are trying to solve. In this setting, there are two main classes of problems:
1) We have no direct theoretical knowledge about the system, but we have a lot of experimental data on how it behaves.
If for instance, you have no direct knowledge about the behavior of a system, you cannot formulate any mathematical model to describe it and make accurate predictions.
Luckily, all is not lost. If you have a lot of example outcomes, you could use an ML-based model. Given enough example outcomes (the training data), an ML model should be able to learn any underlying pattern between the information you have about the system (the input variables) and the outcome you would like to predict (the output variables).
An example of this could be predicting the housing prices of a city. If you have enough examples of the selling prices of similar houses in the same area, you should be able to make a fair prediction of the price for a house that is put up for sale.
2) We have a good understanding of the system, and we are also able to describe it mathematically.
If a problem can be well described using a physics-based model, this approach will often be a good solution.
This does not mean that machine learning is useless for any problem that can be described using physics-based modeling. On the contrary, combining physics with machine learning in a hybrid modeling scheme is a very exciting prospect. So exciting, in fact, that it is being studied in-depth. In connection with my work, I have recently been deep-diving into this intersection between machine learning and physics-based modeling myself.
Hybrid analytics: combining machine learning and physics-based modeling
Even if a system, at least in principle, can be described using a physics-based model, this does not mean that a machine learning approach would not work. The ability of ML models to learn from experience means they can also learn physics: Given enough examples of how a physical system behaves, the ML model can learn this behavior and make accurate predictions.
This ability of learning physics through experience rather than through mathematical equations is familiar to many of us, although we may not realize it. For instance, if you have ever played football, you probably would have tried to make the perfect shot. And to do that, you had to predict the path of the ball accurately. This is a somewhat complicated physics problem that includes several variables such as the force at which you kick the ball, the angle of your foot, the weight of the ball, the air resistance, the friction of the grass, and so on and so forth.
However, when a football player kicks the ball it is not a result of complicated physics calculations he has performed within a fraction of a second. Rather, he has learned the right movements from experience and obtained a gut feeling about making the perfect shot.
(Illustration by: Deviant Art)
The fact that ML models — or algorithms — learn from experience in principle resembles the way humans learn. A class of ML models called artificial neural networks are computing systems inspired by how the brain processes information and learns from experience.
This ability to learn from experience also inspired my colleagues and me to try teaching physics to ML models: Rather than using mathematical equations, we train our model by showing it examples of the input variables and the correct solution.
Why use machine learning when we already have physics-based models?
An important question is why should we implement an ML-based approach when we have a physics-based model that is able to describe the system in question.
One of the key aspects is the computational cost of the model: We might be able to describe the system in detail using a physics-based model. But solving this model could be complicated and time-consuming. Thus, a physics-based approach might break down if we aim for a model that can make real-time predictions on live data.
In this case, a simpler ML-based model could be an option. The computational complexity of an ML model is mainly seen in the training phase. Once the model has finished training, making predictions on new data is straightforward. This is where the hybrid approach of combining machine learning and physics-based modeling becomes highly interesting.
Virtual flow metering through a hybrid modeling scheme
We have, for instance, considered this approach for the specific task of virtual flow metering in an oil well, as illustrated in the figure below. Several sensors can provide measurements of temperature and pressure downhole the well P_dh, T_dh as well as upstream P_uc, T_uc, and downstream P_dc, T_dc of the well choke. The problem we want to solve is how the flow of oil, gas, and water depends on these measurements: i.e., the function that describes the multiphase flow rates:
![]()
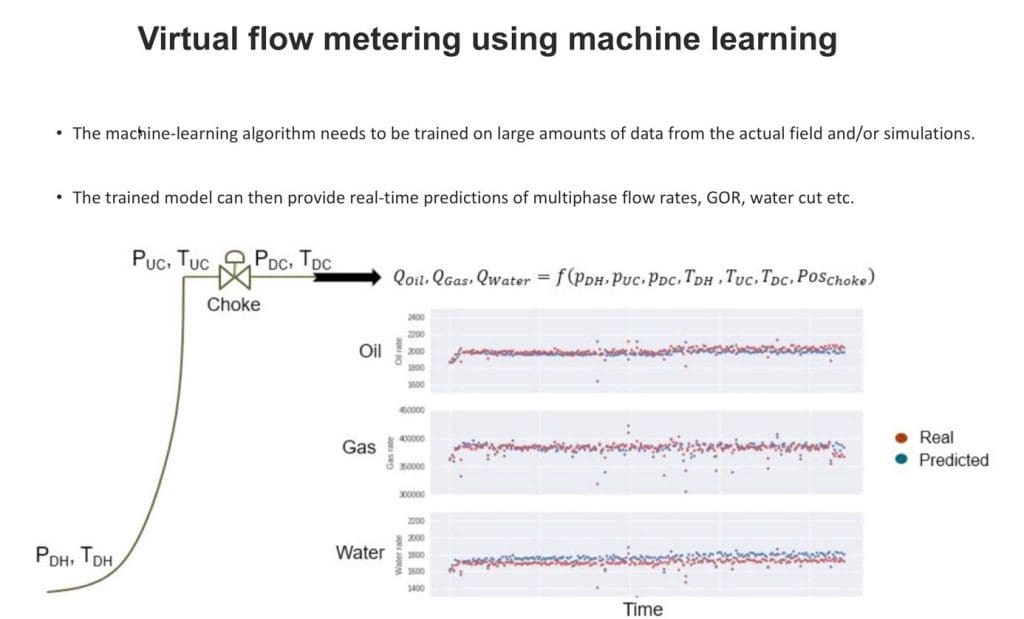
This is a complex modeling task to perform, but using state of the art simulator tools, we can do it with a high degree of accuracy.
The model captures both the thermodynamics and fluid dynamics of the multiphase flow of oil, gas, and, water from the production well. Utilizing this, we can generate lots of simulated training data for the ML model and combine them with real-life data from the physical well.
The advantage of this approach is that we can perform all the computationally demanding parts off-line, where making fast real-time predictions is not an issue. By generating large amounts of training data from the physics-based model, we can teach the ML model the physics of the problem.
A trained ML model can use just the sensor measurements from the physical well, i.e., pressures and temperatures, to predict the oil, gas, and water rates simultaneously. More importantly, it can make these predictions within a fraction of a second, making it an ideal application for running on real-time data from the production wells.
This approach allows us to implement virtual multiphase flow meters for all wells on a production facility. I have no doubt it will become an extremely valuable tool for both monitoring and production optimization purposes.
What other areas do you think will benefit from machine learning?
In the future, I believe machine learning will be used in many more ways than we are even able to imagine today. What impact do you think it will have on the various industries? I would love to hear your thoughts in the comments below.
Bio: Vegard Flovik is a Lead Data Scientist at Axbit As.
Original. Reposted with permission.
Related:
