By Diego Lopez Yse, Data Scientist
I decided to write this introduction to probability distributions with one clear purpose in mind: explain why do we use them, and apply real-life examples. When learning probability, I got tired of hearing about coins tosses, card games and numbered balls. Unless you only love to gamble (which is not my case), you need to get really pragmatic to apply concepts about probability to solve other problems rather than what are the odds of winning the lottery. But before diving into pragmatism (and this will be our first conflict), we need to go through some conceptual matters. This article describes why do we care about probability, and will help you develop some key terminology that we’ll need to understand how to apply it to our real-life problems.
What is probability, and why do we even care?
Probability is about interpreting and understanding the random events of life, and since we live in absolute randomness (even if we try to believe we don’t), its usefulness becomes quite clear. Probability is the long-term chance that a certain outcome will occur from some random process. It basically tells you how often different kinds of events will happen.
Some real life examples of the use of probabilities are:
- Finance: By estimating the chance that a given financial asset will fall between or within a specific range, it’s possible to develop trading strategies to capture that predicted outcome.
- Weather forecast: Meteorologists can’t predict exactly what the weather will be, so they use tools and instruments to determine the likelihood that it will rain, snow or hail. They also examine historical data bases to estimate high and low temperatures and probable weather patterns for that day or week.
- Insurance: Probability plays an important role in analyzing insurance policies to determine which plans are best for customers and what deductible amounts they need.
- Sports: Athletes and coaches use probability to determine the best sports strategies for games and competitions. Companies like BWin have made a business out of this and you can even bet using different strategies.
- Advertisement: Probability is used to estimate potential customers that will be more likely to react positively to specific campaigns, based on their consumption patterns.
Numerically speaking, a probability is a number that ranges from 0 (meaning there is no way an event is going to happen) to 1 (which means the event will happen for sure), and if you take all the possible outcomes and add them up, you sum to 1. The bigger the value of the probability, the more likely the event is to occur.
So for example, you’d say that the probability of rain tomorrow is 40% (stated as “P(rain)=0,4”), or the probability of a car theft in a particular region is 2% (defined as “P(car theft)=0,02”). In the first case you’re interested in the variable “rain”, and in the second in the variable “car theft”. These variables, as well as any other that is a result of a random process, are referred to as “random variables”.
A random variable is a variable that is subject to random variations so that it can take on multiple different values, each with an associated probability.
It doesn’t have a specific value, but rather a collection of potential values. After a measurement is taken and the specific value is revealed, then the random variable ceases to be a random variable and becomes data.
Different probabilities present different complexities when trying to estimate them. Usually, past data is used as a proxy of what’s likely to happen, but this is not always applicable (e.g. for new events with no history), or can be misleading when extreme events occur: think about the Fukushima accident in 2011, where the height of the tsunami was underestimated because probability calculations resulted in a considerably smaller earthquake than the one that actually struck. There are also different approaches to calculate probabilities (e.g. using computer simulations, or collecting data and calculating the percentage of time that an event occurred), but all of them are as good as the data you use to feed them.
Probability Distributions
A probability distribution is a list of all of the possible outcomes of a random variable, along with its corresponding probability values. A probability distribution links each outcome of a random variable or process with its probability of occurrence. For example, if you take blood samples from different individuals in a given place, you can calculate the probability distribution of their blood types:

What you are doing here is counting the number of individuals with different blood types, and then divide each blood type group by the total amount of individuals. That way you get the probability of each blood type.
In this case, blood type is the random variable. The probability distribution shows that individuals with blood type “A” have the highest probability of occurrence, as opposed to people with blood type “AB”, that have the lowest one. Also, if you sum up the different probabilities, you get 1. How do you do this? Simple: you define the random variable you want to analyze (in this example is “blood type”), you set the categories you want to count (“O”, “A”, “B” and “AB”), and you count the number of occurrences in each category. Then you either work with that absolute number (e.g. 150 cases of blood type “A”), or you divide it by the total number of cases (making it a percentage of total, like in our example).
But there is a trick here. When you estimate the probability distribution of a random variable (like blood type, or any other), what you’re actually doing is using data that represents only a part of the real behavior of that random variable you’re analyzing. You are not looking at all the possible data values (which in probabilistic terms is defined as “population”), since you only obtained data from a subset of it (which is referred to as “sample”) in a given point in time and space.
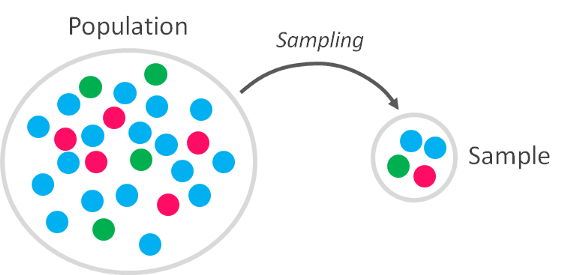
Since the value of a random variable changes within the context in which they are analyzed, each time you calculate the probability of that outcome you need to take a subset of data (sampling), and since you’re doing this in particular conditions, it means that if you repeat your analysis again in the future you might get different results (due to the variable randomness). Some values will result more likely than others today, but others may be more likely in another time. This way, the sample is a representation of the population we want to analyze, but it will never be 100% identical to it.
What if we measure all possible outcomes of the random variable we’re interested in, everywhere and all the time, and capture the real behavior of it?
My answer is that, if you can do that, then your problem is solved: you can calculate the probability distribution of all outcomes with absolute certainty, understand how the random variable you’re interested in behaves and even predict it with better accuracy. Nevertheless, most of the times (if not always) it would extremely expensive (and sometimes impossible) to reach the whole population of data that you’re interested in.
Take an example: suppose we perform a survey on 2.000 adults to estimate the percentage of adults who favor death penalty in Germany (+80 million habitats). If we get that 60% (1.200) of the surveyed people are in favor, can we conclude that 60% of Germans think the same way? Obviously not. We need to either build a conclusion from our sample using probability (and statistical) tools, or reach the whole population of data and forget about those annoying probability concepts. Well, can you imagine surveying 80 million people?
How can you describe the real behavior of the random variables you’re analyzing if you have limited results and also their behavior is random?
OK, now we know that we want to draw reliable conclusions about the “real behavior” of a random variable (not just in our sample, but also outside of it) on the basis of what we’ve discovered in our analysis (which is limited to the sample we could get). Is there a way to generalize those results in a way that they are representative?
The answer is yes, and this generalization holds the secret to prediction. If you can generalize to the population the results from your sample on specific random variables, then you can predict how those random variables will behave.
The power of Prediction
There are probability distributions models that help you predict outcomes in specific situations. When certain conditions are met, these probability distributions models assist you to calculate each outcome probability, the long-term average outcomes, and estimate the variability in the results of random variables, without the need to have all the actual outcomes of the random variables you’re interested in.
This means that there is a way of generalizing the results of your limited analysis on random variables to broader behaviors, which will help you to save time, money and reach more confident results. Lots of probability distributions models exist for different situations, and the key point is that you have to select the right one that fits your data and helps you explain what you’re trying to understand.
In simple terms, a probability distribution model is a guide you use to fit a random variable in order to generalize its behavior. These models have a mathematical background, and can be very picky. For them to work properly, the random variable you are trying to fit in must meet different assumptions so that the outcomes of the model have the correct probabilities, and also so that you can test and validate the model against real data from the random variable.
Types of Random Variables
So far we’ve been talking about random variables, but there are different types of random variables. Hmm…interesting, but why do we care about it? Because the type of random variable is a key parameter when defining which probability distribution model you should choose.
There are 2 major types of random variables:
1. Discrete random variables: are the ones that have either a finite or countably number of possible outcomes. You calculate its value by counting.
For example, think about the “number of births in a place in a given year”. This is a discrete random variable, since the outcome might be 0,1,2…999, or any other. You get the value of the variable by counting. In a discrete random variable, if you pick any two consecutive outcomes you can’t get an outcome that’s in between.
2. Continuous random variables: has an uncountable infinite number of possible values. You calculate its value by measuring.
Consider the “time it takes an algorithm to run a task”. Time is often rounded up to convenient intervals, like seconds or milliseconds, but the truth is it’s actually a continuum: it could take 1.6666666… seconds to run. Weights, temperatures, prices, they are all continuous random variables.
In probabilistic terms, discrete and continuous random variables are 2 different creatures that should be treated completely separate, and there are different probability distributions model for each one of them. This means that if you’re dealing with a discrete random variable (e.g. number of cell phones by house owner in a given area), you need to select a probability distribution model that handles discrete random variables (you can’t choose one that deals only with continuous random variables).
Dancing with Statistics
Probability has a close relationship with statistics. In fact, they are so intimately linked that is almost impossible to talk about one without mentioning the other. Statistics are applied to sets of data to determine factors or attributes that characterize them, in order to gain information about them: it is a discipline concerned with the collection and interpretation of quantitative data, which blended with probability gives us the possibility to make predictions about outcomes.
A statistic is a numerical measure that describes some property of the data, and believe it or not, we use them every day. For example, when you check the average scoring rate of a soccer player (in statistical terms called “the mean”), or the most popular newborn boy name in your country in a given period (in statistical terms called “the mode”), you are using statistics.
The part of statistics that only describes data is called “descriptive statistics”, while the part of statistics that allows you to make predictions is called “inferential statistics”.
Means, modes, medians, variances, standard deviations, these are some of the statistics you can use to describe your data, and just like in probability, unless you have access to all available data (the population), a “statistic” is always obtained from a sample: if you could get it from the population, you’d call it a “parameter”. From this information it’s possible to build predictive models and determine the probability of certain outcomes before the outcome is actually realized. This way, you can use statistics to work out the probability that a certain event will occur.
For instance, if you want to know the chance that your holiday plane will crash (sorry for the dark example), you can think of how many planes usually crash within a year, and since that number is very small, you deduce that the probability of your plane crashing is small too. Here, you’re actually applying statistics by calculating certain parameter like the number of crushed planes divided by the total number of flights. Or you can use statistics for example with a sample of data from woman in a given town to make inferences about a larger population of women (with a similar age range), that are living in larger areas like a city.
Once again, we do this because estimating or inferring parameters is easier than dealing with real life. We need statistics to describe our available data, understand it, and then blend it with probability to guess how the “real” (non-available) data behaves.
That is because a statistic is observable, being computed from the observations, while a population parameter, being an abstraction, is not observable and must be estimated (unless you have complete access to it).
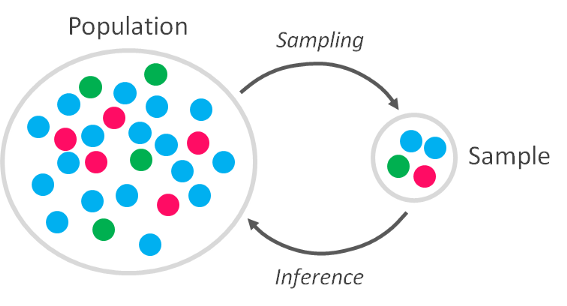
So, how do we infer?
The possible outcomes of a random variable can be estimated using statistics and probability in different ways:
- Calculating the value of a single outcome of a random variable (like the exact value of a stock price mean), called point estimation.
- Estimating an interval or range of possible outcomes of a random variable (e.g. the different values of the stock price mean), called interval estimation.
- Testing the validity of a statement (that is relative to a population parameter), by using statistical methods to confirm or reject that statement. This statement is called a hypothesis and the statistical tests used for this purpose are called statistical hypothesis tests.
These methods lean on the concept of probability distributions, since you need to use probability distribution models to make inferences and generalize your conclusions.
Final thoughts
Probability distributions help to model our world, enabling us to obtain estimates of the probability that a certain event may occur, or estimate the variability of occurrence. They are a common way to describe, and possibly predict, the probability of an event.
The main challenge is to define the characteristics of the variables whose behaviour we are trying to describe, since it’s necessary to identify what distribution should be applied to a model a particular process.
The identification of the right distribution will allow a proper application of a model (for instance, the standardized normal distribution) that would easily predict the probability of a given event.
Interested in these topics? Follow me on Linkedin or Twitter
Bio: Diego Lopez Yse is an experienced professional with a solid international background acquired in different industries (capital markets, biotechnology, software, consultancy, government, agriculture). Always a team member. Skilled in Business Management, Analytics, Finance, Risk, Project Management and Commercial Operations. MS in Data Science and Corporate Finance.
Original. Reposted with permission.
Related:
- Overview of data distributions
- Exploratory Data Analysis on Steroids
- Time Complexity: How to measure the efficiency of algorithms

