Math 2.0: The Fundamental Importance of Machine Learning
Machine learning is not just another way to program computers; it represents a fundamental shift in the way we understand the world. It is Math 2.0.
By Dr. Claus Horn, Researcher and Lecturer in AI

Some people, especially during the current data science hype, see machine learning as just another algorithm. It is part of digitization and helps us automate things, and that’s all. Unfortunately, this interpretation completely misses the main point. Machine learning is not just another way to program computers; it represents a fundamental shift in the way we understand the world. It is Math 2.0.
Scientific theories help us to understand the world by building models of it. Their usefulness stems from the fact that they allow us to make predictions about the future. Until this point in history, our most sophisticated models of the world were written in the language of mathematics (Math 1.0). This is changing now. The coming generation of scientific models will be machine learning models (probably neural networks): Math 2.0.
The reason is that machine learning models allow us to describe phenomena of a higher level of complexity. The functional relationships we can describe in a mathematical theory are very limited, compared to e.g. the function which maps ten thousand pixel values to the concept of a dog or a cat, which is what modern deep learning does very well.
Back in 2003, during my Ph.D. in physics, we were looking for signs of new types of elementary particles scanning through a few petabytes of data recorded at DESY, the German center for high energy physics (which at the time was one of the biggest datasets in the world, Google had been founded only five years earlier).
We found the normal process of applying independent selections on our observation variables a bit tedious since after changing the cut on one variable, we had to revisit all the others. So we thought: Can we automate this? And indeed, a simple algorithm that we came up with allowed us to optimize our selection automatically. We later found out that computer scientists had a term for what we were doing: They called it machine learning.
Quite quickly, it became apparent that this new approach meant we needed to adjust our scientific workflow. Instead of using all our physics knowledge to increase the signal to background ratio, it was much better to do only the minimal cleanup cuts and let the algorithm do the work. Later, with the advent of deep learning, researchers at CERN realized that even the reconstruction of physical quantities is counterproductive. Just given the raw measurements, deep learning is able to outperform any physicist making selections by hand (see figure below). So Math 2.0 lets us see particles that models based on Math 1.0 cannot see.
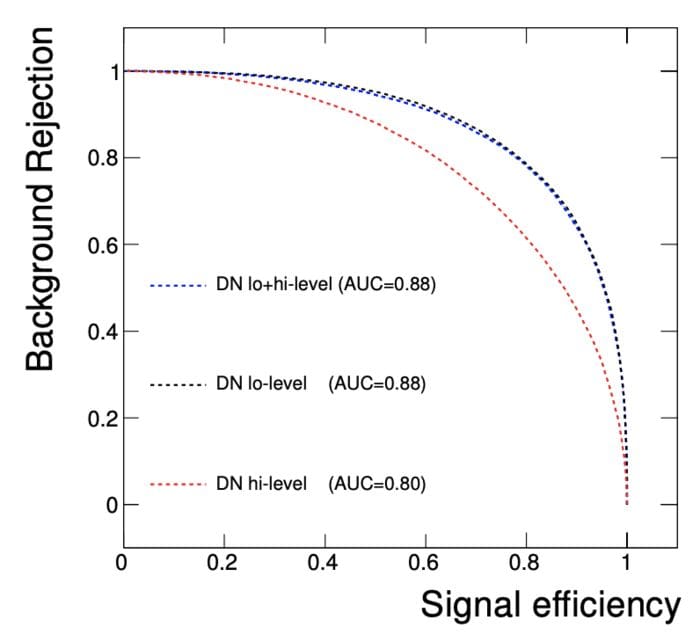
Figure 1: Comparison of the performance of deep learning algorithms based on low-level features alone (black) and high-level features usually used by physicists (red). (Figure taken from the 2014 Nature paper of reference 1.)
People have been wondering why it is that most physical models are very simple, for the most part only involving polynomials of degree three or less. Maybe the reason is that we only see what we can speak about.
What happened before in physics is now happening in other fields: A given sequence of amino acids always folds in the same way. There is a lot of regularity there! In fact, it is a protein’s structure that defines its function. However, we cannot produce a mathematical function to describe this relationship. But we can build a machine learning model which does. Building such a model is such an important milestone that there is speculation about whether AlphaFold, how this particular model is called, may be worth a Nobel Prize.
Because Math 2.0 lets us describe much more complex relationships than Math 1.0, the next decade will likely see a transformation of biology. Digital biology will be written in the language of Math 2.0. And there will be numerous opportunities in other scientific fields with more complex relationships, like social sciences.
Therefore, speaking the language of Math 2.0 should be a core component of every academic curriculum and a basic competency of every student, especially in the sciences.
Of course, there is more to a scientific theory than just mathematics. The main difficulty is finding the right concepts and quantities to describe a given range of phenomena. And that will not change. But mathematics does more for us than building models and deriving predictions. It also allows us to calculate and derive new simplified insights (through algebra) and answer questions about the dynamics of a system (through calculus).
We are still at the beginning of the Math 2.0 revolution, but I predict that, similarly to the development of mathematics, we will see the emergence of a new field that will study systems of machine learning models and how they can be constructed, automatically optimize themselves, and be used to derive new insights enabling us to see the world in a new light.
These developments will result in the next level of scientific computing and give us a new way of doing science, thanks to Math 2.0.
References:
- Baldi, P., Sadowski, P. & Whiteson, D. Searching for exotic particles in high-energy physics with deep learning. Nat Commun5, 4308 (2014). https://doi.org/10.1038/ncomms5308
Bio: Dr. Claus Horn is a Researcher and Lecturer in AI, convinced that the highest potential for advancing the human condition in the 21st century lies at the intersection of artificial intelligence and life sciences.
Original. Reposted with permission.
Related:
- How Machine Learning Leverages Linear Algebra to Solve Data Problems
- Antifragility and Machine Learning
- Linear Algebra for Natural Language Processing
