The Bias-Variance Trade-off
Understanding how these prediction errors work and how they can be used will help you build models that are not only accurate and perform well - but also avoid overfitting and underfitting.
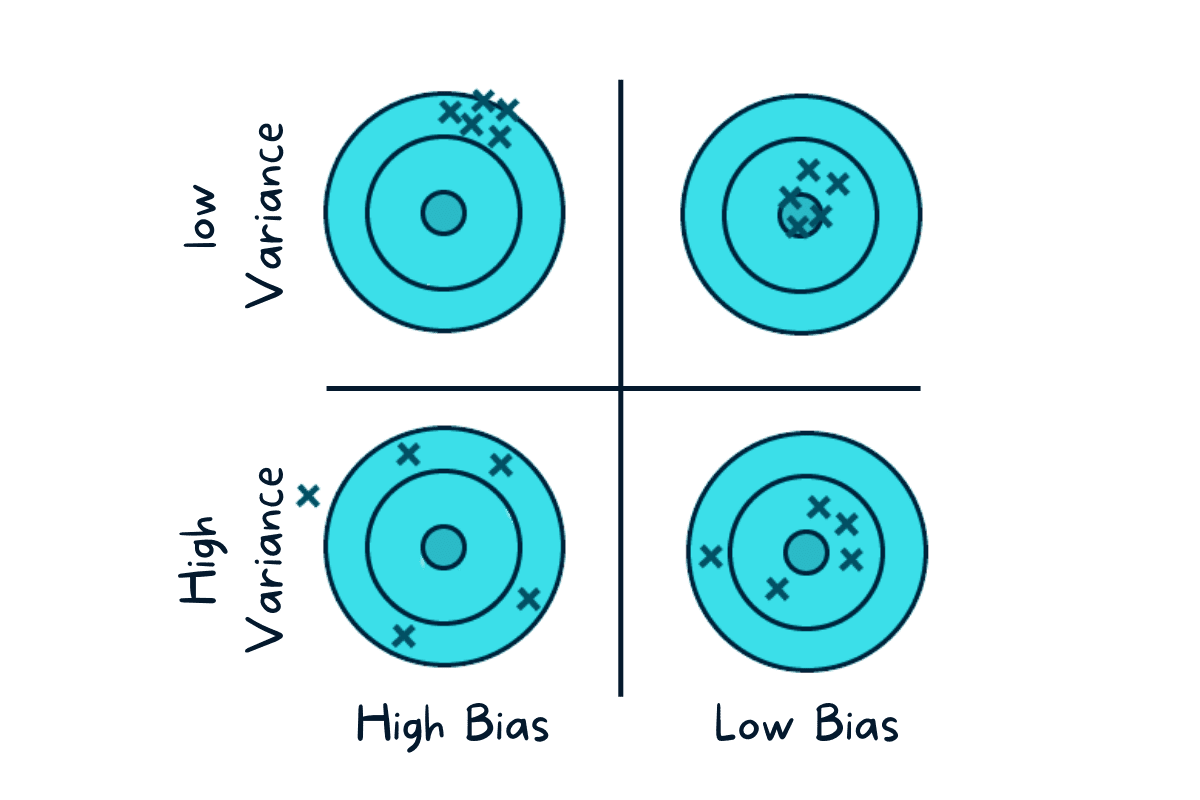
Image by Editor
You may have heard of the Bias-Variance tradeoff before and thought, “huh?” Or perhaps you have never heard of it at all and are thinking, “what the hell is that?”
Either way, the Bias-Variance tradeoff is an important concept in supervised machine learning and predictive modeling. When you want to train a predictive model, there are various supervised machine learning models that you can choose from. Each of these are unique with similarities - however the biggest difference is their level of Bias and Variance.
When it comes to model predictions, you will focus on prediction errors. Bias and Variance are types of prediction errors which are widely used in many industries. When it comes to predictive modeling, there is a tradeoff between minimizing bias and variance in the model.
Understanding how these prediction errors work and how they can be used will help you build models that are not only accurate and perform well - but also avoid overfitting and underfitting.
Let's start off with the definitions of the two.
What is Bias?
Bias is something that causes a skew in the result of a model due to its limited flexibility to learn signals from a dataset. It is the difference between the average prediction of our model and the correct value which we are trying to predict.
When you come across a model that has a high bias, this means that the model has not learned well on the training data. This further leads to a high error on the training and test data as the model has become oversimplified from not learning anything about the features, data points, etc.
What is Variance?
Variance is the changes in the model when it uses different sets of the training data set. It tells us the spread of our data and its sensitivity when using the different sets.
When you come across a model that has high variance, this means that the model has learned well on the training data, however it will not be able to generalize well on unseen or test data. Therefore, this will lead to having a high error rate on test data and causing overfitting.
So what is the Trade-off?
When it comes to machine learning models, it’s also about finding the happy medium.
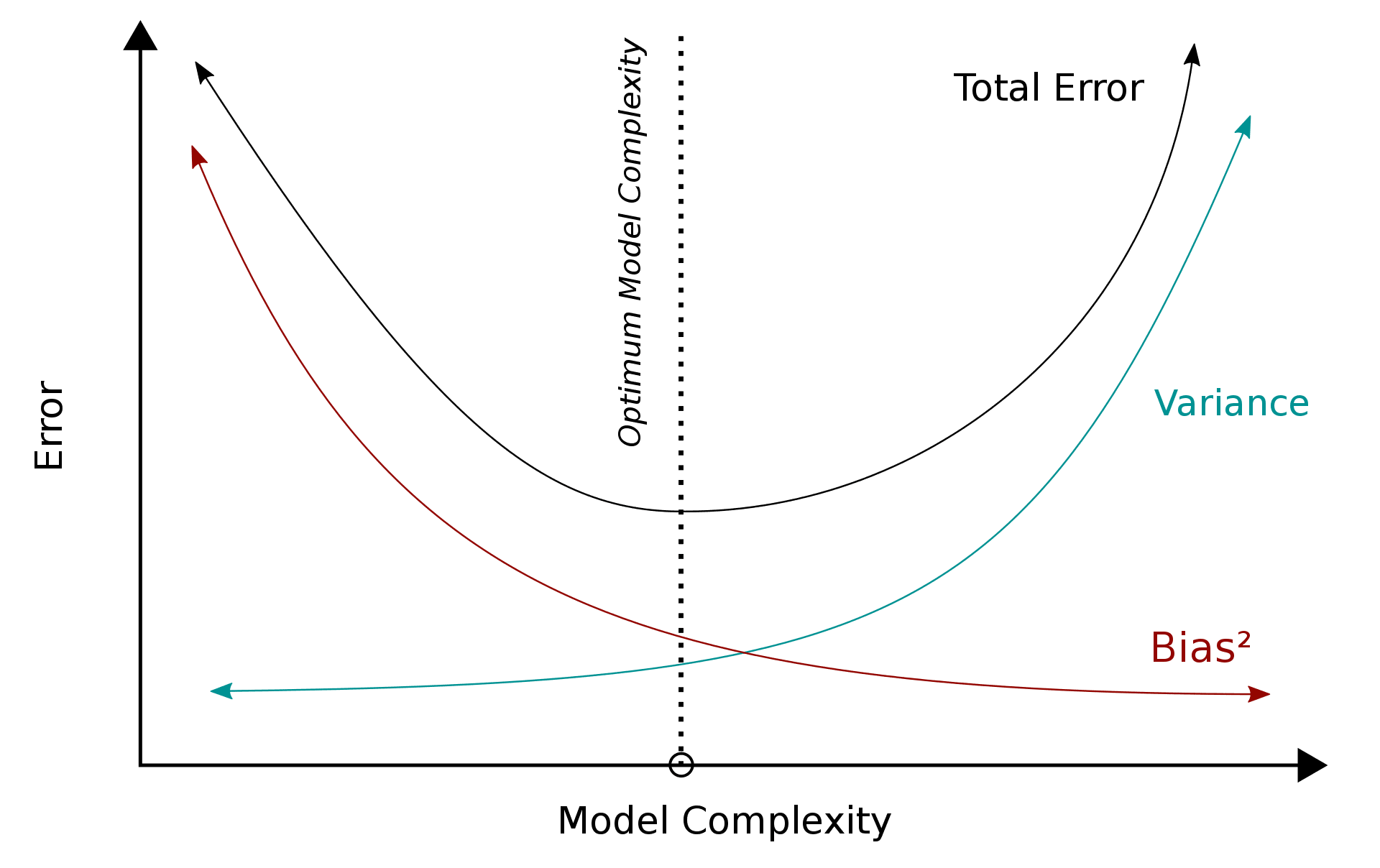
If a model is way too simple - this could lead to high bias and low variance. If a model is too complex with a number of parameters - this could lead to high variance and low bias. Therefore, our aim here is to find the perfect point in which overfitting or underfitting does not occur.
A low variance model is normally less complex and holds a simple structure - however there is a risk of high bias. Examples of these are Naive Bayes, Regression and more. This leads to underfitting as the model is unable to identify the signals in the data to be able to make predictions on unseen data.
A low bias model is normally more complex and holds a more flexible structure - however there is a risk of high variance. Examples of these are Decision Trees, Nearest Neighbors and more. When a model is too complex, this leads to overfitting as the model has memorized the noise in the data, rather than the signals.
If you would like to know more about how to avoid overfitting, signals and noise, click on this link.
This is where the Trade-off comes into play. We need to find that happy medium between Bias and Variance to minimize the total error. Let’s dive into Total Error.
The Math behind it
Let's start off with a simple formula where what we are trying to predict is ‘Y’ and the other covariates are ‘X’. The relationship between the two can be defined as:
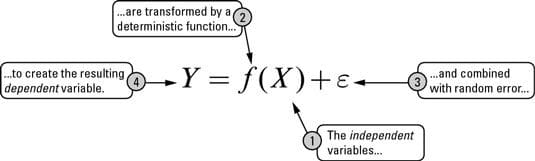
‘e’ refers to the error term.
The expected squared error at a point x can then be defined as:
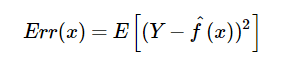
Which then produces:
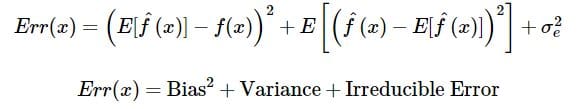
This can be defined better into:
Total Error = Bias2 + Variance + Irreducible Error
Irreducible Error means the ‘noise’ that cannot be reduced in modeling - a way to reduce it would be through data cleaning.
Source: Wikipedia
However, it is important to note that regardless of how amazing your model is, data will always have an element of irreducible error that cannot be removed. When you find that optimum balance between Bias and Variance, your model will never overfit or underfit.
Conclusion
Hopefully in this article you have a better understanding of what Bias is, what Variance is and how they affect predictive modeling. You will have also understood what the trade-off is between the two and why it is important to find that happy medium to produce the best performing model that will not overfit or underfit - with a little bit of math behind it.
Nisha Arya is a Data Scientist and Freelance Technical Writer. She is particularly interested in providing Data Science career advice or tutorials and theory based knowledge around Data Science. She also wishes to explore the different ways Artificial Intelligence is/can benefit the longevity of human life. A keen learner, seeking to broaden her tech knowledge and writing skills, whilst helping guide others.
