5 Statistical Paradoxes Data Scientists Should Know
Knowing these 5 statistical paradoxes is essential for data scientists to improve their analyses and machine learning models.

Image by Author
Introduction
As data scientists, we rely on statistical analysis to crawl information from the data about the relationships between different variables to answer questions, which will help businesses and individuals to make the right decisions. However, some statistical phenomena can be counterintuitive, possibly leading to paradoxes and biases in our analysis, which will ruin our analysis.
These paradoxes I will explain to you are easy to understand and do not include complex formulas.
In this article, we will explore 5 statistical paradoxes data scientists should be aware of: the accuracy paradox, the False Positive Paradox, Gambler’s Fallacy, Simpson’s Paradox, and Berkson’s paradox.
Each of these paradoxes may be the potential reason for getting the unreliable result of your analysis.

Image by Author
We will discuss the definitions of these paradoxes and real-life examples to illustrate how these paradoxes can happen in real-world data analysis. Understanding these paradoxes will help you remove possible roadblocks to reliable statistical analysis.
So, without further ado, let’s dive into the world of paradoxes with Accuracy Paradox.
Accuracy Paradox
Image by Author
Accuracy shows that accuracy is not a good evaluation metric when it comes to classifying.
Suppose you are analyzing a dataset that contains 1000 patient metrics. You want to catch a rare kind of disease, which will eventually be shown itself in 5% of the population. So overall, you have to find 50 people in 1000.
Even if you always say that the people do not have a disease, your accuracy will be 95%. And your model can't catch a single sick person in this cluster. (0/50)
Digits Data Set
Let’s explain this by giving an example from well-known digits data set.
This data set contains hand-written numbers from 0 to 9.

Image by Author
It is a simple multilabel classification task, but it can also be interpreted as image recognition since the numbers are presented as images.
Now we will load these data sets and reshape the data set to apply the machine learning model. I am skipping explaining these parts because you might also be familiar with this part. If not, try searching digit data set or MNIST data set. MNIST data set also contains the same kind of data, but the shape is bigger than this one.
Alright, let’s continue.
Now we try to predict if the number is 6 or not. To do that, we will define a classifier that predicts not 6. Let’s look at the cross-validation score of this classifier.
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.base import BaseEstimator
import numpy as np
digits = datasets.load_digits()
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
x_train, x_test, y_train, y_test = train_test_split(
data, digits.target, test_size=0.5, shuffle=False
)
y_train_6 = y_train == 6
from sklearn.base import BaseEstimator
class DumbClassifier(BaseEstimator):
def fit(self, X, y=None):
pass
def predict(self, X):
return np.zeros((len(X), 1), dtype=bool)
dumb_clf = DumbClassifier()
cross_val_score(dumb_clf, x_train, y_train_6, cv=3, scoring="accuracy")
Here the results will be as the following.

What does it mean? That means even if you create an estimator that will never estimate 6 and you put that in your model, the accuracy can be over 90%. Why? Because 9 other numbers exist in our dataset. So if you say the number is not 6, you will be right 9/10 times.
This shows it’s important to choose your evaluation metrics carefully. Accuracy is not a good choice if you want to evaluate your classification tasks. You should choose precision or recall.
What are those? They come up in the False Positive Paradox, so continue reading.
False Positive Paradox
Image by Author
Now, the false positive paradox is a statistical phenomenon that can occur when we test for the presence of a rare event or condition.
It is also known as the “base rate fallacy” or “base rate neglect”.
This paradox means there are more false positive results than positive results when testing rare events.
Let’s look at the example from Data Science.
Fraud Detection

Image by Author
Imagine you are working on an ML model to detect fraudulent credit card transactions. The dataset you are working with includes a large number of normal (non-fraudulent) transactions and a small number of fraudulent transactions. Yet when you deploy your model in the real world, you find that it produces a large number of false positives.
After further investigation, you realize that the prevalence of fraudulent transactions in the real world is much lower than in the training dataset.
Let’s say 1/10,000 transactions will be fraudulent, and suppose the test also has a 5% rate of false positives.
TP = 1 out of 10,000
FP = 10,000*(100-40)/100*0,05 = 499,95 out of 9,999
So when a fraudulent transaction is found, what is the possibility that it really is a fraudulent transaction?
P = 1/500,95 =0,001996
The result is nearly 0.2%. It means when the event gets flagged as fraudulent, there is only a 0.2% probability that it really is a fraudulent event.
And that is a false positive paradox.
Here is how to implement it in Python code.
import pandas as pd
import numpy as np
# Number of normal transactions
normal_count = 9999
# Number of fraudulent transactions
true_positive = 1
# Number of normal transactions flagged as fraudulent by the model
false_positives = 499.95
# Number of fraudulent transactions flagged as normal by the model
false_negatives = 0
# Calculate precision
precision = (true_positive) / true_positive + false_positives
print(f"Precision: {precision:.2f}")
# Calculate recall
recall = (fraud_count) / fraud_count + false_negatives
print(f"Recall: {recall:.2f}")
# Calculate accuracy
accuracy = (
normal_count - false_positives + fraud_count - false_negatives
) / (normal_count + fraud_count)
print(f"Accuracy: {accuracy:.2f}")
You can see that the recall is really high, yet the precision is very low.
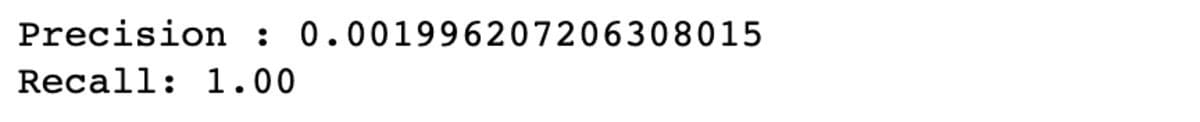
To understand why systems do that, let me explain the precision/recall and precision/recall tradeoff.
Recall (true positive rate) is also called sensitivity. You should first find the positives and find the rate of true positives among them.
Recall = TP / TP + FP
Precision is the accuracy of positive prediction.
Precision = TP / TP + FN
Let’s say you want a classifier that will do sentiment analysis and predict whether the comments will be positive or negative. You might want a classifier that has high recall (it correctly identifies a high percentage of positive or negative comments). However, to have a higher recall, you should be okay with having a lower precision (misclassification of positive comments) because it is more important to delete negative comments than delete a few positive comments occasionally.
On the other hand, if you want to build a spam classifier, you might want a classifier that has high precision. It correctly identifies high percentages of spam, yet once in a while, it allows spam because it is more important to keep important mail.
Now in our case, to find a fraudulent transaction, you sacrifice getting many errors that are not fraudulent, yet if you do so, you have to take precautions, too, like in banking systems. When they detect fraudulent transactions, they begin to do further investigations to be absolutely sure.
Typically they send a message to your phone or email for further approval when doing a transaction over a preset limit, etc.
If you allow your model to have a False negative, then your recall will be law. Yet, if you allow your model to have a False positive, your Precision will be low.
As a data scientist, you should adjust your model or add a step to make further investigations because there might be a lot of False Positives.
Gambler’s Fallacy

Image by Author
Gambler’s fallacy, also known as the Monte Carlo fallacy, is the mistaken belief that if an event happens more frequently than its normal probability, it will happen more often in the following trials.
Let’s look at the example from the Data Science field.
Customer Churn

Image by Author
Imagine that you are building a machine learning model to predict whether the customer will churn based on their past behavior.
Now, you collected many different types of data, including the number of customers interacting with the services, the length of time they have been a customer, the number of complaints they have made, and more.
At this point, you can be tempted to think a customer who has been with the service for a long time is less likely to churn because they have shown a commitment to the service in the past.
However, this is an example of a gambler’s fallacy because the probability of a customer churning is not influenced by the length of time they have been a customer.
The probability of churn is determined by a wide range of factors, including the quality of the service, the customer's satisfaction with the service, and more of these factors.
So if you build a machine learning model, be careful explicitly not to create a column that includes the length of a customer and try to explain the model by using that. At this point, you should realize that this might ruin your model due to Gambler’s fallacy.
Now, this was a conceptual example. Let’s try to explain this by giving an example of the coin toss.
Let’s first look at the changes in the coin toss probability. You might be tempted to think that if the coin has come up heads several times, the possibility in the future will diminish. This is actually a great example of the gambler’s fallacy.
As you can see, in the beginning, the possibility fluctuated. Yet when the number of flips increases, the possibility of getting heads will converge to 0.5.
import random
import matplotlib.pyplot as plt
# Set up the plot
plt.xlabel("Flip Number")
plt.ylabel("Probability of Heads")
# Initialize variables
num_flips = 1000
num_heads = 0
probabilities = []
# Simulate the coin flips
for i in range(num_flips):
if (
random.random() > 0.5
): # random() generates a random float between 0 and 1
num_heads += 1
probability = num_heads / (i + 1) # Calculate the probability of heads
probabilities.append(probability) # Record the probability
# Plot the results
plt.plot(probabilities)
plt.show()
Now, let’s see the output.
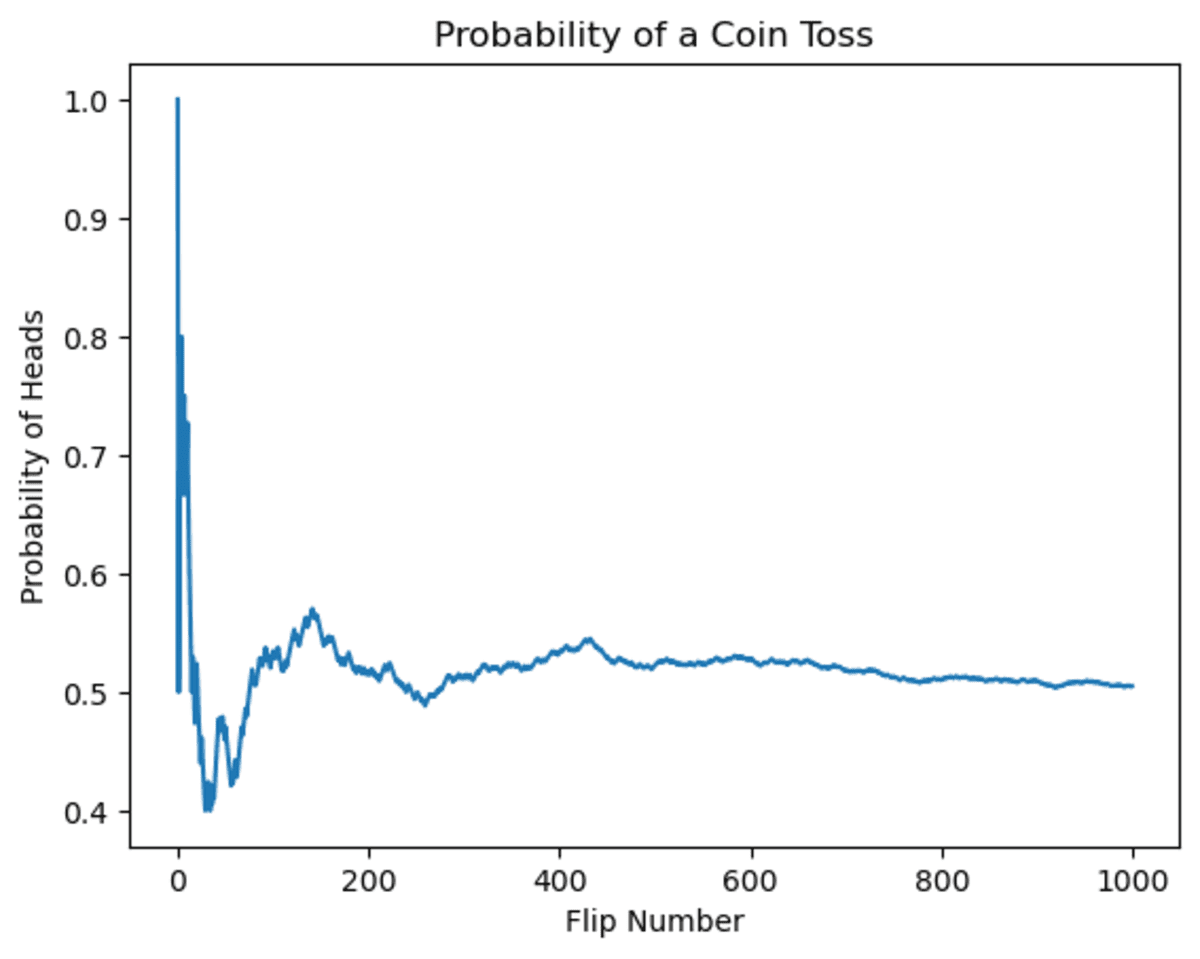
Image by Author
It is obvious that probability fluctuates over time, but as a result, it will converge toward 0.5.
This example shows Gambler’s fallacy because the results of previous flips do not influence the probability of getting heads on any given flip. The probability remains fixed at 50% regardless of what has happened in the past.
Simpsons Paradox

Image by Roland Steinmann from Pixabay
This paradox happens when the relationship between two variables appears to change when data is aggregated.
Now, to explain this paradox, let’s use the built-in data set in seaborn, tips.
Tips

Image by Author
To explain Simpson’s paradox, we will calculate the mean of the average tips women and men made during lunch and overall by using the tips data set. The tips dataset contains data on tips given by customers at a restaurant, like total tips, sex, day, time, and more.
The tips dataset is a collection of data on tips given by customers at a restaurant. It includes information such as the tip amount, the gender of the customer, the day of the week, and the time of day. The dataset can be used to analyze customers' tipping behavior and identify trends in the data.
import seaborn as sns
# Load the tips dataset
tips = sns.load_dataset("tips")
# Calculate the tip percentage for men and women at lunch
men_lunch_tip_pct = (
tips[(tips["sex"] == "Male") & (tips["time"] == "Lunch")]["tip"].mean()
/ tips[(tips["sex"] == "Male") & (tips["time"] == "Lunch")][
"total_bill"
].mean()
)
women_lunch_tip_pct = (
tips[(tips["sex"] == "Female") & (tips["time"] == "Lunch")]["tip"].mean()
/ tips[(tips["sex"] == "Female") & (tips["time"] == "Lunch")][
"total_bill"
].mean()
)
# Calculate the overall tip percentage for men and women
men_tip_pct = (
tips[tips["sex"] == "Male"]["tip"].mean()
/ tips[tips["sex"] == "Male"]["total_bill"].mean()
)
women_tip_pct = (
tips[tips["sex"] == "Female"]["tip"].mean()
/ tips[tips["sex"] == "Female"]["total_bill"].mean()
)
# Create a data frame with the average tip percentages
data = {
"Lunch": [men_lunch_tip_pct, women_lunch_tip_pct],
"Overall": [men_tip_pct, women_tip_pct],
}
index = ["Men", "Women"]
df = pd.DataFrame(data, index=index)
df
Alright, here is our data frame.
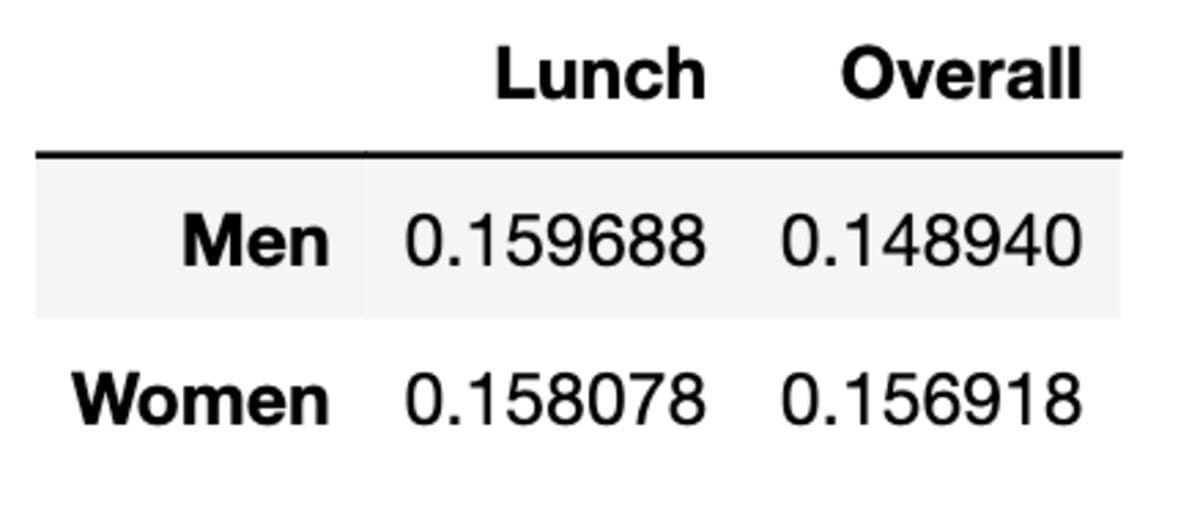
As we can see, the average tip is bigger when it comes to lunch between men and women. Yet when data is aggregated, the mean is changed.
Let’s see the bar chart to see the changes.
import matplotlib.pyplot as plt
# Set the group labels
labels = ["Lunch", "Overall"]
# Set the bar heights
men_heights = [men_lunch_tip_pct, men_tip_pct]
women_heights = [women_lunch_tip_pct, women_tip_pct]
# Create a figure with two subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
# Create the bar plot
ax1.bar(labels, men_heights, width=0.5, label="Men")
ax1.bar(labels, women_heights, width=0.3, label="Women")
ax1.set_title("Average Tip Percentage by Gender (Bar Plot)")
ax1.set_xlabel("Group")
ax1.set_ylabel("Average Tip Percentage")
ax1.legend()
# Create the line plot
ax2.plot(labels, men_heights, label="Men")
ax2.plot(labels, women_heights, label="Women")
ax2.set_title("Average Tip Percentage by Gender (Line Plot)")
ax2.set_xlabel("Group")
ax2.set_ylabel("Average Tip Percentage")
ax2.legend()
# Show the plot
plt.show()
Here is the output.
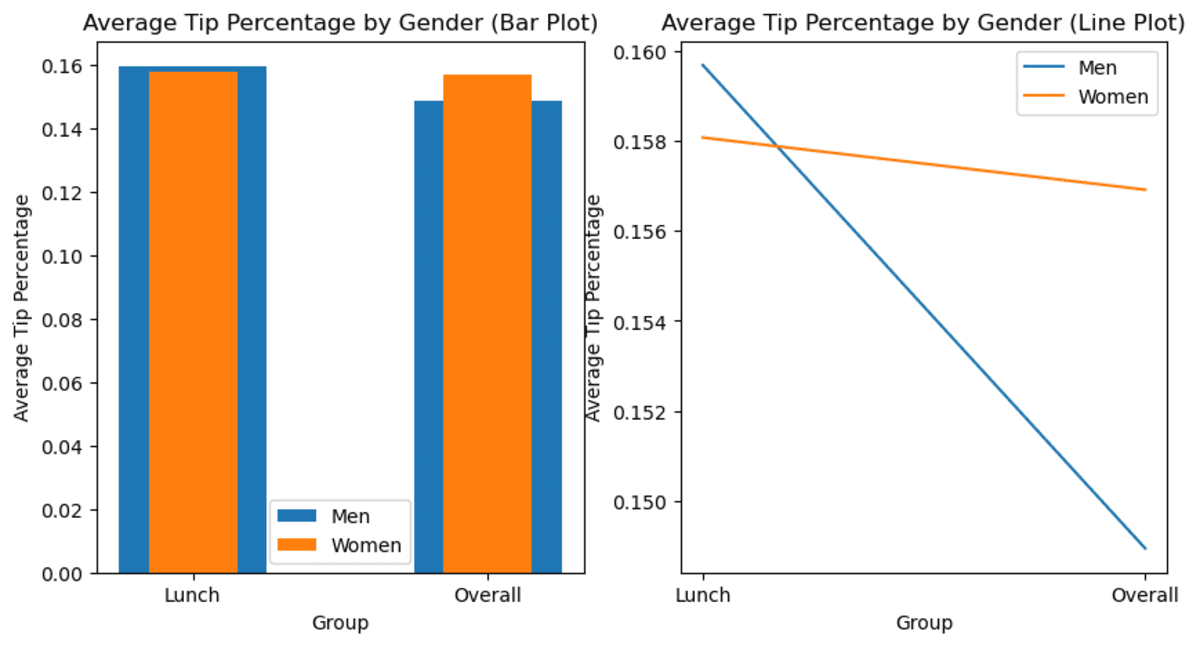
Image by Author
Now, as you can see, the average changes as data are aggregated. Suddenly, you have data showing that overall, women tip more than men.
What is the catch?
When observing the trend from the subset version and extracting meaning from them, be careful not to forget to check whether this trend is still the case for the whole data set or not. Because as you can see, there might not be the case in special circumstances. This can lead a Data Scientist to make a misjudgment, leading to a poor (business) decision.
Berkson’s Paradox
Berkson’s Paradox is a statistical paradox that happens when two variables correlated to each other in data, yet when the data will subsetted, or grouped, this correlation is not observed & changed.
In simple terms, Berkson's Paradox is when a correlation appears to be different in different subgroups of the data.
Now let’s look into it by analyzing the Iris dataset.
Iris Data set

Image by Author
The Iris dataset is a commonly used dataset in machine learning and statistics. It contains data for different observations of irises, including their petal and sepal length and width and the flower species observed.
Here, we will draw two graphs showing the relationship between sepal length and width. But in the second graph, we filter the species as a setosa.
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import linregress
# Load the iris data set
df = sns.load_dataset("iris")
# Subset the data to only include setosa species
df_s = df[df["species"] == "setosa"]
# Create a figure with two subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
# Plot the relationship between sepal length and width.
slope, intercept, r_value, p_value, std_err = linregress(
df["sepal_length"], df["sepal_width"]
)
ax1.scatter(df["sepal_length"], df["sepal_width"])
ax1.plot(
df["sepal_length"],
intercept + slope * df["sepal_length"],
"r",
label="fitted line",
)
ax1.set_xlabel("Sepal Length")
ax1.set_ylabel("Sepal Width")
ax1.set_title("Sepal Length and Width")
ax1.legend([f"R^2 = {r_value:.3f}"])
# Plot the relationship between setosa sepal length and width for setosa.
slope, intercept, r_value, p_value, std_err = linregress(
df_s["sepal_length"], df_s["sepal_width"]
)
ax2.scatter(df_s["sepal_length"], df_s["sepal_width"])
ax2.plot(
df_s["sepal_length"],
intercept + slope * df_s["sepal_length"],
"r",
label="fitted line",
)
ax2.set_xlabel("Setosa Sepal Length")
ax2.set_ylabel("Setosa Sepal Width")
ax2.set_title("Setosa Sepal Length and Width ")
ax2.legend([f"R^2 = {r_value:.3f}"])
# Show the plot
plt.show()
You can see the changes between sepal length and within the setosa species. Actually, it shows a different correlation than other species.
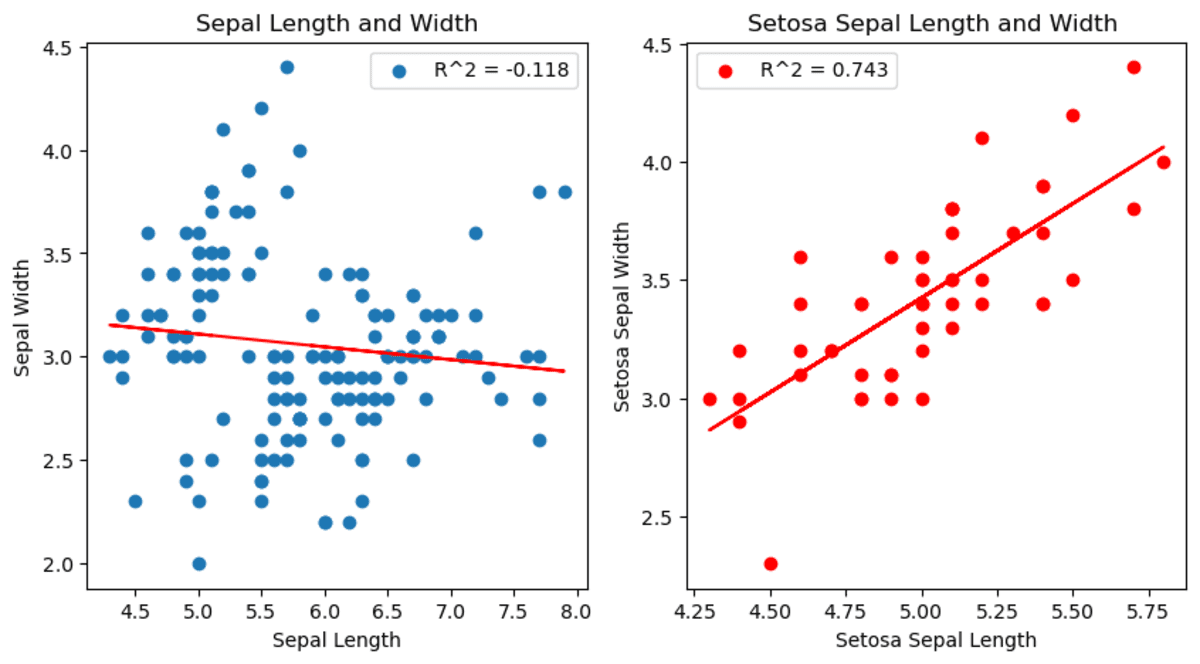
Image by Author
Also, you can see that setosa’s different correlation in the first graph.
In the second graph, you can see that the correlation between sepal width and sepal length has changed. When analyzing all data set, it shows that when sepal length increases, sepal width decreases. However, if we start analyzing by selecting setosa species, the correlation is now positive and shows that when sepal width increases, sepal length increases as well.
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import linregress
# Load the tips data set
df = sns.load_dataset("iris")
# Subset the data to only include setosa species
df_s = df[df["species"] == "setosa"]
# Create a figure with two subplots
fig, ax1 = plt.subplots(figsize=(5, 5))
# Plot the relationship between sepal length and width.
slope, intercept, r_value_1, p_value, std_err = linregress(
df["sepal_length"], df["sepal_width"]
)
ax1.scatter(df["sepal_length"], df["sepal_width"], color="blue")
ax1.plot(
df["sepal_length"],
intercept + slope * df["sepal_length"],
"b",
label="fitted line",
)
# Plot the relationship between setosa sepal length and width for setosa.
slope, intercept, r_value_2, p_value, std_err = linregress(
df_s["sepal_length"], df_s["sepal_width"]
)
ax1.scatter(df_s["sepal_length"], df_s["sepal_width"], color="red")
ax1.plot(
df_s["sepal_length"],
intercept + slope * df_s["sepal_length"],
"r",
label="fitted line",
)
ax1.set_xlabel("Sepal Length")
ax1.set_ylabel("Sepal Width")
ax1.set_title("Sepal Length and Width")
ax1.legend([f"R = {r_value_1:.3f}"])
Here is the graph.
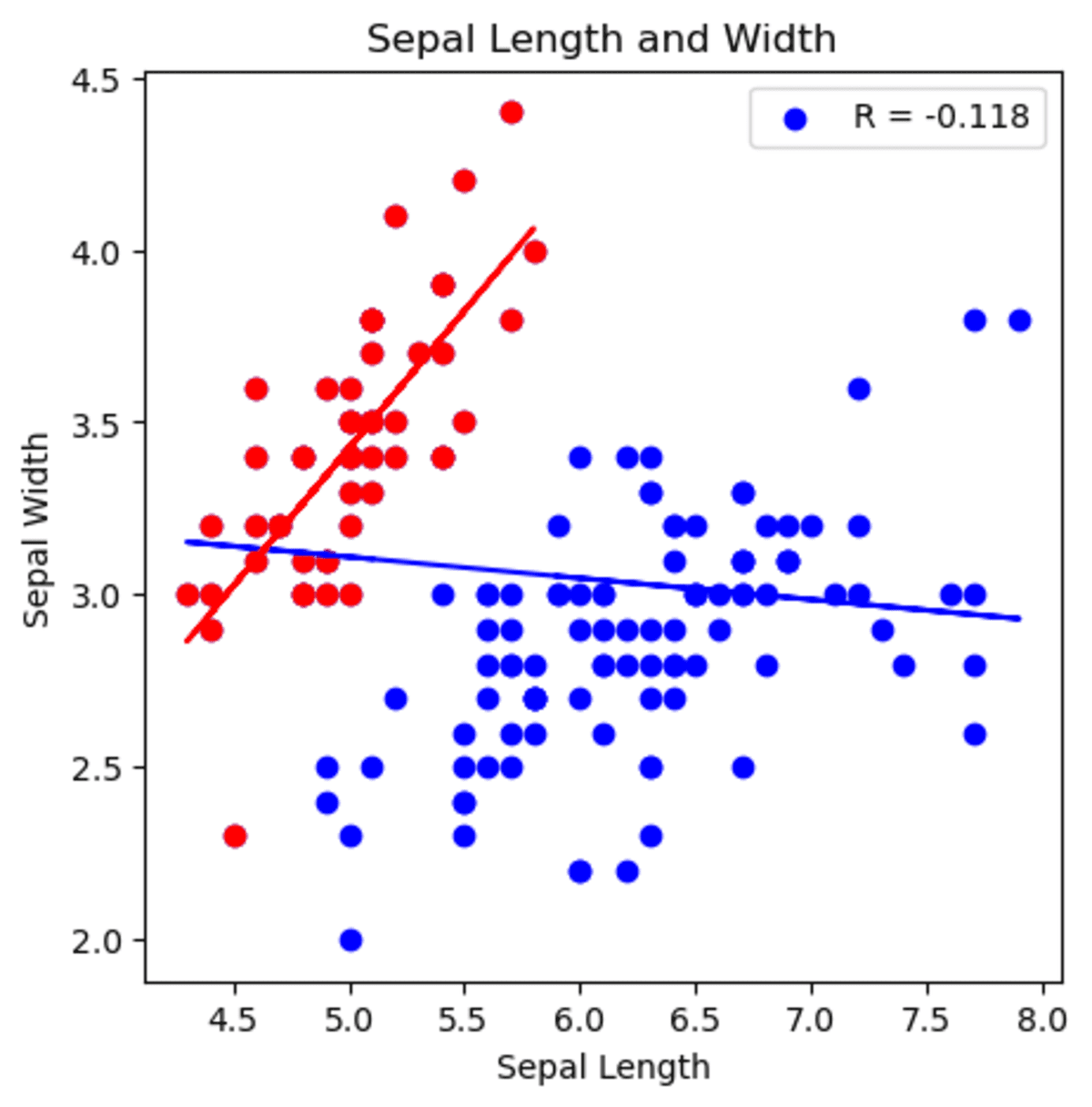
Image by Author
You can see that starting by analyzing with setosa and generalizing the sepal width and length correlation will lead you to make a false statement according to your analysis.
Conclusion
In this article, we examined five statistical paradoxes that data scientists should be aware of in order to do accurate analysis. Let’s suppose you think that you found a trend in your data set, which indicates that when sepal length increases, sepal width increases as well. Yet when looking at the whole data set, it is actually the total opposite.
Or you might be assessing your classification models by looking at the accuracy. You see that even the model that does nothing can achieve over 90% accuracy. If you tried to evaluate your model with accuracy and do analysis accordingly, think about how many miscalculations you can make.
By understanding these paradoxes, we can take steps to avoid common pitfalls and improve the reliability of our statistical analysis. It’s also good to approach data analysis with a healthy dose of skepticism and avoid potential paradoxes and limitations in your analyses.
In conclusion, these paradoxes are important for Data Scientists when it comes to high-level analysis, as being aware of them can improve the accuracy and reliability of our analysis. We also recommend this “Statistics Cheat Sheet” that can help you understand the important terms and equations for statistics and probability and can help you for your next data science interview.
Thanks for reading!
Nate Rosidi is a data scientist and in product strategy. He's also an adjunct professor teaching analytics, and is the founder of StrataScratch, a platform helping data scientists prepare for their interviews with real interview questions from top companies. Connect with him on Twitter: StrataScratch or LinkedIn.
