Bayesian vs Frequentist Statistics in Data Science
Is your statistical alignment Bayesian or a Frequentist?
Image by Author
Before we get into the differences between Bayesian and frequentist statistics, let’s start with their definitions.
What is the Bayesian Approach?
When using statistical inference, you are making judgments about the parameters of a population using data.
Bayesian inference takes into consideration prior knowledge, and the parameter is taken as a random variable. Meaning there is a probability that the event will occur. For example, if we were to flip a coin, Bayesian inference will state that there is no wrong or right answer, and the probability of the coin landing on heads or tails is down to their perspective.
The Bayesian perspective is based on Bayes’ Theorem, a formula that takes into account the probability of an event based on prior knowledge. The formula is shown below, where:
- P(A): the probability of A occurring
- P(B): the probability of B occurring
- P(A|B): the probability of A given event B
- P(B|A): the probability of B given event A
- Pr(A|B): the posterior, the probability of the parameters given the data.
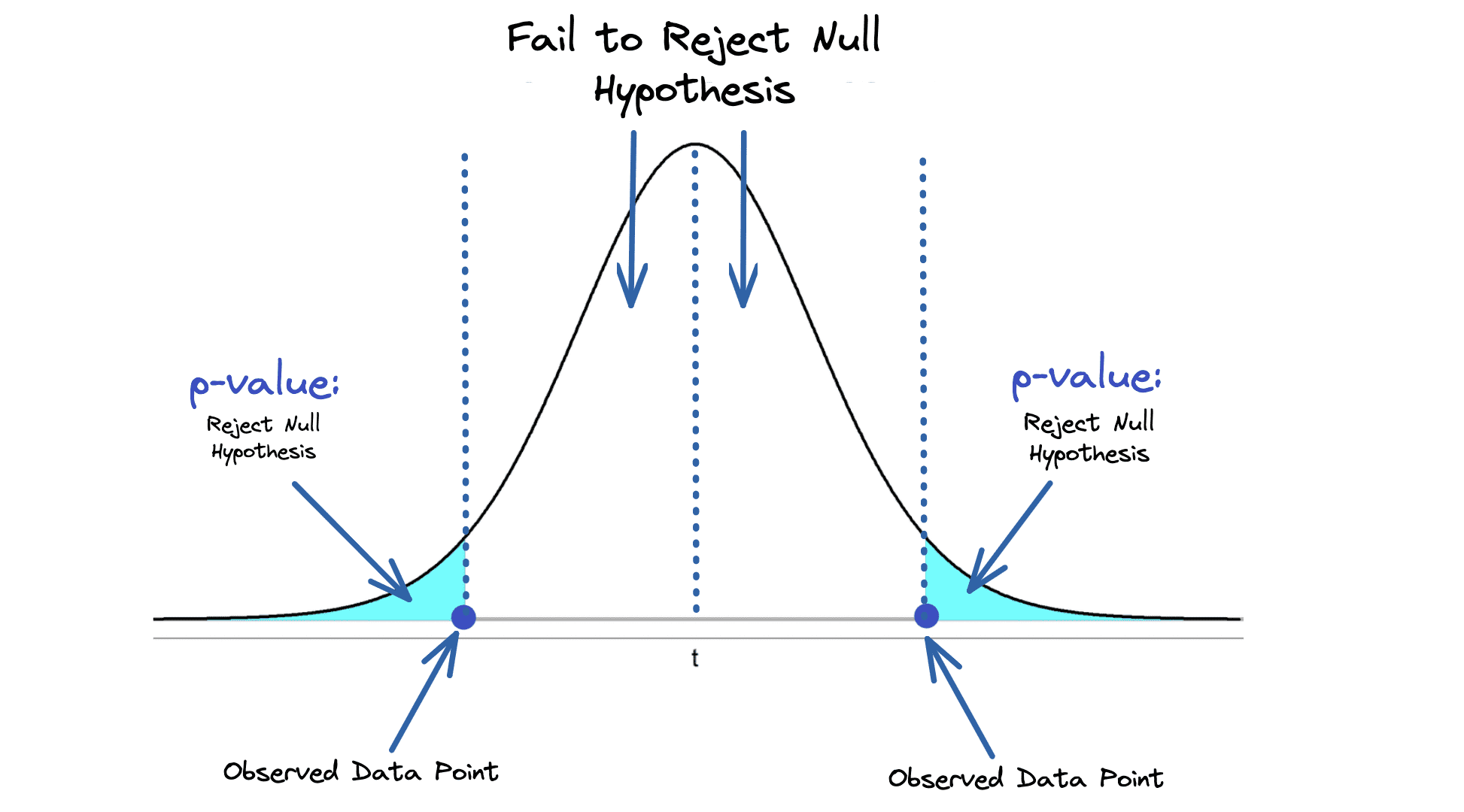
Image by Wikipedia
People that have a Bayesian mindset, view and use probabilities to measure the likelihood of an event happening. It is what they believe. The probability of a hypothesis is calculated and deemed true using prior opinions and knowledge as new data is readily available. This is called prior probability, which is concluded before the project starts.
This prior probability is then converted into a posterior probability, the belief once the project has started.
Prior + Likelihood = Posterior
What is the Frequentist Approach?
Frequentist inference is different. It assumes that events are based on frequencies, and the parameter is not a random variable- meaning there is no probability. Using the same example as above, if you were to flip a coin - frequentist inference will state that there is a correct answer based on frequency. If you were to toss a coin and get tails half of the time, then the probability of getting tails is 50%.
There is a stopping criterion put in place. The stopping rule determines the sample space, therefore knowledge about it is essential for frequentist inference. For example, with the coin toss a frequentist approach may repeat the test 2000 times, or until it's landed on 300 tails. Researchers don’t typically repeat tests this amount of time.
People that have a Frequentist mindset, view and treat probability the same as frequencies. Their probability depends on something happening if it were to be infinitely repeated.
From a frequentist's point of view, the parameters you use to estimate your population are assumed to be fixed. There’s a single true parameter that you will estimate and is not modeled as a probability distribution. When new data is available, you will use it to perform statistical tests and make probabilities about the data.
The most popular computation in frequentist statistics is the p-value, a statistical measurement used to validate your hypotheses. It describes how likely you are to have found a particular set of observations if the null hypothesis (no statistical relationship) is correct.
The shaded blue area in the image below shows the p-value, the probability of an observed result occurring by chance.
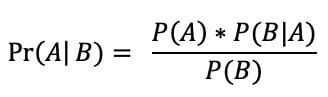
Image by Author
How Does it Apply to Data Science?
Statistics is a huge part of Data Science, and if you’re part of that world - you have come across Bayes’ Theorem, p-value, and other statistical tests. It benefits you as a Data Scientist or someone who works with data to have a good understanding of statistical analysis and the tools out there. There may be a time that you will require them.
Within your team, as you are discussing projects and your next steps - you will start to see who has a Bayesian mindset and who has a Frequentist mindset. Data Scientists will work on probabilistic forecasting which combines residual variance with estimated uncertainty. This is specifically a Bayesian framework. However, it doesn’t rule out some experts wanting to use a frequentist approach.
Depending on the approach you take reflects on the statistical methods you choose. A lot of the fundamentals of data science are built on Bayesian statistics, and some even view frequentist approaches to be a subset of Bayesian theory.
However, when it comes to data science, your focus is on the problem at hand. Many data scientists choose their models based on the problem they are trying to solve. The upper hand that Bayesian approaches have is that in the world of data science, having specific knowledge about the problem is always an advantage.
Bayesian methods are known to be faster, interpretable, user-centered, and have a more intuitive approach to analysis.
I will go into these further below and the differences between the two.
Faster Learning
A Bayesian approach starts with an initial belief, which is backed by gathering evidence. This results in faster learning as you have evidence to support your statement.
A Frequentist approach bases their opinions on facts obtained from the data. Although they have had a look at the data, there has not been any analysis performed to ensure this is evidence. There are no calculations of the probability to back the hypothesis.
Interpretable
Bayesian methods have a variety of flexible models, allowing them to be applied to complex statistical problems. This allows for Bayesian methods to be more easily interpretable.
Frequentist methods are unfortunately not that flexible and typically fail.
User-centered
The two methods have different approaches. The Bayesian method allows for different studies and questions to be included in the project conversation. There is a focus on probable effect sizes.
Whereas, frequentist methods limitate this possibility as it focuses on uncertain significance.
Bayesian vs. Frequentist Summary
| Attributes: | Bayesian: | Frequentist: |
| What is it? | Probability distribution around the parameters | Parameters are fixed and a single point |
| What does it question? | Given the data, what is the probability of the hypothesis? | Is the hypothesis true or false? |
| What does it require? | Prior knowledge/information and any dataset. | A stopping criterion |
| What does it output? | A for or against probability about the hypothesis. | point estimate (p-value) |
| Main advantage | Backed up with evidence and can apply new information | They are simple and easy to use, and does not need prior knowledge |
| Main disadvantage | Requires advanced statistics | Highly dependent on the sample size, and only give a yes or no output |
| When should I use it? | Limited your data when you have priors
Uses more computing power |
With a large amount of data |
Conclusion
I hope this blog has given you a better understanding of the difference between Bayesian approaches and Frequentist approaches. There has been a lot of going back and forth between the two, and if one even exists without the other. My advice is to stick to what makes you feel comfortable and how your brain breaks things down through your personal logic.
If you want a deeper dive, where you can apply your skills and knowledge, I would recommend: Statistics Crash Course for Beginners: Theory and Applications of Frequentist and Bayesian Statistics Using Python
Nisha Arya is a Data Scientist, Freelance Technical Writer and Community Manager at KDnuggets. She is particularly interested in providing Data Science career advice or tutorials and theory based knowledge around Data Science. She also wishes to explore the different ways Artificial Intelligence is/can benefit the longevity of human life. A keen learner, seeking to broaden her tech knowledge and writing skills, whilst helping guide others.
