Elevate Math Efficiency: Navigating Numpy Array Operations
Uncover the art of optimizing math for data analysis and how NumPy transforms complex calculations into simple, efficient spells, making math a breeze.

Image by Author
In this article, we will discover the potency of one of the famous and helpful Python libraries for data analysis, NumPy, where the primary data structure to store the elements and perform operations is a multidimensional array. We will see how this dynamic library makes the complex mathematical task efficient regarding space and time complexity. Also, see how data manipulation and transformation can be made easier regarding effortless operations.
What is Numpy?
Numpy, Scipy, and Matplotlib are Python libraries used in Data Science projects, which provide MATLAB-like functionality.

Image from Wikipedia
Mainly, Numpy has the following Features:
- Typed multidimensional arrays (matrices)
- Fast numerical computations (matrix math)
- High-level math functions
Numpy stands for Numerical Python, the fundamental package required for high-performance computing and data analysis. NumPy is necessary for numerical computations in Python because it is designed for efficiency on large data arrays.
Different Ways to Create Numpy Arrays
Before starting to do operations on numpy arrays, our first aim is to become proficient in creating a numpy array based on our requirements according to the problem statement.
There are multiple ways to create numpy arrays. Some standard and practical methods are mentioned below:
Case-1: Using the np.ones method to create an array of ones:
If we have to create an array of only “ones,” you can utilize this method.
np.ones((3,5), dtype=np.float32)
#Output
[[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]
Case-2: Using the np.zeros method to create an array of zeros:
If we have to create an array of only “zeroes,” you can utilize this method.
np.zeros((6,2), dtype=np.int8)
# Output
[[0 0]
[0 0]
[0 0]
[0 0]
[0 0]
[0 0]]
Case-3: Using the np.arange method:
You can utilize this method if you have to create an array of elements following a sequence.
np.arange(1334,1338)
#Output
[1334 1335 1336 1337]
Case-4: Using the np.concatenate method:
This method is proper when your required array combines one or more arrays.
A = np.ones((2,3))
B = np.zeros((4,3))
C = np.concatenate([A, B])
#Output
[[1. 1. 1.]
[1. 1. 1.]
[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
Case-5: Using the np.random.random method:
It is useful when creating an array with random values.
np.random.random((2,3))
#Output
[[0.30512345 0.10055724 0.89505387]
[0.36219316 0.593805 0.7643694 ]]
Numpy Arrays Operations
Let’s discuss the basic properties of a numpy array with an example:
Code:
a = numpy.array([[1,2,3],[4,5,6]],dtype=numpy.float32)
# Array dimensions, shape, and data types
print (a.ndim, a.shape, a.dtype)
Output:
2 (2, 3) float32
Based on the above code, we have the following points to remember as a conclusion:
- Arrays can have any dimension as a positive integer, including zero (corresponds to a scalar value).
- Arrays are typed and can have data types such as np.uint8, np.int64, np.float32, np.float64
- Arrays are dense. Each element of the array exists and has the same type.
Code:
# Arrays reshaping
a = numpy.array([1,2,3,4,5,6])
a = a.reshape(3,2)
#Output:
[[1 2]
[3 4]
[5 6]]
a = a.reshape(2,-1)
#Output:
[[1 2 3]
[4 5 6]]
a = a.ravel()
#Output:
[1 2 3 4 5 6]
Important points to remember:
- The total number of elements in the array cannot change after the reshaping operation.
- To infer the axis shape, use -1.
- By default, it stores the element in Row-major format, while on the other hand, in MATLAB, it is column-major.
Numpy Arrays Broadcasting
Broadcasting allows performing operations on arrays of different shapes as long as they are compatible. Smaller dimensions of an array are virtually expanded to match the dimensions of the larger array.
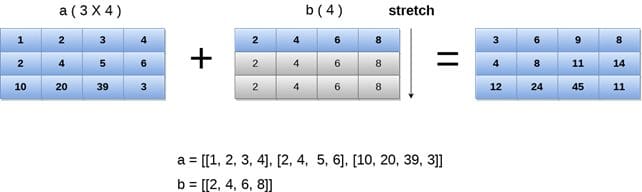
Image from Javatpoint
Code:
# arrays broadcasting
a = numpy.array([[1, 2], [3, 4], [5, 6]])
b = numpy.array([10, 20])
c = a + b # Broadcasting the 'b' array to match the dimensions of 'a'
The example involves a 2D NumPy array 'a' with dimensions (3, 2) and a 1D array 'b' with shape (2). Broadcasting allows the operation 'a + b' to virtually expand 'b' to match 'a' in the second dimension, resulting in element-wise addition between 'a' and the expanded 'b'.
Arrays Indexing and Slicing
- Slices are views. Writing to a slice overwrites the original array.
- A list or boolean array can also index it.
- Python indexing Syntax:
start_index : stop_index: step_size
Code:
a = list(range(10))
# first 3 elements
a[:3] # indices 0, 1, 2
# last 3 elements
a[-3:] # indices 7, 8, 9
# indices 3, 5, 7
a[3:8:2]
# indices 4, 3, 2 (this one is tricky)
a[4:1:-1]
As you know, an image can also be visualized as a multidimensional array. So, slicing can also be helpful to perform some mathematical operations on images. Some of the important and advanced examples are mentioned below to increase your understanding:
# Select all but one-pixel border
pixel_matrix[1:-1,1:-1]
# swap channel order
pixel_matrix = pixel_matrix[:,:,::-1]
# Set dark pixels to black
pixel_matrix[pixel_matrix<10] = 0
# select 2nd and 4th-row
pixel_matrix[[1,3], :]
Arrays Aggregation and Reduction
Now, we will start with aggregation operations on numpy arrays. Generally, the operations that you can perform are as follows:
- Finding the sum and product of all the elements of the array.
- Finding the maximum and minimum element in the array
- Find the count of a particular element in an array
- We can also find other parameters using the linear algebra module, including Matrix Determinant, Matrix Trace, Matrix Eigenvalues and eigenvectors, etc.
Let’s start discussing each functionality with examples:
Case-1: Algebraic sum of all the elements present in the array
array_1 = numpy.array([[1,2,3], [4,5,6]])
print(array_1.sum())
#Output:
21
Case-2: Maximum element in the array
array_1 = numpy.array([[1,2,3], [4,5,6]])
print(array_1.max())
#Output:
6
Case-3: Minimum element in the array
array_1 = numpy.array([[1,2,3], [4,5,6]])
print(array_1.min())
#Output:
1
Case-4: Position/Index of the element in the array where the maximum element is in place
array_1 = numpy.array([[1,2,3], [4,5,6]])
print(array_1.argmax())
#Output:
5
Case-5: Position/Index of the element in the array where the minimum element is in place
array_1 = numpy.array([[1,2,3], [4,5,6]])
print(array_1.argmin())
#Output:
0
While finding the position, you can observe that it considers any multidimensional array into a 1-D array and then compute it.
Case-6: Mean/Average of all the elements in an array
array_1 = numpy.array([[1,2,3], [4,5,6]])
print(array_1.mean())
#Output:
3.5
Case-7: Dot product/Scalar product of two multidimensional arrays
array_1 = numpy.array([[1,2], [4,5]])
array_2 = numpy.array([[1,-1,2], [3,7,-2]])
t = array_1.dot(array_2)
print(t)
#Output:
[[ 7 13 -2]
[19 31 -2]]
Vectorization in Numpy Arrays
Vectorization enables performing operations on entire arrays instead of looping through individual elements. It leverages optimized low-level routines, leading to faster and more concise code.
Code:
a = numpy.array([1, 2, 3, 4, 5])
b = numpy.array([10, 20, 30, 40, 50])
c = a + b # Element-wise addition without explicit loops
Based on the above example, you can see that two NumPy arrays, named 'a' and 'b', are created. While performing the operation 'a + b', where we are performing element-wise addition between the arrays using the vectorization concept, resulting in a new array 'c' containing the sum of corresponding elements from 'a' and 'b'. So, because of the element-wise operation, the program avoids running explicit loops and utilizes optimized routines for efficient computation.
Array Concatenation
Case-1: Suppose you have two or more arrays to concatenate using the concatenate function, where you have to join the tuple of the arrays.
Code:
# concatenate 2 or more arrays using concatenate function row-wise
numpy_array_1 = numpy.array([1,2,3])
numpy_array_2 = numpy.array([4,5,6])
numpy_array_3 = numpy.array([7,8,9])
array_concatenate = numpy.concatenate((numpy_array_1, numpy_array_2, numpy_array_3))
print(array_concatenate)
#Output:
[1 2 3 4 5 6 7 8 9]
Case 2: Suppose you have an array with more than one dimension; then, to concatenate the arrays, you must mention the axis along which those have to be concatenated. Otherwise, it will be performed along the first dimension.
Code:
# concatenate 2 or more arrays using concatenate function column-wise
array_1 = numpy.array([[1,2,3], [4,5,6]])
array_2 = numpy.array([[7,8,9], [10, 11, 12]])
array_concatenate = numpy.concatenate((array_1, array_2), axis=1)
print(array_concatenate)
#Output:
[[ 1 2 3 7 8 9]
[ 4 5 6 10 11 12]]
Maths Functions and Universal Functions
These universal functions are also known as ufuncs. Element-wise operations are performed in these functions. For Examples:
- np.exp
- np.sqrt
- np.sin
- np.cos
- np.isnan
Code:
A = np.array([1,4,9,16,25])
B = np.sqrt(A)
#Output
[1. 2. 3. 4. 5.]
Performance Comparisons
While performing numerical computations, Python requires much time if we have big calculations. If we take a matrix of shape 1000 x 1000 matrix and do the matrix multiplication, then the time required by Python and numpy are:
- Python triple loop takes > 10 min
- Numpy takes ~0.03 seconds
So, from the above example, we can see that numpy requires significantly less time than standard python, so our latency reduces in real-life projects related to Data Science, which has massive data to process.
Wrapping it Up
In this article, we discussed the numpy arrays. So, to conclude our session, let’s summarize the advantages of numpy over Python:
- Numpy has array-oriented computing.
- Numpy efficiently implemented multidimensional arrays.
- Numpy is mainly designed for scientific computing.
- Numpy contains standard mathematical functions for faster computation on arrays without loops.
- Numpy has inbuilt Linear algebra and random number generation modules to work with and Fourier transform capabilities.
- Numpy also contains tools for reading and writing arrays to disk and working with memory-mapped files.
Aryan Garg is a B.Tech. Electrical Engineering student, currently in the final year of his undergrad. His interest lies in the field of Web Development and Machine Learning. He have pursued this interest and am eager to work more in these directions.
