Must-Know: What is the curse of dimensionality?

Editor's note: This post was originally included as an answer to a question posed in our 17 More Must-Know Data Science Interview Questions and Answers series earlier this year. The answer was thorough enough that it was deemed to deserve its own dedicated post.

"As the number of features or dimensions grows, the amount of data we need to generalize accurately grows exponentially."

- Charles Isbell, Professor and Senior Associate Dean, School of Interactive Computing, Georgia Tech

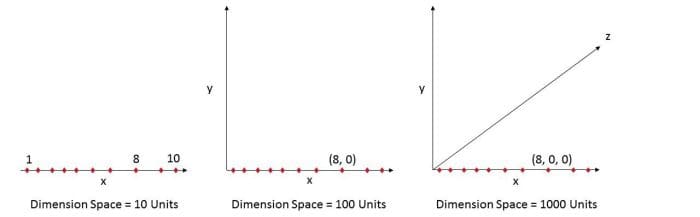
Let’s take an example below. Fig. 1 (a) shows 10 data points in one dimension i.e. there is only one feature in the data set. It can be easily represented on a line with only 10 values, x=1, 2, 3... 10.

But if we add one more feature, same data will be represented in 2 dimensions (Fig.1 (b)) causing increase in dimension space to 10*10 =100. And again if we add 3rd feature, dimension space will increase to 10*10*10 = 1000. As dimensions grows, dimensions space increases exponentially.

   10^1 = 10

   10^2 = 100

   10^3 = 1000 and so on...

This exponential growth in data causes high sparsity in the data set and unnecessarily increases storage space and processing time for the particular modelling algorithm. Think of image recognition problem of high resolution images 1280 × 720 = 921,600 pixels i.e. 921600 dimensions. OMG. And that’s why it’s called Curse of Dimensionality. Value added by additional dimension is much smaller compared to overhead it adds to the algorithm.

Bottom line is, the data that can be represented using 10 space units of one true dimension, needs 1000 space units after adding 2 more dimensions just because we observed these dimensions during the experiment. The true dimension means the dimension which accurately generalize the data and observed dimensions means whatever other dimensions we consider in dataset which may or may not contribute to accurately generalize the data.

Related:

• Must-Know: How to evaluate a binary classifier
• Must-Know: Why it may be better to have fewer predictors in Machine Learning models?
• 17 More Must-Know Data Science Interview Questions and Answers