Using Data Mining to Predict the Winter Olympics Medal Counts in Sochi

By Dan Graettinger with Tim Graettinger

• Which nation will bring home the most medals at the upcoming Winter Olympics in Sochi, Russia?

• Will any nation from Africa, South America, or the Middle East finally break through and win a medal?

• Why do some nations win a bundle of medals while others win only a few?

• Can data mining give us the answers to these questions?


This last question came into my mind four years ago after the Winter Games in Vancouver. As a data miner working with Discovery Corps, Inc., I use data about the past to predict the future all the time. We help businesses decide which potential customers are the most likely to want their product or service. We help non-profit organizations predict which small-dollar donors have the potential to become big-dollar donors. If an organization has data on the past, we can help them predict the future. So I knew that data mining techniques could give us an estimate of the number of medals each nation might win; but I wondered how close we could get to the actual outcomes.

It was a tantalizing project. My mind immediately began to analyze the problem. What is it about a nation that causes it to win medals at the Olympics – and would I be able to find data on those characteristics? Wealth had to play a part. A nation whose people are struggling to survive is not going to have many individuals with the leisure time for recreational pursuits like becoming world class in a sporting event. Also, geography might be part of the equation. I was going way out on a limb here, but I didn't think a nation like Western Sahara would probably bring home a lot of medals at the WINTER Olympics! The other thought that immediately struck me was that, in order to win a medal at a sport like downhill skiing, a nation has to have mountains. Clearly, I was going to need to start collecting data – as much as I could – about the nations of the world. (That is, after I got my boss's okay to pursue this project when we had some down time.)

What Kind of Data?

As data miners know, the data you expect to tell you the story isn't always the stuff that actually does the job , so I decided to cast my net as wide as I could, gathering as many different pieces of data as possible. I wanted all kinds of data on the nations of the world, even data that I didn't expect to be relevant to the outcome (See Appendix B for the list of data I eventually used.) And in fact, a column of data that I thought would be irrelevant and might easily have deleted turned out to be the single most useful variable in predicting the number of medals a nation would win! Fortunately, I was able to find data in many categories:

• Economic
• Population
• Human Development
• Geography
• Religion
• Politics and Freedom

Thankfully, there were some good sources out there , and I collected enough data that I felt I had a good chance to predict some meaningful outcomes. But would it be enough? There is more than one way to go about predicting the medal count at the Olympics, and the route before me was the "30,000 feet" approach. Far from having information on individual athletes in the various events, I would be working entirely from data about nations.

Excellence in anything has a lot to do with individual motivation. Instead, I would be approaching the problem from perhaps the most aggregate viewpoint possible. Then again, what might I learn about nations while studying their ability to produce excellence? Yes, I could probably make better predictions if I had the resources of a news organization, gathering experts on every sport, predicting the winners in each, and summing them up into national totals. But that wouldn't tell me anything about the great questions – the 'Why?' questions. Why is a nation able to produce excellent individuals? What factors contribute to such success? If I found answers to these questions, perhaps those answers might cross over from athletic excellence to other areas of human endeavor: science and technology, the arts, theology, etc. Well … that was getting way beyond the original scope of the project. For the time being, I would just focus on predicting the nations' medal counts in Sochi.

Building the Models

Once I had married the data on the nations to their medal counts in the last two Winter Games, my team at Discovery Corps and I could begin exploring it and preparing to build a predictive model. We decided that we would first use a logistic regression to predict which nations would win at least one medal and which would come home empty-handed . As we got the results from profiling each variable against our outcome (medals > 0), immediately the most useful variable of the bunch showed itself – and it was a real shock! I had dreamed up this project after watching the Winter Olympics, but I knew I'd have to wait four years for my chance to predict the outcome at the next Winter Games. So we decided in the interim to predict the medal counts at the London Summer Games of 2012 .

When we picked up the data again this year to make our Winter predictions, my subconscious data miner's habit of not deleting data kept me from removing the column of medal counts from the summer games. To our shock, the medal count from the preceding summer games was the best variable for predicting a nation's medal count in the winter games! At the last two Winter Games, no nation won a medal without having won at least one medal in the preceding Summer Olympics. I never expected that! Our predictive model would ultimately fill in a zero for the anticipated medal count in Sochi if the nation did not win a medal in London. Also during the profiling stage, we saw other variables rise to the top: migration rate, doctors per thousand people, latitude of the capital city, value of the nation's exports, and some measures of gross domestic product. Ultimately, once we built our logistic model, it had a 96.5% correct rating. Not too shabby! (Correct predictions included those instances where we predicted the nation would win a medal and it did as well as instances where we predicted a nation would not win a medal and it didn’t. All others outcomes were ‘misses’.)

Since our goal was to predict how many medals each country would win, we needed to go beyond the binary outcome the logistic regression used (simply whether the nation would win a medal or not). So we decided to create a linear regression model that would predict actual medal counts. And for readers who are interested in the nitty gritty details, we also had to scale the results of our linear regression to the correct number of medals being awarded this year. (Every four years the number of events changes, as some new events are added to the program and occasionally some are removed. Thus the total number of medals ebbs and flows.) So we put together the linear regression, scaled it, and got our results!

The Survey Says …

The table below shows our predictions.

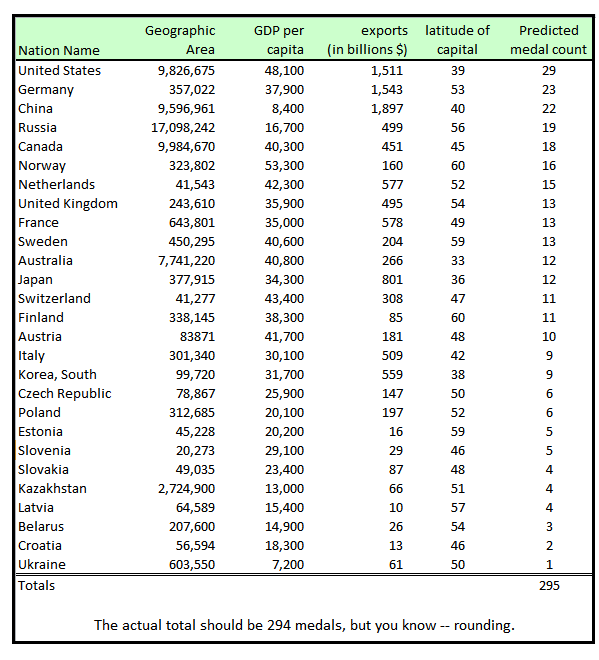
(For all nations not shown, we are predicting a medal count of zero.)
The four variables the linear model uses to make these predictions are as follows:

• Geographic area - We are a little perplexed to find this variable in the model. Our best guess is that it may reflect the nation's population and/or the genetic diversity in the population and/or the presence of mountain ranges on which to ski and snowboard. Also, it does separate the relatively larger nations of the world from the many small (geographically and population-wise) island nations in the Caribbean and the Pacific.

• GDP per capita - This was no surprise. It seems to confirm my hunch that nations whose people are affluent can afford to spend time pursuing excellence in sports, while poorer nations cannot.

• Value of Exports – A measure of a nation’s total economic power that seems to complement per capita GDP.

• Latitude of Nation's Capital - No surprise here. The further your country is from the equator, the more snow and ice you'll have – and the more medals you'll win at sports contested on snow and ice!

So as we look at the table, we see nations far from the equator, with modern economies, with relatively high wealth, and which are relatively large geographically. Some other interesting facts pop out. Of the 27 nations listed, only seven are outside of Europe. China, Japan, South Korea, and Kazakhstan represent Asia, while the United States and Canada are in North America. The only other nation – and the only one located in the southern hemisphere! – is Australia. It will be interesting to see how close the prediction for the U.S. will be. In 2010, the U.S. team set a new record with 37 total medals, only their second time winning the total medal count.

For full details, please visit http://www.discoverycorpsinc.com/winter-olympic-medal-predict_1/