Dark Knowledge Distilled from Neural Network
Geoff Hinton never stopped generating new ideas. This post is a review of his research on “dark knowledge”. What’s that supposed to mean?
For almost any machine learning algorithm, a very simple way to improve its performance is to train many different models on the same data and then to average their predictions. But it requires too much computation at test time.
Geoffrey Hinton et al. claimed that when extracting knowledge from data, we do not need to worry about the test computation. It seems not hard to distill most of the knowledge into a smaller model for deployment, which they called “dark knowledge”. A little creepy name, but not in a harmful way.
Their paper on dark knowledge includes two main parts.
- Model compression: transfer the language learned from the ensemble models into a single smaller model to reduce test computation.
- Specialist Networks: training models specialized on a confusable subset of the classes to reduce the time to train an ensemble.
Let’s compress the cumbersome models.
The principal idea is that once the cumbersome model has been trained, we can use a different kind of training called ‘distillation’ to transfer the knowledge to a single smaller model. The same idea has been introduced by Caruana in 2006 while he used a different way of transferring the knowledge, which Hinton shows is a special case of distillation.
To put it in another way, for each data point, we have a predicted distribution using the bigger ensemble network. We will train the smaller network using the output distribution as “soft targets” instead of the true labels. In this way, we can train the small model to generalize in the same way as the large model.
Before training the small model, Hinton increases the entropy of the posteriors and get a much softer distribution by using a transform that “raises the temperature”. A higher temperature will produce a softer probability distribution over classes.
The result on MNIST is surprisingly good, even when they tried omitting some digit. When they omitted all examples of the digit 3 during the transfer training, the distilled net gets 98.6% of the test 3s correct even though 3 is a mythical digit it has never seen.
Train Specialist to Disambiguate
Another question is that sometimes the computation required at training time is also excessive, so how can we make an ensemble mine knowledge more efficiently. Hinton’s answer is to encourage each “specialist” to focus on resolving different confusions.
The specialist estimates two things: whether the image is in my special subset and what the relative probabilities of the classes in the special subset are. For example, in ImageNet, we can make one “specialist” to see examples in mushrooms while another focuses on sports cars.
More technical details can be found on their paper and slides, which has this example – see slides for details.
Experiment on MNIST
Vanilla backprop in a 784 -> 800 -> 800 -> 10 net with rectified linear hidden units gives 146 test errors.
Training a 784 -> 1200 -> 1200 -> 10 net using dropout and weight constraints and jittering the input, eventually gets 67 errors.
It turns out, that much of this improvement can be transferred to a much smaller neural net. Using both the soft targets obtained from the big net and the hard targets, you get 74 errors in the 784 -> 800 -> 800 -> 10 net.
The transfer training uses the same training set but with no dropout and no jitter
It is just vanilla backprop (with added soft targets).
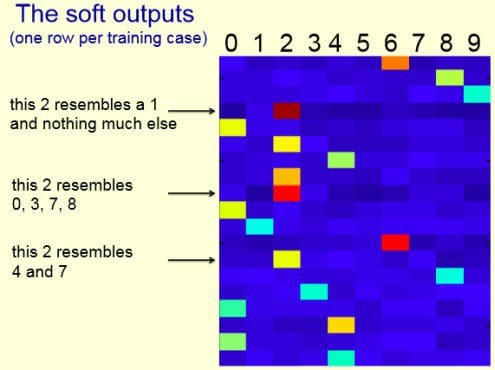
The soft targets contain almost all the knowledge.
The big net learns a similarity metric for the training digits even though this isn’t the objective function for learning.