How to Tackle a Lottery with Mathematics
With mathematical rigor and narrative flair, Adam Kucharski reveals the tangled history of betting and science. The house can seem unbeatable. In this book, Kucharski shows us just why it isn't. Even better, he shows us how the search for the perfect bet has been crucial for the scientific pursuit of a better world.
By Adam Kucharski.
This post is based on excerpt from 
The Perfect Bet: How Science and Math Are Taking the Luck Out of Gambling, by Adam Kucharski.
With mathematical rigor and narrative flair, Adam Kucharski reveals the tangled history of betting and science. The house can seem unbeatable, but Kucharski shows us just why it isn't. Even better, he shows us how the search for the perfect bet has been crucial for the scientific pursuit of a better world.
Whenever a big lottery rollover arrives, interest in math spikes. From January’s billion-dollar US Powerball jackpot to the record prize in the UK Lotto, people want to know what their chances are, and how they can be improved. At first glance, such calculations might seem like a matter of straightforward probability. But as we delve further into lottery strategy, the questions involved become more interesting—and far trickier.
From a mathematical point of view, the most popular way to answer the “should I buy a lottery ticket?” question is to calculate its expected value—the average payoff if you played the game an infinite number of times. All you need to do is work out the probability of each outcome,and multiply it by the money you’d end up with if that outcome occurred.
For example,if a lottery has a jackpot of $10m, and you have a 1 in 4 million chance of winning, the expected value of a ticket is $2.50. If that ticket costs $2 to buy, you’d end up profiting in the long run. In most lotteries, there’s also a chance you could pick up lower-tier prizes too – which can push the expect value even higher.
But would you really play such a lottery? Although you’d come out on top eventually, you might have to burn through a lot of money first. Mathematical theory can handle infinite timescales; wallets cannot.
To avoid bankruptcy arriving before profits, successful bettors—whether at the blackjack table or the races—often employ bankroll management techniques. One of the best known is the “Kelly criterion”. Devised by physicist John Kelly in the 1950s, this aims to maximize the long-term growth of your money, balancing potential profits with risk of loss. For a given bet, the Kelly criterion tells players to wager the following fraction of their total wealth:
In the lottery example above, the expected net profit is $0.50 ($2.50 minus the $2 cost of the ticket). And the net profit if successful is $10m. So according to the Kelly criterion, the optimal investment is to bet a fraction 1/20,000,000 of your total wealth.
As the minimum possible investment is a $2 ticket, this suggests a single lottery ticket isn’t a worthwhile investment unless you already have a $40m bankroll.

Figure 1: How many tickets should a billionaire buy? Plot shows number of tickets that should be purchased according to the Kelly criterion, if you had a $1bn bankroll. Results given for US Powerball, and lotteries in which you have to match 6 numbers from 49 or 59 balls, assuming a $2 ticket price.
What about the rest?
So far we’ve just considered a single ticket and single jackpot: the calculations ignore other prize tiers, and other tickets you may have bought. This can be a particularly important omission if lotteries have “roll-down” weeks. This happens when the prize money reaches a certain set limit, and gets re-distributed to the lower prize tiers. How should you pick your tickets to ensure you maximise your chances of picking up a certain prize?
Let’s say you want to match 2 numbers, which is typically the lowest prize tier in a lottery. What’s the minimum number of tickets you should buy to achieve this? Combinatorialists call such a set of tickets a “lotto design”, and they are not always easy to find. In 1998, Zoltán Füredi and colleagues proved that for the Hungarian lottery—in which players have to choose 5 numbers from 90—it is necessary buy a minimum of 100 tickets to guarantee you’ll match 2 numbers. For the Canadian 6/49 lottery, where you have to pick 6 numbers from a possible 49, it’s been shown that you need buy a minimum of 19 tickets to get 2 matching numbers.
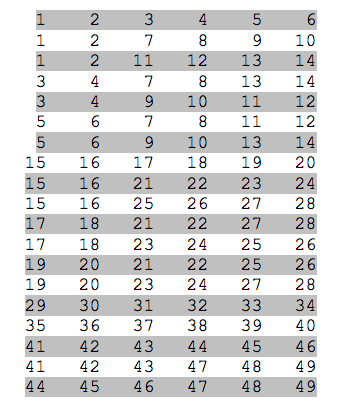
Figure 2: Lotto design guaranteed to match 2 numbers in a 6/49 lottery. Designed by Stefan Vandevelde (http://lottery.merseyworld.com/Wheel/wheel19.html)
In some cases,the best lotto design remains unknown. For a 6/49 lottery, the smallest number of tickets required to guarantee a match of 3 numbers is an open problem. Lottery researcher Peter Rosendahl provided an upper bound for the value, when he found numerically a combination of 163 tickets that worked, but the true minimum number of tickets may be lower than this.
As well as considering multiple tickets, we also need to account for multiple players. When roll-downs appear in a lottery, the expect value of a game increases, but so does the chance of splitting the jackpot with others. One option is to turn to psychology, and try to avoid popular numbers—such as birthdays—that would dilute your winnings if you won.
Alternatively, you could try and influence the outcome of the game by brute force. In the Massachusetts Cash WinFall lottery, which ran from 2005 to 2012, a roll-down would occur if the prize money hit $2m. Syndicates therefore bulk-bought tickets once the jackpot topped $1.7m, as a roll-down would likely appear on the next draw. However, in August 2012, when the jackpot was only at $1.6m, one syndicate bought up so many tickets that it forced a roll-down in the next draw.This caught out the other lottery syndicates, who were still waiting for the prize to hit $1.7m, and as a result the group netted several hundred thousand dollars in profit.

The outcome that week was a big surprise, but perhaps it’s less surprising where the winning syndicate came from. The group were originally from MIT, and their lottery operation had started - naturally - with a college math project.
Bio: Adam Kucharski is a lecturer in mathematical modeling at the London School of Hygiene & Tropical Medicine and an award-winning science writer. He studied at the University of Warwick before completing a PhD in mathematics at the University of Cambridge. The winner of the 2012 Wellcome Trust Science Writing Prize, Kucharski lives in London.
Related:
