Deep Learning Research Review: Reinforcement Learning
This edition of Deep Learning Research Review explains recent research papers in Reinforcement Learning (RL). If you don't have the time to read the top papers yourself, or need an overview of RL in general, this post has you covered.
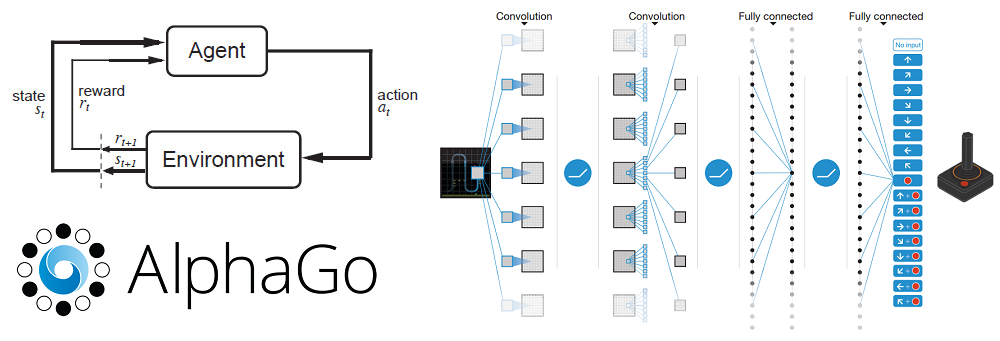
This is the 2nd installment of a new series called Deep Learning Research Review. Every couple weeks or so, I’ll be summarizing and explaining research papers in specific subfields of deep learning. This week focuses on Reinforcement Learning.
Last time was Generative Adversarial Networks ICYMI
Introduction to Reinforcement Learning
3 Categories of Machine Learning
Before getting into the papers, let’s first talk about what reinforcement learning is. The field of machine learning can be separated into 3 main categories.
- Supervised Learning
- Unsupervised Learning
- Reinforcement Learning
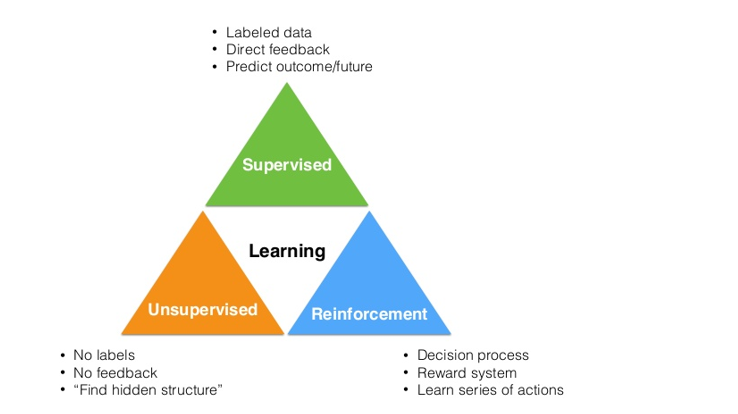
The first category, supervised learning, is the one you may be most familiar with. It relies on the idea of creating a function or model based on a set of training data, which contains inputs and their corresponding labels. Convolutional Neural Networks are a great example of this, as the images are the inputs and the outputs are the classifications of the images (dog, cat, etc).
Unsupervised learning seeks to find some sort of structure within data through methods of cluster analysis. One of the most well-known ML clustering algorithms, K-Means, is an example of unsupervised learning.
Reinforcement learning is the task of learning what actions to take, given a certain situation/environment, so as to maximize a reward signal. The interesting difference between supervised and reinforcement learning is that this reward signal simply tells you whether the action (or input) that the agent takes is good or bad. It doesn’t tell you anything about what the best action is. Contrast this to CNNs where the corresponding label for each image input is a definite instruction of what the output should be for each input. Another unique component of RL is that an agent’s actions will affect the subsequent data it receives. For example, an agent’s action of moving left instead of right means that the agent will receive different input from the environment at the next time step. Let’s look at an example to start off.
The RL Problem
So, let’s first think about what have in a reinforcement learning problem. Let’s imagine a tiny robot in a small room. We haven’t programmed this robot to move or walk or take any action. It’s just standing there. This robot is our agent.

Like we mentioned before, reinforcement learning is all about trying to understand the optimal way of making decisions/actions so that we maximize some reward R. This reward is a feedback signal that just indicates how well the agent is doing at a given time step. The action A that an agent takes at every time step is a function of both the reward (signal telling the agent how well it’s currently doing) and the state S, which is a description of the environment the agent is in. The mapping from environment states to actions is called our policy P. The policy basically defines the agent’s way of behaving at a certain time, given a certain situation. Now, we also have a value function V which is a measure of how good each position is. This is different from the reward in that the reward signal indicates what is good in the immediate sense, while the value function is more indicative of how good it is to be in this state/position in the long run. Finally, we also have a model M which is the agent’s representation of the environment. This is the agent’s model of how it thinks that the environment is going to behave.

Markov Decision Process
So, let’s now think back to our robot (the agent) in the small room. Our reward function is dependent on what we want the agent to accomplish. Let’s say that we want it to move to one of the corners of the room where it will receive a reward. The robot will get a +25 when it reaches this point, and will get a -1 for every time step it takes to get there. We basically want the robot to get the corner as fast as possible. The actions the agent can take are moving north, south, east, or west. The agent’s policy can be a simple one, where the behavior is that the agent will always move to the location with the higher value function. Makes sense right? A position with a high value function = good to be in this position (with regards to long term reward).
Now, this whole RL environment can be described with a Markov Decision Process. For those that haven’t heard the term before, an MDP is a framework for modeling an agent’s decision making. It contains a finite set of states (and value functions for those states), a finite set of actions, a policy, and a reward function. Our value function can be split into 2 terms.
- State-value function V: The expected return from being in a state S and following a policy π. This return is calculated by looking at summation of the reward at each future time step (The gamma refers to a constant discount factor, which means that the reward at time step 10 is weighted a little less than the reward at time step 1).
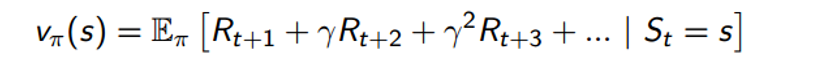
- Action-value function Q: The expected return from being in a state S, following a policy π, and taking an action a (Equation will be same as above except that we have an additional condition that At = a).
Now that we have all the components, what do we do with this MDP? Well, we want to solve it, of course. By solving an MDP, you’ll be able to find the optimal behavior (policy) that maximizes the amount of reward the agent can expect to get from any state in the environment.
Solving the MDP
We can solve an MDP and get the optimum policy through the use of dynamic programming and specifically through the use of policy iteration (there is another technique called value iteration, but won’t go into that right now). The idea is that we take some initial policy π1 and evaluate the state value function for that policy. The way we do this is through the Bellman expectation equation.
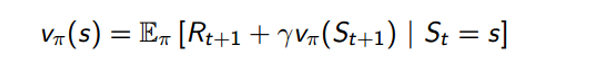
This equation basically says that our value function, given that we’re following policy π, can be decomposed into the expected return sum of the immediate reward Rt+1 and the value function of the successor state St+1. If you think about it closely, this is equivalent to the value function definition we used in the previous section. Using this equation is our policy evaluationcomponent. In order to get a better policy, we use a policy improvement step where we simply act greedily with respect to the value function. In other words, the agent takes the action that maximizes value.
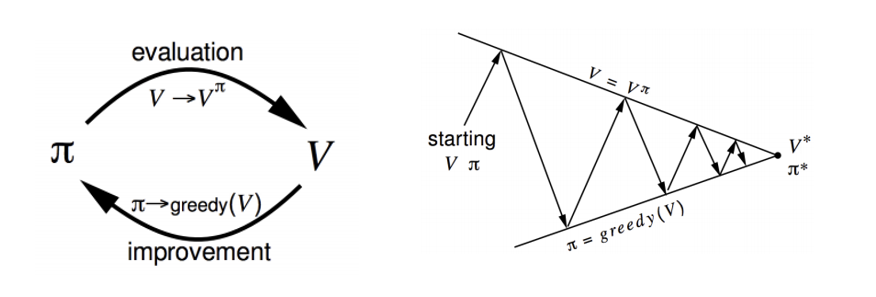
Now, in order to get the optimal policy, we repeat these 2 steps, one after the other, until we converge to optimal policy π*.
When You’re Not Given an MDP
Policy iteration is great and all, but it only works when we have a given MDP. The MDP essentially tells you how the environment works, which realistically is not going to be given in real world scenarios. When not given an MDP, we use model free methods that go directly from the experience/interactions of the agents and the environment to the value functions and policies. We’re going to be doing the same steps of policy evaluation and policy improvement, just without the information given by the MDP.
The way we do this is instead of improving our policy by optimizing over the state value function, we’re going to optimize over the action value function Q. Remember how we decomposed the state value function into the sum of immediate reward and value function of the successor state? Well, we can do the same with our Q function.
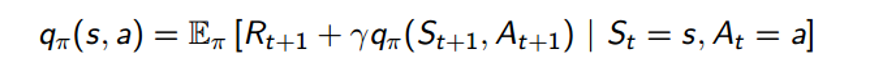
Now, we’re going to go through the same process of policy evaluation and policy improvement, except we replace our state value function V with our action value function Q. Now, I’m going to skip over the details of what changes with the evaluation/improvement steps. To understand MDP free evaluation and improvement methods, topics such as Monte Carlo Learning, Temporal Difference Learning, and SARSA would require whole blogs just themselves (If you are interested, though, please take a listen to David Silver’s Lecture 4 and Lecture 5). Right now, however, I’m going to jump ahead to value function approximation and the methods discussed in the AlphaGo and Atari Papers, and hopefully that should give a taste of modern RL techniques. The main takeaway is that we want to find the optimal policy π* that maximizes our action value function Q.
Value Function Approximation
So, if you think about everything we’ve learned up until this point, we’ve treated our problem in a relatively simplistic way. Look at the above Q equation. We’re taking in a specific state S and action A, and then computing a number that basically tells us what the expected return is. Now let’s imagine that our agent moves 1 millimeter to the right. This means we have a whole new state S’, and now we’re going to have to compute a Q value for that. In real world RL problems, there are millions and millions of states so it’s important that our value functions understand generalization in that we don’t have to store a completely separate value function for every possible state. The solution is to use a Q value function approximation that is able to generalize to unknown states.
So, what we want is some function, let’s call is Qhat, that gives a rough approximation of the Q value given some state S and some action A.
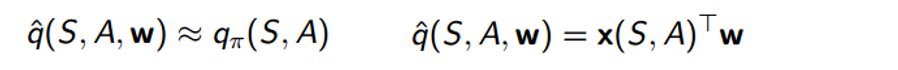
This function is going to take in S, A, and a good old weight vector W (Once you see that W, you already know we’re bringing in some gradient descent ). It is going to compute the dot product between x (which is just a feature vector that represents S and A) and W. The way we’re going to improve this function is by calculating the loss between the true Q value (let’s just assume that it’s given to us for now) and the output of the approximate function.
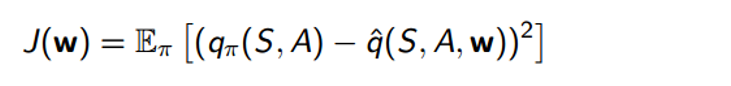
After we compute the loss, we use gradient descent to find the minimum value, at which point we will have our optimal W vector. This idea of function approximation is going to be very key when taking a look at the papers a little later.
Just One More Thing
Before getting to the papers, just wanted to touch on one last thing. An interesting discussion with the topic of reinforcement learning is that of exploration vs exploitation. Exploitation is the agent’s process of taking what it already knows, and then making the actions that it knows will produce the maximum reward. This sounds great, right? The agent will always be making the best action based on its current knowledge. However, there is a key phrase in that statement. Current knowledge. If the agent hasn’t explored enough of the state space, it can’t possibly know whether it is really taking the best possible action. This idea of taking actions with the main purpose of exploring the state space is called exploration.
This idea can be easily related to a real world example. Let’s say you have a choice of what restaurant to eat at tonight. You (acting as the agent) know that you like Mexican food, so in RL terms, going to a Mexican restaurant will be the action that maximizes your reward, or happiness/satisfaction in this case. However, there is also a choice of Italian food, which you’ve never had before. There’s a possibility that it could be better than Mexican food, or could be a lot worse. This tradeoff between whether to exploit an agent’s past knowledge vs trying something new in hope of discovering a greater reward is one of the major challenges in reinforcement learning (and in our daily lives tbh).
Other Resources for Learning RL
Phew. That was a lot of info. By no means, however, was that a comprehensive overview of the field. If you’d like a more in-depth overview of RL, I’d strongly recommend these resources.
- David Silver (from Deepmind) Reinforcement Learning Video Lectures
- My personal notes from the RL course
- Sutton and Barto’s Reinforcement Learning Textbook (This is really the holy grail if you are determined to learn the ins and outs of this subfield)
- Andrej Karpathy’s Blog Post on RL (Start with this one if you want to ease into RL and want to see a really well done practical example)
- UC Berkeley CS 188 Lectures 8-11
- Open AI Gym: When you feel comfortable with RL, try creating your own agents with this reinforcement learning toolkit that Open AI created
