Toward Increased k-means Clustering Efficiency with the Naive Sharding Centroid Initialization Method
What if a simple, deterministic approach which did not rely on randomization could be used for centroid initialization? Naive sharding is such a method, and its time-saving and efficient results, though preliminary, are promising.
The k-means algorithm is a simple yet effective approach to clustering. k points are (usually) randomly chosen as cluster centers, or centroids, and all dataset instances are plotted and added to the closest cluster. After all instances have been added to clusters, the centroids, representing the mean of the instances of each cluster are re-calculated, with these re-calculated centroids becoming the new centers of their respective clusters. Cluster membership is then reset, and the new centroids are used to re-plot and all instances and add them to their closest centroid cluster. This iterative process continues until convergence -- centroid locations remain constant between successive clustering iterations -- is reached.
The k-means Cluster Initialization Problem
One of the greatest challenges in k-means clustering is positioning the initial cluster centers, or centroids, as close to optimal as possible, and doing so in an amount of time deemed reasonable. Traditional k-means utilizes a randomization process for initializing these centroids -- though this is not the only approach -- but poor initialization can lead to increased numbers of required clustering iterations to reach convergence, a greater overall runtime, and a less-efficient algorithm overall.
If you consider that an iteration of the distance calculations required to compare each instance to each centroid takes constant time, then there are 2 aspects of the k-means algorithm that can be, and often are, targeted for optimization:
- Centroid initialization, such that the initial cluster centers are placed as close as possible to the optimal cluster centers
- Selection of the optimal value for k (the number of clusters, and centroids) for a particular dataset
The actual clustering method of the k-means algorithm, which follows centroid initialization, and which is iterated upon until the “best” centroid location is found, is highly sensitive to the initial placement of centroids. The better the initial centroid placement, generally the fewer iterations are required, and the faster and more efficient the algorithm is. Research into improved centroid initialization has yielded both clever methods and improved results, but these methods are often resource intensive and/or time-consuming.
What if the trade-off between computational efficiency and the effectiveness of centroid initialization methods was moot? What if a simple, deterministic approach which did not rely on randomization could be used for centroid initialization? And what if it was computationally simple enough that it relied on very few calculations, dramatically reducing the initialization time, lowering the number of clustering iterations required, and shortening the overall execution time of the k-means algorithm, all while producing comparable accuracy of results?
The Naive Sharding Centroid Initialization Algorithm
Classical k-means clustering utilizes random centroid initialization. In order for randomization to be properly performed, the entire space being occupied by all instances in all dimensions is first to be determined. This means that all instances in the dataset must be enumerated, and a record must be kept of the minimum and maximum values of each attribute, constituting the boundaries of the various planes in n-dimensional space,
The sharding centroid initialization algorithm proceeds in a very simple manner, and is primarily dependent on the calculation of a composite summation value reflecting all of the attribute values of an instance. Once this composite value is computed, it is used to sort the instances of the dataset. The dataset is then horizontally split into k pieces, or shards. Finally, the original attributes of each shard are independently summed, their mean is computed, and the resultant collection of rows of shard attribute mean values becomes the set of centroids to be used for initialization.
Sharding initialization is expected to execute much quicker than random centroid initialization, especially considering that the time needed for randomly initializing centroids for increasingly complex datasets (more instances and more attributes) grows superlinearly, and can be extremely time-consuming given complex enough data; sharding initialization executes in linear time, and is not dependent on data complexity.
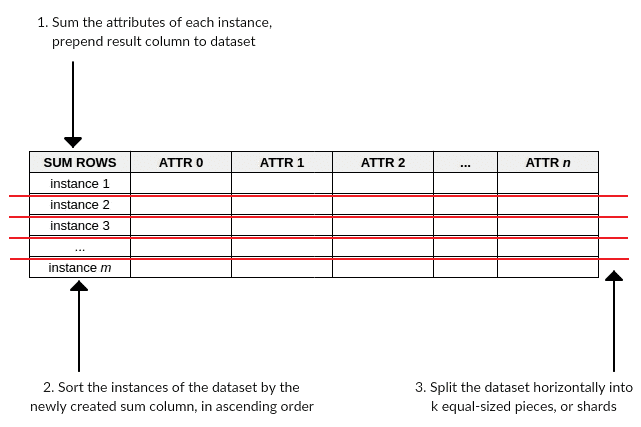
Figure 1: Sorting by composite value and sharding.
An overview of naive sharding is as follows:
- Step 1: Sum the attribute (column) values for each instance (row) of a dataset, and prepend this new column of instance value sums to the dataset
- Step 2: Sort the instances of the dataset by the newly created sum column, in ascending order
- Step 3: Split the dataset horizontally into k equal-sized pieces, or shards
- Step 4: For each shard, sum the attribute columns (excluding the column created in step 1), compute its mean, and place the values into a new row; this new row is effectively one of the centroids used for initialization
- Step 5: Add each centroid row from each shard to a new set of centroid instances
- Step 6: Return this set of centroid instances to the calling function for use in the k-means clustering algorithm
As previously promised, the algorithm is very simple -- almost embarrassingly so.
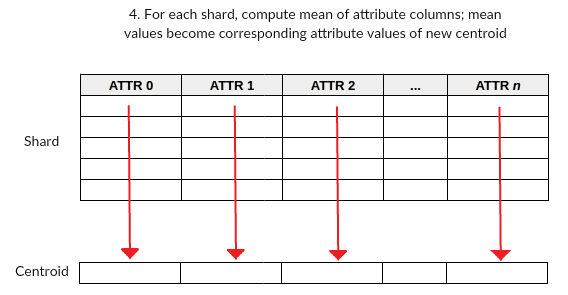
Figure 2: Shard attribute means become centroid attribute values.
Naive Sharding Implementation and Experimentation
First off, the above overview makes no mention of data preprocessing techniques, as they are of separate concern. However, as with clustering in general, outcomes will be affected by data values, and in the case of naive sharding, data scaling will be of particular importance, given that a composite value could be overly-influenced by a single overwhelming value's range otherwise.
These concerns aside, below is a Python implementation of the naive sharding centroid initialization algorithm.
Since Scikit-learn's k-means algorithm implementation allows for the passing of initial centroids, we can demonstrate naive sharding without reinventing the wheel.
Centroids using naive sharding (scaled data) -------------------------------------------- [[ 0.17666667 0.25166667 0.07864407 0.06 ] [ 0.41944444 0.42916667 0.54949153 0.505 ] [ 0.69 0.63666667 0.77457627 0.80833333]]
The initial centroids are plotted (in 2 dimensions) against the scaled Iris dataset below (centroids in yellow):

Figure 3. Initial centroids via naive sharding.
You can see that they are placed central to the action (at least in 2 dimensional space), relative to potential non-optimal random placement: any centroids placed in the empty upper right quadrant would certainly not be optimal, and any recovery through successive iterations of the algorithm would be compounded if multiple centroids ended up close together in such empty space.
Of course, non-optimal centroid placement can be recovered from in k-means (one of its strengths), but what kind of recovery would be required, practically speaking? Let's perform the actual k-means clustering, first with random centroid initialization, and then with naive sharding centroid initialization, and compare results.
Predicted --------- [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 2 2 2 1 2 2 2 2 2 2 1 2 2 2 2 2 1 2 1 2 1 2 2 1 1 2 2 2 2 2 1 1 2 2 2 1 2 2 2 1 2 2 2 1 2 2 1] Actual ------ [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2] Accuracy: 0.886666666667 Iterations: 9 Inertia: 6.99811400483
Predicted --------- [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 2 2 2 1 2 2 2 2 2 2 1 2 2 2 2 2 1 2 1 2 1 2 2 1 1 2 2 2 2 2 1 1 2 2 2 1 2 2 2 1 2 2 2 1 2 2 1] Actual ------ [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2] Accuracy: 0.886666666667 Iterations: 1 Inertia: 6.99811400483
Bearing in mind that the ground truth of this dataset is known, and that we have proceeded accordingly, both centroid initialization methods result in an accuracy of approximately 89%, and share the same inertia, or within-cluster sum-of-squares. The only difference is that naive sharding took 1 iteration of k-means to get to the result, while random initialization took 9.
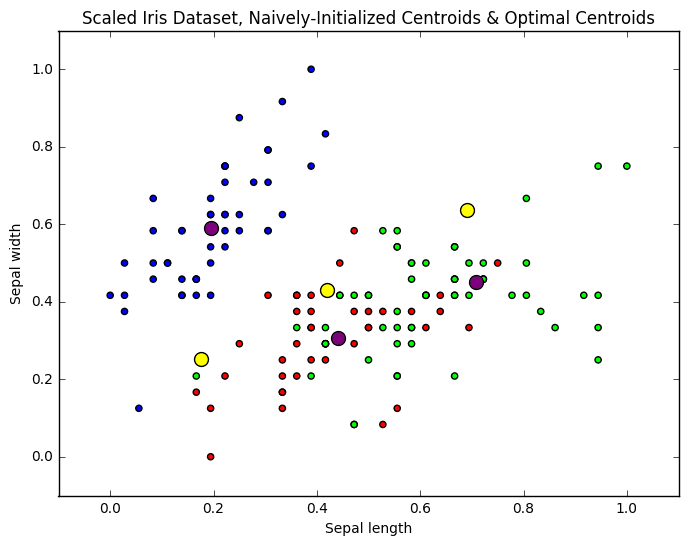
Figure 4. Initial centroids (yellow) via naive sharding vs. optimal centroids (purple) via k-means clustering.
Who cares, though, right? Well, on a toy dataset like Iris -- with its 150 instances -- that iteration difference and the processing time that comes with it, may not be important, but with a much larger dataset the savings in time -- with equivalent of competitive accuracy of results -- could be significant.
For instance, let's investigate a slightly larger dataset, 3D Road Network:
Centroids using naive sharding (scaled data) -------------------------------------------- [[ 0.13546377 0.11747167 0.05458445 0.07378088] [ 0.25125091 0.25433351 0.14654911 0.09003291] [ 0.50881844 0.39242227 0.22776759 0.10992592] [ 0.59676316 0.48547428 0.31513051 0.13666101] [ 0.62017295 0.55034077 0.37331935 0.16647871] [ 0.65406449 0.58429265 0.42799943 0.20076948] [ 0.70674852 0.6121824 0.52515724 0.23930599] [ 0.78915972 0.66302398 0.62559139 0.28339069] [ 0.87849087 0.72028317 0.73596579 0.35175889] [ 0.95252989 0.81382297 0.85959953 0.50055848]]
Running the above experiments on this dataset provides the following insight:
Random initialization --------------------- Iterations: 29 Inertia: 17709.5474904 Elapsed time: 70.814582 Naive sharding initialization ----------------------------- Iterations: 11 Inertia: 17584.089322 Elapsed time: 2.584894
As the ground truth of this dataset is unknown, a nominal value of 10 was used for k.
A few items of note:
- The inertia of the model built from naive sharding centroids was minimally lower than that of the randomly initialized centroid model
- Naive sharding resulted in less than half of the required clustering iterations to reach optimal centroid placement (11 vs. 29)
- Perhaps most importantly, the elapsed time of the random centroid model was approximately 28 times that of the naive centroid model, suggesting that the real time savings of the proposed algorithm is in the placement of the initial centroids, as opposed to the clustering iterations -- though both may be a factor with datasets of significant enough size
Conclusion
There are no exuberant claims being made that this method of centroid initialization should supplant random initialization. Only a few simple experiments have been presented here, but significantly more testing during this research resulted in further support of the naive sharding centroid initialization method. There were definitely dataset/k value combinations during research which resulted in fewer required iterations from random centroid initialization; however, in the majority of such cases the number of iterations was competitive, and often the overall execution time was still better for naive sharding initialization. Surprisingly, in most of these cases the inertia was actually lower for naive sharding as well, suggesting that the deterministic approach may be providing empirically better centroids from a distance perspective.
Centroid initialization, much like real estate, is mostly about location, location, location. The naive centroid initialization method provides an alternative approach to this critical clustering step which may help identify the best starting location for centroids, and do so relatively quickly.
Related:
