 Making Predictive Models Robust: Holdout vs Cross-Validation
Making Predictive Models Robust: Holdout vs Cross-Validation
The validation step helps you find the best parameters for your predictive model and prevent overfitting. We examine pros and cons of two popular validation strategies: the hold-out strategy and k-fold.
By Robert Kelley, Dataiku.
When evaluating machine learning models, the validation step helps you find the best parameters for your model while also preventing it from becoming overfitted. Two of the most popular strategies to perform the validation step are the hold-out strategy and the k-fold strategy.
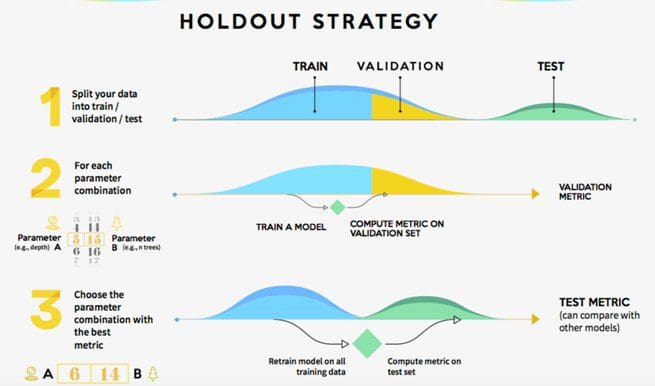
Pros of the hold-out strategy: Fully independent data; only needs to be run once so has lower computational costs.
Cons of the hold-out strategy: Performance evaluation is subject to higher variance given the smaller size of the data.
K-fold validation evaluates the data across the entire training set, but it does so by dividing the training set into K folds – or subsections – (where K is a positive integer) and then training the model K times, each time leaving a different fold out of the training data and using it instead as a validation set. At the end, the performance metric (e.g. accuracy, ROC, etc. — choose the best one for your needs) is averaged across all K tests. Lastly, as before, once the best parameter combination has been found, the model is retrained on the full data.
Pros of the K-fold strategy: Prone to less variation because it uses the entire training set.
Cons of the K-fold strategy: Higher computational costs; the model needs to be trained K times at the validation step (plus one more at the test step).

Bio: Robert Kelley is Product Marketing Manager at Dataiku. As a former business analyst, one of his main focuses is bringing concepts of machine learning and data science to data and business analysts. An amateur baseball statistics analyst in his spare time, Robert holds a B.S. in Economics and Mathematics from Duke University and an MBA from HEC-Paris.
Related:

 Making Predictive Models Robust: Holdout vs Cross-Validation
Making Predictive Models Robust: Holdout vs Cross-Validation