When Bayes, Ockham, and Shannon come together to define machine learning
A beautiful idea, which binds together concepts from statistics, information theory, and philosophy.
Introduction
It is somewhat surprising that among all the high-flying buzzwords of machine learning, we don’t hear much about the one phrase which fuses some of the core concepts of statistical learning, information theory, and natural philosophy into a single three-word-combo.
Moreover, it is not just an obscure and pedantic phrase meant for machine learning (ML) Ph.Ds and theoreticians. It has a precise and easily accessible meaning for anyone interested to explore, and a practical pay-off for the practitioners of ML and data science.
I am talking about Minimum Description Length. And you may be thinking what the heck that is…
Let’s peel the layers off and see how useful it is…
Bayes and his Theorem
We start with (not chronologically) with Reverend Thomas Bayes, who by the way, never published his idea about how to do statistical inference, but was later immortalized by the eponymous theorem.

It was the second half of the 18th century, and there was no branch of mathematical sciences called “Probability Theory”. It was known simply by the rather odd-sounding “Doctrine of Chances” — named after a book byAbraham de Moievre. An article called, “An Essay towards solving a Problem in the Doctrine of Chances”, first formulated by Bayes, but edited and amended by his friend Richard Price, was read to Royal Society and published in the Philosophical Transactions of the Royal Society of London, in 1763. In this essay, Bayes described — in a rather frequentist manner — the simple theorem concerning joint probability which gives rise to the calculation of inverse probability i.e. Bayes Theorem.
Many a battle have been fought since then between the two warring factions of statistical science — Bayesians and Frequntists. But for the purpose of the present article, let us ignore the history for a moment and focus on the simple explanation of the mechanics of the Bayesian inference. For a super intuitive introduction to the topic, please see this great tutorial by Brandon Rohrer. I will just concentrate on the equation.
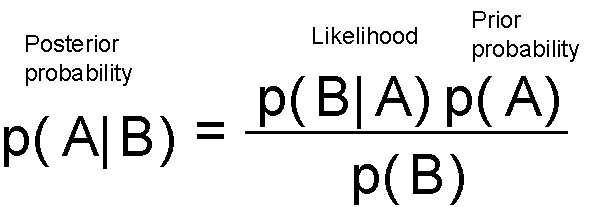
This essentially tells that you update your belief (prior probability) after seeing the data/evidence (likelihood) and assign the updated degree of belief to the term posterior probability. You can start with a belief, but each data point will either strengthen or weaken that belief and you update your hypothesis all the time.
Sounds simple and intuitive? Great.
I did a trick in the last sentence of the paragraph though. Did you notice? I slipped in a word “Hypothesis”. That is not normal English. That is formal stuff :-)
In the world of statistical inference, a hypothesis is a belief. It is a belief about about the true nature of the process (which we can never observe), that is behind the generation of a random variable (which we can observe or measure, albeit not without noise). In statistics, it is generally defined as a probability distribution. But in the context of machine learning, it can be thought of any set of rules (or logic or process), which we believe, can give rise to the examples or training data, we are given to learn the hidden nature of this mysterious process.
So, let us try to recast the Bayes’ theorem in different symbols — symbols pertaining to data science. Let us denote, data by D and hypothesis by h. This means we apply Bayes’ formula to try to determine what hypothesis the data came from, given the data. We rewrite the theorem as,
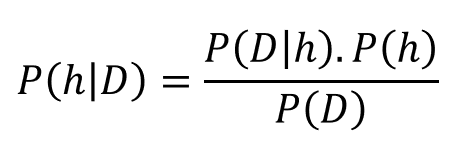
Now, in general, we have a large (often infinite) hypothesis space i.e. many hypotheses to choose from. The essence of Bayesian inference is that we want to examine the data to maximize the probability of one hypothesis which is most likely to give rise to the observed data. We basically want to determine argmax of the P(h|D) i.e. we want to know for which h, observed D is most probable. To that end, we can safely drop the term in the denominator P(D) because it does not depend on the hypothesis. This scheme is known by rather tongue twisting name of maximum a posteriori (MAP).
Now, we apply following mathematical tricks,
- The fact that maximization works similarly for logarithm as for the original function i.e. taking logarithm does not change the maximization problem.
- Logarithm of product is the sum of individual logarithms
- Maximization of a quantity is equivalent to minimization of the negative quantity
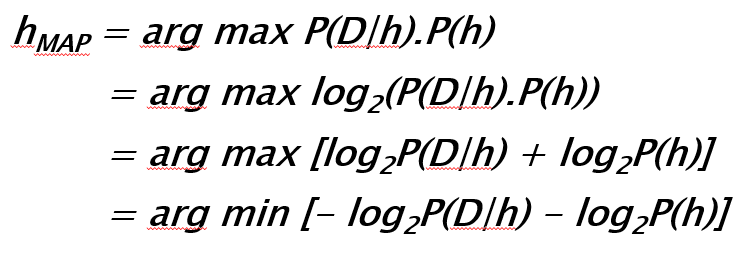
Curiouser and curiouser…those terms with negative logarithm of 2 look familiar… from Information Theory!
Enters Claude Shannon.
Shannon
It will take many a volume to describe the genius and strange life of Claude Shannon, who almost single handedly laid the foundation of information theory and ushered us into the age of modern high-speed communication and information exchange.
Shannon’s M.I.T. master’s thesis in electrical engineering has been called the most important MS thesis of the 20th century: in it the 22-year-old Shannon showed how the logical algebra of 19th-century mathematician George Boole could be implemented using electronic circuits of relays and switches. This most fundamental feature of digital computers’ design — the representation of “true” and “false” and “0” and “1” as open or closed switches, and the use of electronic logic gates to make decisions and to carry out arithmetic — can be traced back to the insights in Shannon’s thesis.
But this was not his greatest achievement yet.
In 1941, Shannon went to Bell Labs, where he worked on war matters, including cryptography. He was also working on an original theory behind information and communications. In 1948, this work emerged in a widely celebrated paper published in Bell Lab’s research journal.
Shannon defined the quantity of information produced by a source — for example, the quantity in a message — by a formula similar to the equation that defines thermodynamic entropy in physics. In its most basic terms, Shannon’s informational entropy is the number of binary digits required to encode a message. And for a message or event with probability p, the most efficient (i.e. compact) encoding of that message will require -log2(p) bits.
And that is precisely the nature of those terms appearing in the maximum a posteriori expression derived from the Bayes’ theorem!
Therefore, we can say that in the world of Bayesian inference, most probable hypothesis depends on two terms which evoke the sense of length — rather minimum length.

But what could be the notion of the length in those terms?
Length (h): Occam’s Razor
William of Ockham (circa 1287–1347) was an English Franciscan friar and theologian, and an influential medieval philosopher. His popular fame as a great logician rests chiefly on the maxim attributed to him and known as Occam’s razor. The term razor refers to distinguishing between two hypotheses either by “shaving away” unnecessary assumptions or cutting apart two similar conclusions.
The precise words attributed to him are: entia non sunt multiplicanda praeter necessitatem (entities must not be multiplied beyond necessity). In statistical parlance, that means we must strive to work with the simplest hypothesis which can explain all the data satisfactorily.
Similar principles echoed by other luminaries.
Sir Issac Newton: : “We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearances.”
Bertrand Russell: “Whenever possible, substitute constructions out of known entities for inferences to unknown entities.”
Always prefer the shorter hypothesis.
Need an example about what length of a hypothesis is?
Which of the following decision trees have smaller length? A or B?

Even without a precise definition of ‘length’ of a hypothesis, I am sure you would think that the tree on the left (A) looks smaller or shorter. And you will be right, of course. Therefore, a shorter hypothesis is the one which has either less free parameters, or less complex decision boundary (for a classification problem), or some combination of these properties which can represent its brevity.
What about the ‘Length(D|h)’?
It is length of the data given the hypothesis. What does that mean?
Intuitively, it is related to the correctness or representation power of the hypothesis. It governs, among other things, given a hypothesis, how well the data can be ‘inferred’. If the hypothesis generates the data really well and we can measure the data error-free then we don’t need the data at all.
Think of Newton’s laws of motion.
They, when appeared first in Principia, did not have any rigorous mathematical proof behind them. They were not theorems. They were much like hypotheses, based on the observations of the motion of natural bodies. But they described the data really really well. And, consequently they became physical laws.
And that’s why you do not need to maintain and memorize a table of all possible acceleration numbers as a function of force applied to a body. You just trust the compact hypothesis aka law F=ma and believe that all the numbers you need, can just be calculated from it when necessary. It makes the Length(D|h) really small.
But if the data deviates from the compact hypothesis a lot, then you need to have a long descriptions about what these deviations are, possible explanation for them, etc.
Therefore, Length(D|h) is succinctly capturing the notion of “how well the data fits the given hypothesis”.
In essence, it is the notion of misclassification or error rate. For a perfect hypothesis, it is short, zero in the limiting case. For a hypothesis, which does not fit the data perfectly, it tends to be long.
And, there lies the trade-off.
If you shave off your hypothesis with a big Occam’s razor, you will be likely left with a simple model, one which cannot fit all the data. Consequently, you have to supply more data to have better confidence. On the other hand, if you create a complex (and long) hypothesis, you may be able to fit your training data really well but this actually may not be the right hypothesis as it runs against the MAP principle of having a hypothesis with small entropy.
Sounds like a bias-variance trade-off? Yes, also that :-)
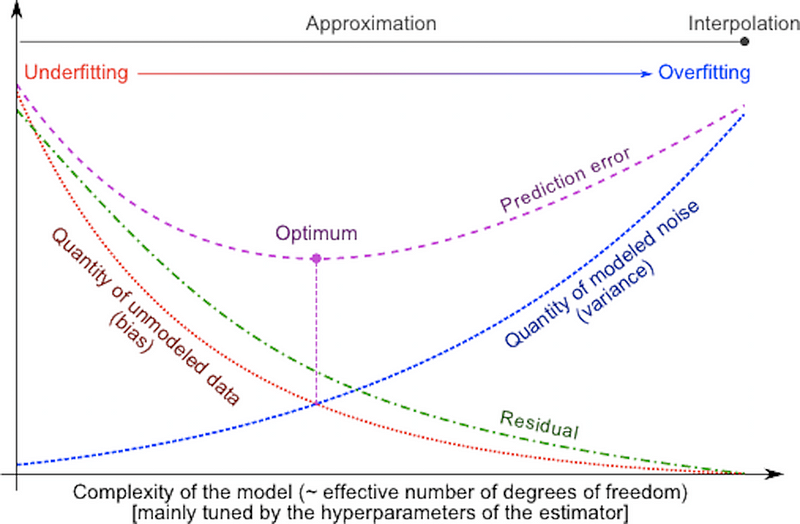
Image source
Putting it all together
Therefore, Bayesian inference tells us that the best hypothesis is the one which minimizes the sum of the two terms: length of the hypothesis and the error rate.
In this one profound sentence, it pretty much captures all of (supervised) machine learning.
Think of its ramifications,
- Model complexity of a linear model— what degree polynomial to choose, how to reduce sum-of-square residuals
- Choice of the architecture of a neural network — how not to overfit the training data and achieve good validation accuracy but reduce the classification error.
- Support vector machine regularization and kernel choice — balance between soft vs. hard margin i.e. trading off accuracy with decision boundary nonlinearity.
What shall we really conclude?
What shall we conclude from this analysis of the Minimum Description
Length (MDL) principle?
Does this prove once and for all that short hypotheses are best?
No.
What MDL shows is that if a representation of hypotheses is chosen so that the size of hypothesis h is — log2 P(h), and if a representation for exceptions (errors) is chosen so that the encoding length of D given h is equal to -log2 P(D|h), then the MDL principle produces MAP hypotheses.
However, to show that we have such a representation we must know all the prior probabilities P(h), as well as the P(D|h). There is no reason to believe that the MDL hypothesis relative to arbitrary encodings of hypothesis and error/misclassification should be preferred.
For practical machine learning, it might sometimes be easier for a human designer to specify a representation that captures knowledge about the relative probabilities of hypotheses than it is to fully specify the probability of each hypothesis.
This is where the matter of knowledge representation and domain expertise become critically important. It short-circuits the (often) infinitely large hypothesis space and leads us towards a highly probable set of hypothesis which we can optimally encode and work towards finding the set of MAP hypotheses among them.
Summary and after-thought
It is a wonderful fact that such a simple set of mathematical manipulations over a basic identity of probability theory can result in such profound and succinct description of the fundamental limitation and goal of supervised machine learning. For a concise treatment of these issue, readers can refer to this Ph.D. thesis, called “Why Machine Learning Works”, from Carnegie Mellon University. It is also worthwhile to ponder over how all of these connect to No-Free-Lunch theorems.
If you are interested in deeper reading in this area
- “No-Free-Lunch and the Minimum Description Length”
- “ No Free Lunch versus Occam’s Razor in Supervised Learning”
- “The No Free Lunch and Problem Description Length”
If you have any questions or ideas to share, please contact the author at tirthajyoti[AT]gmail.com. Also, you can check author’s GitHub repositories for other fun code snippets in Python, R, or MATLAB and machine learning resources. If you are, like me, passionate about machine learning/data science, please feel free to add me on LinkedIn or follow me on Twitter.
Bio: Tirthajyoti Sarkar is a semiconductor technologist, machine learning/data science zealot, Ph.D. in EE, blogger and writer.
Original. Reposted with permission.
Related:
- Essential Math for Data Science: ‘Why’ and ‘How’
- How Much Mathematics Does an IT Engineer Need to Learn to Get Into Data Science?
- Why You Should Forget ‘for-loop’ for Data Science Code and Embrace Vectorization
