How can quantum computing be useful for Machine Learning

comments

By Roger Huang

If you’ve heard of quantum computing, you might be excited about the possibility of applying it to machine learning applications. How can you harness this emerging technology? I work at Springboard, and we recently launched a machine learning bootcamp that includes a job guarantee. We want to make sure our graduates are exposed to cutting-edge machine learning applications -- so we put together this article as part of our research into the intersection of quantum computing and machine learning.

Let’s start by examining the difference between quantum computing and classical computing. In classical computing, your data is stored in physical bits and it is binary and mutually exhaustive: a bit is either in a 0 state or in a 1 state and it cannot be both at the same time. Quantum computing uses the physical properties of smaller-scale physics interactions among molecules so that the quantum bits (called “qubits” for short) can be a linear combination of both a classical 0 and 1 state -- allowing for much more data to be stored in a qubit than in a regular bit.

Quantum computing does suffer from slowdowns, since quantum molecules are entangled with one another, and direct physical observations of the quantum system they are placed in (i.e., trying to get classical results from a quantum computer). But it can process larger amounts of data faster and reduce space/time considerations for many classical computing tasks -- including those related to machine learning.

Let’s now look at some specific instances where quantum computing can help.

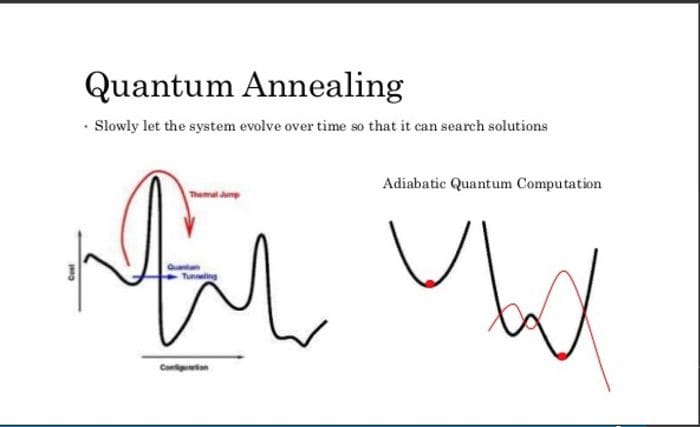
1- Quantum annealers and minimization of loss functions with quantum tunnelling

The first thing to distinguish is between universal gate quantum computers, which can perform every full quantum algorithm (50 or so of which are described in the preceding link) and quantum annealers, which are simplified versions of quantum-capable computers suited to one purpose.

You might be familiar with quantum annealers, such as those from D-Wave. This article goes in-depth in explaining the differences between quantum universal gate computers and annealers. Basically, quantum annealers are “souped-down” versions of universal quantum computers that specialize in finding super-local minima and closer approximations to a global minima than a classical computer.

Source: https://www.slideshare.net/donotstalkme/quantum-computing-55840897

            Quantum annealers work by having a series of magnets attached to a grid. The magnets influence one another and in order for the system as a whole to save energy, they will flip into a coordinated orientation that minimizes energy use. In a classical setting, the magnets get trapped into low-energy settings before being able to find lower minima, but with quantum properties such as tunneling, they can skip those large energy cost settings -- which allows for functions to more easily descend from a local minima into either a global minima or a closer local minima to the global minima.

When it comes to cost functions, this can mean the difference between a gradient descent function being stuck in a sub-optimal setting to one where it is optimal or near-optimal, especially on complex non-convex error surfaces.

They can be a solid solution to a complex machine learning optimization problem if you need a “good enough” answer in a pinch, in a situation that would ordinarily require tons of classical computing power. By exploiting quantum tunneling, you can more quickly converge to minimizing error functions in optimization applications such as portfolio analysis (in finance). This technique has been used to analyze the electrical grid of the United States, with sensors collecting about 3 petabytes of data every two seconds and needing quick loss function calculations almost instantly.

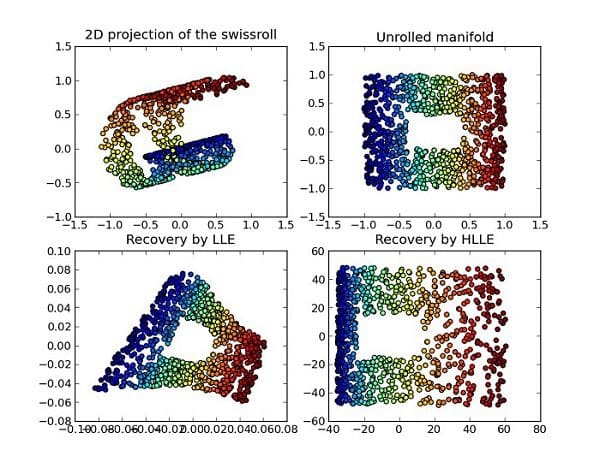
2- Augmenting or replacing support vector machines for dimensionality reduction

            One of the biggest problems in machine learning involves working with calculations in many high-dimensional spaces. In practice, machine learning requires the use of the kernel trick to be able to effectively make calculations. Quantum computers can help make this problem easier: there are quantum interpretations of the SVM kernel trick which can help reduce calculations down to a particular dimension and allow for splitting of high-dimensional datasets into more manageable datasets. This 2016 paper was able to achieve exponential speedups with quantum computers when it came to dimensionality reduction than any algorithm performed on a classical computer.

Source: Wikimedia

With an increase in the number of qubits available, this implementation is growing ever more efficient.

By using a support vector machine implementation that is suited for quantum gates and quantum computing, there is the possibility of classifying very large and complex datasets, such as whether or not cells are cancerous based on a number of factors, at a higher speed and lower computation cost that what currently achievable with classical computers at the moment.

3- Hybrid implementations of small-scale quantum computing and powerful classical computing for very large datasets (ex: topological analysis)

By leveraging the strengths of both quantum computing and classical computing, you can create novel solutions to problems involving huge datasets.

If you wanted to, for example, analyze the topological distribution of your data (conventionally a very hard task, even for smaller datasets) in order to streamline distortions in your data and tangibly weigh the risk of data error, you could use quantum computing, even at a very small scale, to superior effort while using classical computing for the rest of your analysis. This is something academics at MIT, University of Waterloo, and the University of Southern California are actively working on.

By running a topological analysis of a dataset on a quantum computer (when it would be too computationally expensive to do so on a classical computer), you can quickly get all of the significant features in a dataset, gauge its shape and direction and then proceed to do the rest of your work with classical computing algorithms, with the features you need in hand and the proper algorithmic approach

Source: Wikimedia

This sort of approach will allow machine learning algorithms and approaches to be more efficiently implemented in larger and ever-growing datasets with a combination of ever-more powerful quantum and classical computers.

---

Hopefully, this article helped you learn about how to mix quantum algorithms and computing with machine learning. The following course from EdX will help you with practical examples of the two coming together. Coursera offers a selection of courses on quantum computing concepts so you can get more familiar with the space. And if you want to sharpen your machine learning skills or break into a career where you’re doing machine learning full-time and thinking through problems like the ones described above, look no further than Springboard’s AI/Machine Learning Career Track.

Bio: Roger Huang has helped companies multiply their revenue in a matter of weeks, and is now helping people get their dream jobs.

Related:

• Quantum Machine Learning: A look at myths, realities, and future projections
• Age of AI Conference 2018 – Day 2 Highlights
• Quantum Machine Learning: An Overview