Batch Normalization in Deep Neural Networks

By Saurav Singla, Data Scientist

Normalization is a procedure to change the value of the numeric variable in the dataset to a typical scale, without misshaping contrasts in the range of value.

In deep learning, preparing a deep neural network with many layers as they can be delicate to the underlying initial random weights and design of the learning algorithm.

One potential purpose behind this trouble is the distribution of the inputs to layers somewhere down in the network may change after each mini-batch when the weights are refreshed. This can make the learning algorithm always pursue a moving target. This adjustment in the distribution of inputs to layers in the network has alluded to the specialized name internal covariate shift.

Batch normalization is a technique for training very deep neural networks that normalizes the contributions to a layer for every mini-batch. This has the impact of settling the learning process and drastically decreasing the number of training epochs required to train deep neural networks.

One part of this challenge is that the model is refreshed layer-by-layer in reverse from the output to the input utilizing an estimate of error that accept the weights in the layers preceding the current layer are fixed.

Batch normalization gives a rich method of parametrizing practically any deep neural network. The reparameterization fundamentally decreases the issue of planning updates across numerous layers.

It does this scaling the output of the layer, explicitly by normalizing the activations of each input variable per mini-batch, for example, the enactments of a node from the last layer. Review that normalization alludes to rescaling data to have a mean of zero and a standard deviation of one.

 

 

By brightening the inputs to each layer, we would make a stride towards accomplishing the fixed distributions of inputs that would evacuate the ill impacts of the internal covariate shift.

Normalizing the activations of the earlier layer implies that presumptions the ensuing layer makes about the spread and distribution of inputs during the weight update won’t change, in any event not significantly. This has the impact of stabilizing and accelerating the preparation training procedure of deep neural network.

For little smaller mini-batches that don’t contain an agent distribution of models from the training dataset, the distinctions in the normalized inputs among training and inference (utilizing the model subsequent to training) can bring about perceptible contrasts in execution performance. This can be tended to with a change of the technique called Batch Renormalization that makes the appraisals of the variable mean and standard deviation increasingly stable across mini-batches.

This normalization of inputs might be applied to the input variable for the first hidden layer or to the activation from a hidden layer for more profound layers.

It tends to be utilized with most deep network types, for example, Convolutional Neural Networks and Recurrent Neural Networks.

It might be utilized on the inputs to the layer previously or after the activation function in the past layer.

It might be increasingly proper after the activation function if for s-formed capacities like the hyperbolic tangent and logistic function.

It might be fit prior to the activation function for activations that may rise in non-Gaussian scatterings like the rectified linear activation function (ReLU), the front line default for most deep neural network types.

It offers some regularization impact, lessening generalization error, maybe done requiring the utilization of dropout for regularization.

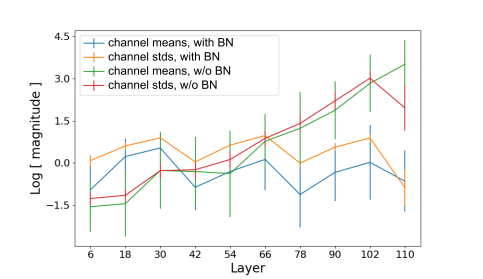
The batch normalized network the mean and variances remain moderately steady all through the network. For an unnormalized network, they seem to develop exponentially with profundity.

 

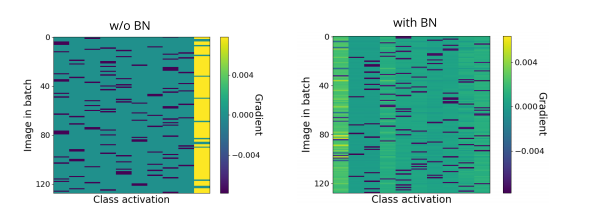
A warmth guide of the yield angles in the last grouping layer after reinstatement. The columns compare to a class and the rows to pictures in the mini-batch. For an unnormalized network, it is apparent that the network reliably predicts one explicit class (extremely right columns), independent of the input. As an outcome, the gradient is exceptionally correlated. For a batch standardized system, the reliance upon the information is a lot bigger.

 

 
Benefits

• The model is less delicate to hyperparameter tuning. That is, though bigger learning rates prompted non-valuable models already, bigger LRs are satisfactory at this point
• Shrinks internal covariant shift
• Diminishes the reliance of gradients on the scale of the parameters or their underlying values
• Weight initialization is a smidgen less significant at this point
• Dropout can be evacuated for regularization

This carries us to the furthest limit of this article where we have found out about Batch normalization and the advantages of utilizing it.

 
Bibliography

• Ioffe, S. and Szegedy, C., 2015. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv:1502.03167
• Santurkar, S., Tsipras, D., Ilyas, A. and Madry, A., 2018. How does batch normalization help optimization?. In Advances in Neural Information Processing Systems (pp. 2483–2493)
• Li, Y., Wang, N., Shi, J., Liu, J. and Hou, X., 2016. Revisiting batch normalization for practical domain adaptation. arXiv preprint arXiv:1603.04779

 
Bio: Saurav Singla is an accomplished and high performing analytical professional with 15 years of deep expertise in the application of analytics, business intelligence, data mining and statistics in multiple industries and 3 years of consulting experience and 5 years of managing a team in the data science field. He is a creative problem solver with a unique mix of technical, business and research proficiency that lends itself to developing key strategies and solutions with a significant impact on revenue and ROI. He possesses working experience in machine learning, statistics, natural language processing and deep learning with extensive use of Python, R, SQL & Tableau.

Original. Reposted with permission.

Related:

• Normalization vs Standardization — Quantitative analysis
• Learning by Forgetting: Deep Neural Networks and the Jennifer Aniston Neuron
• Data Transformation: Standardization vs Normalization