The Key to LLMs: A Mathematical Understanding of Word Embeddings

Image by Author
 

Humans handle text formatting quite intuitively, but with millions of documents generated daily, relying on humans for these tasks is very hard and inefficient. So, the question is, how can we get modern computers to perform tasks like clustering and classification on text data, given that they generally struggle with processing strings meaningfully?

Sure, a computer can compare two strings and determine if they're identical. But how do you teach a computer to understand that "orange" in the sentence "Orange is a tasty fruit" refers to something you can eat rather than a company?

One way to answer this question is to present words that reflect their meaning and the context in which they appear. This can be achieved by using word embeddings, which means a numerical representation of text, allowing a computer to process them efficiently.

In this article, we will examine word embeddings and the mathematical foundations of this groundbreaking method using the very popular algorithm Word2Vec.

 

Word Embeddings

 

In natural language processing (NLP), word embeddings are the digital representation of words. They convert words into numerical vectors—numerical arrays that can be processed with machine learning algorithms.

On a higher level, word embeddings consist of compact vectors that hold continuous values, refined through machine learning methodologies, typically leveraging neural networks. The goal is to create representations that capture word relationships and semantic value. During training, a model is subjected to large amounts of textual input, and its vector representations are refined based on the context in which each word appears.

Let me give you a little example. Consider these vectors as a distinct word's numeric signature. For instance, the word “dog” might be represented by a vector like [0.6, 0.1, 0.5], “cat” is represented as [0.2, -0.4, 0.7], “ orange” is represented as [0.7, -0.1, -0.6], and so on.

If “apple” is numerically close to “fruit” but distant from “car,” the machine recognizes that an apple is more related to fruits than to vehicles. In addition to individual meanings, word embeddings also encode relationships between words. As illustrated in the image below, words frequently appearing together in the same context will have similar or ‘closer’ vectors.

 

This image illustrates the way words that have the same context are closer vectors
 

From the image above, we can deduce that in numerical space, the vectors representing “Russia” and “Moscow” might be closer to each other than those representing “man” and “Russia.” This is because the algorithm has learned from numerous texts that “Russia” and “Moscow” often appear in similar settings, such as discussions about countries and capitals. At the same time “man” and “Russia” do not.

Many algorithms are used to create word embeddings, and each one takes a different approach to capturing the semantic meanings and relationships between words. The next section will examine one of these algorithms.

 

Word2Vec (Word to Vector)

 

Word2Vec transforms each word in our vocabulary into a vector representation. Words that appear in similar contexts or share semantic relationships are represented by vectors close to each other in the vector space, meaning that similar words will have similar vectors. A team of Google researchers led by Tomas Mikolov created, patented, and released Word2Vec in 2013.

 

Understanding the neural network training of the Word2Vec model | Source
 

• All of the texts or documents in our training set make up the input. These texts are turned into a one-hot encoding of the words so that the network can process them
• The neurons in the hidden layer line up with the word vectors' intended length. For instance, the hidden layer will have 300 neurons if we want the word vectors to have a length of 300 neurons
• The output layer predicts the predicted word by generating probability for a target word based on the input
• The word embeddings in the hidden layer are the weights following training. In essence, a series of weights (300 in this case) that represent different facets of the word are assigned to each word

Word2Vec has two primary architectures: Skip-gram and Continuous Bag of Words (CBOW).

 

Continuous Bag of Words (CBOW)

 
The CBOW model predicts a target word based on its context words. Given a sequence of words {w1, w2 ,…, wT}, and a context window of size m, CBOW aims to predict the word wt using the context words {wt−m ,…, wt−1, wt+1 ,…, wt+m}.

Objective Function:

The objective function in the CBOW model aims to maximize the probability of correctly predicting the target word given its context. It can be expressed as:

 

The objective function in the CBOW model
 

Where:

• T is the total number of words in the corpus
• m is the size of the context window
• w_t​ is the target word
• w_{t−m,…,wt−1,wt+1,…,wt+m} are the context words
• P(w_t ∣ ⋅) is the conditional probability of the target word given the context

Conditional Probability:

The conditional probability P(w_t ∣ w_t−m,…,w_t−1,w_t+1,…,w_t+m) represents the likelihood of the target word w_t​ given the context words. It is calculated using the softmax function, which normalizes the scores into a probability distribution:

 

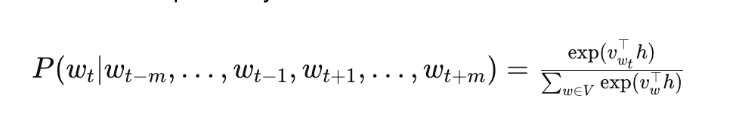
The Conditional Probability in the CBOW model
 

Where:

• v_wt​ is the output vector of the target word w_t​
• h is the hidden layer representation (context vector)
• V is the vocabulary

Hidden Layer:

The hidden layer h in the CBOW model is calculated as the mean of the context word input vectors. This hidden layer provides the overall representation of the context:

 

The Hidden Layer in the CBOW model
 

Where:

• v_{wt+j​​ are the input vectors for the context words}
• The summation goes over the context window, excluding the target word itself

This averaging process creates a single vector that captures the overall meaning of the context words.

Softmax Function:

The softmax function is used to convert the raw scores (dot products of the target word vector and the hidden layer vector) into a probability distribution over the vocabulary:

 

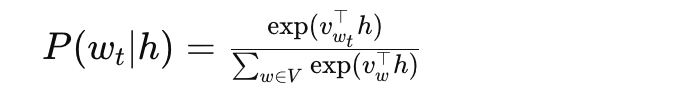
The Softmax Function in the CBOW model
 

Where:

• exp⁡(⋅) denotes the exponential function
• w^⊤_{wt​ ​h is the dot product between the output vector of the target word and the hidden layer vector}
• The denominator sums the exponentiated dot products for all words in the vocabulary V, ensuring that the output is a valid probability distribution

 

Skip-gram

 
The Skip-gram model works in the reverse manner of CBOW. It predicts the context words given a target word. Given a target word wt​, Skip-gram predicts the context words {wt−m,…,wt−1,wt+1,…,wt+m}.

Objective Function:

The Skip-gram's objective function establishes the model's training aim. It gauges how well the algorithm forecasts context words in the presence of a target word. Skip-gram aims to maximize the probability of observing context words wt+j​ given a target word wt​.

 

The Objective Function in the Skip-gram model
 

Where:

• T is the total number of words in the corpus
• θ represents the parameters of the model, which include the input and output word vectors

Conditional Probability:

The conditional probability P(wt+j ∣ wt;θ) in Skip-gram specifies the likelihood of observing the context word wt+j​ given the target word wt​ and the model parameters θ.

 

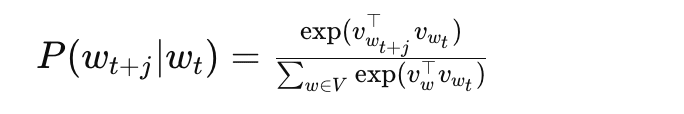
The Conditional Probability in the Skip-gram model
 

Where:

• v_wt​​ is the input vector of the target word w_t​
• v_wt+j​​ is the output vector (word embedding) of the context word w_t+j​

Softmax Function:

The softmax function is used to compute the conditional probabilities P(wt+j ∣ wt;θ) for all words in the vocabulary V. It converts raw scores (dot products) into probabilities.

 

The Softmax Function in the Skip-gram model
 

The softmax function is essential because it ensures that the predicted probabilities are non-negative and sum to 1, making them suitable for a probabilistic interpretation. During training, the model adjusts the parameters θ (word embeddings) to maximize the likelihood of observing the actual context words given the target words in the corpus.

 

Benefits of Word2Vec

 
The following are some advantages of Word2Vec for word embeddings.

1. By encoding semantic meanings, Word2Vec embeddings enable computers to comprehend words in light of their context and connections with other words within a corpus
2. Word2Vec produces compact, dense vector representations that effectively capture language patterns and similarities in contrast to conventional one-hot encoding
3. Because Word2Vec provides better contextual knowledge, applications that use it frequently find improvements in performance in tasks like sentiment analysis, document clustering, and machine translation
4. Many NLP projects may be started with pre-trained Word2Vec models, which eliminates the requirement for a lot of task-specific training data
5. Word2Vec is language-agnostic to some extent, meaning the same principles can be applied across different languages, adapting to various linguistic structures and vocabularies

 

Conclusion

 
Research on word embeddings is still active and aims to improve word representations beyond what is considered good. In this article, some of the mathematical foundations of word embeddings were made more understandable.

We looked at Word2Vec, a solid method that abstracts words into numerical vectors so that computers can understand natural language. The secret of Word2Vec's efficacy is its capacity to recognize word structural and semantic similarities. It uses architectures suited to various datasets and goals, such as CBOW and Skip-Gram.

For further reading, check out these resources:

• Mikolov et al., 2013, Efficient estimation of word representations in vector space
• Mikolov et al., 2013, Distributed Representations of Words and Phrases and their Compositionality
• The Illustrated Word2vec
• Distributed Representations of Words and Phrases and their Compositionality
• A Neural Probabilistic Language Model
• Efficient Estimation of Word Representations in Vector Space

 
 

Shittu Olumide is a software engineer and technical writer passionate about leveraging cutting-edge technologies to craft compelling narratives, with a keen eye for detail and a knack for simplifying complex concepts. You can also find Shittu on Twitter.