Why Does Deep Learning Not Have a Local Minimum?

comments

By Charles H Martin, Calculation Consulting.

Editor's note: This post originally appeared as an answer to a Quora question, which also included the following:

"As I understand, the chance of having a derivative zero in each of the thousands of direction is low. Is there some other reason besides this?"

Yes, there is a ‘theoretical justification’, and has taken a couple decades to flush it out.

I will first point out, however, it has been observed in practice. This was pointed out by LeCun in his early work on LeNet, and is actually discussed in the ‘orange book’, “Pattern Classification” by David G. Stork, Peter E. Hart, and Richard O. Duda.

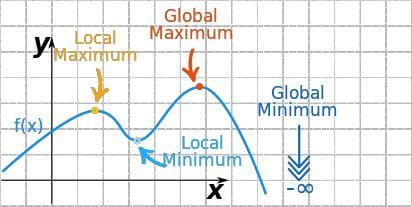
Source: Maxima and Minima of Functions.

The problem has been addressed in condensed matter physics 20 years ago in the study of spin glasses.

The basic program was first developed by Parisi, in an approximate, non-rigorous form:

On the stationary points of the TAP free energy

and then, later, proven exact using methods from Random Matrix Theory. It is this result that LeCun is talking about:

Critical Points in High Dimensional Landscapes

I will outline Parisi’s general approach:

He studied a specific kind of random Hamiltonian — a mean field spin glass called the p-spin spherical spin glass. He then:

1. finds an analytical expression for the TAP Free Energy (at T>0). The TAP (Thouless Anderson Palmer) theory is a general approach to spin glasses, and can even be applied to RBMs: (see Improving RBMs with physical chemistry)
2. computes the configurational entropy, and, additionally, a complexity metric — which counts the number of critical / saddle points . This was done using techniques from statistical field theory.
3. extends this result to the T=0 Energy Landscape, in order to count the number of critical points, at a specific energy level E. The general result by Parisi showed that the all of the local minima ‘concentrated (in the statistical sense)’ in a small band slightly above the global ground state

What is usually never explained is why in the world this is an important problem in the study of spin glasses and why the p-spin-spherical spin glass is the right object to study, apart from it being a solved model, albeit with a lot of hard assumptions, that Deep Learning researchers can draw upon. Additionally, in deep learning, there is no distinction between the T=0 Energy Landscape and the T>0 Free Energy Landscape, even though traditionally methods like RBMs and VAEs are operate implicitly at T=1.

There are more recent results which attempt to address deep learning directly:

Deep Learning without Poor Local Minima

which further suggests the SGD solvers can not actually distinguish between saddle points and local minima because the Hessian is very ill-conditioned. This is confirmed by recent numerical work by LeCun, that shows Hessian does indeed have many zeros:

Biasing Gradient Descent Into Wide Valleys

I personally don’t think this is the whole picture, and there has been extensive work on this class of problems by physical chemists such as Peter Wolynes. The issue is related to a very puzzling phenomena in the theory of super cooled glasses called the Adam-Gibbs phenomena and the related Entropy Crisis that occurs in real, structural glasses. The subject is very deep, but suffice it to say that the reason the p-spin spherical spin glass is interesting is that it is a simple spin-glass model, with a real energy landscape, that shows an entropy crisis. In fact, I conjecture that deep nets would also display an entropy crisis — i.e. they run out of configurational entropy — when they overtrained.

This Entropy crisis, resulting in overtraining, would look like a sharp valley because it has run out of configurational entropy, and is analogous to what LeCun is talking about in his work on Entropy-SGD. And it has very recently recently observed in RBMs:

[1612.01717] Statistical mechanics of unsupervised feature learning in a restricted Boltzmann machine with binary synapses

These kinds of funneled landscapes are known from protein folding:

Why does Deep Learning work?

I address some these issues in my 2016 Summer Talk At MDDS at UC Berkeley.

Bio: Charles H Martin, PhD, is a Data Scientist & Machine Learning Expert in San Francisco Bay Area, currently with Calculation Consulting.

Original. Reposted with permission.

Related:

• Why Does Deep Learning Work?
• Three Impactful Machine Learning Topics at ICML 2016
• Why Deep Learning Works – Key Insights and Saddle Points