21 Must-Know Data Science Interview Questions and Answers, part 2
Second part of the answers to 20 Questions to Detect Fake Data Scientists, including controlling overfitting, experimental design, tall and wide data, understanding the validity of statistics in the media, and more.
The post on KDnuggets
20 Questions to Detect Fake Data Scientists has been very popular - most viewed post of the month.
However these questions were lacking answers, so KDnuggets Editors got together and wrote the answers. Here is part 2 of the answers, starting with a "bonus" question.
This question was not part of the original 20, but probably is the most important one in distinguishing real data scientists from fake ones.
Answer by Gregory Piatetsky.
Overfitting is finding spurious results that are due to chance and cannot be reproduced by subsequent studies.
We frequently see newspaper reports about studies that overturn the previous findings, like eggs are no longer bad for your health, or saturated fat is not linked to heart disease. The problem, in our opinion is that many researchers, especially in social sciences or medicine, too frequently commit the cardinal sin of Data Mining - Overfitting the data.
The researchers test too many hypotheses without proper statistical control, until they happen to find something interesting and report it. Not surprisingly, next time the effect, which was (at least partly) due to chance, will be much smaller or absent.
These flaws of research practices were identified and reported by John P. A. Ioannidis in his landmark paper Why Most Published Research Findings Are False (PLoS Medicine, 2005). Ioannidis found that very often either the results were exaggerated or the findings could not be replicated. In his paper, he presented statistical evidence that indeed most claimed research findings are false.
Ioannidis noted that in order for a research finding to be reliable, it should have:
Unfortunately, too often these rules were violated, producing irreproducible results. For example, S&P 500 index was found to be strongly related to Production of butter in Bangladesh (from 19891 to 1993) (here is PDF)

See more interesting (and totally spurious) findings which you can discover yourself using tools such as Google correlate or Spurious correlations by Tyler Vigen.
Several methods can be used to avoid "overfitting" the data
Good data science is on the leading edge of scientific understanding of the world, and it is data scientists responsibility to avoid overfitting data and educate the public and the media on the dangers of bad data analysis.
See also
Answer by Bhavya Geethika.
Step 1: Formulate the Research Question:
What are the effects of page load times on user satisfaction ratings?
Step 2: Identify variables:
We identify the cause & effect. Independent variable -page load time, Dependent variable- user satisfaction rating
Step 3: Generate Hypothesis:
Lower page download time will have more effect on the user satisfaction rating for a web page. Here the factor we analyze is page load time.

Fig 12: There is a flaw in your experimental design (cartoon from here)
Step 4: Determine Experimental Design.
We consider experimental complexity i.e vary one factor at a time or multiple factors at one time in which case we use factorial design (2^k design). A design is also selected based on the type of objective (Comparative, Screening, Response surface) & number of factors.
Here we also identify within-participants, between-participants, and mixed model.For e.g.: There are two versions of a page, one with Buy button (call to action) on left and the other version has this button on the right.
Within-participants design - both user groups see both versions.
Between-participants design - one group of users see version A & the other user group version B.
Step 5: Develop experimental task & procedure:
Detailed description of steps involved in the experiment, tools used to measure user behavior, goals and success metrics should be defined. Collect qualitative data about user engagement to allow statistical analysis.
Step 6: Determine Manipulation & Measurements
Manipulation: One level of factor will be controlled and the other will be manipulated. We also identify the behavioral measures:
Step 7: Analyze results
Identify user behavior data and support the hypothesis or contradict according to the observations made for e.g. how majority of users satisfaction ratings compared with page load times.
Answer by Gregory Piatetsky.
In most data mining / data science applications there are many more records (rows) than features (columns) - such data is sometimes called "tall" (or "long") data.
In some applications like genomics or bioinformatics you may have only a small number of records (patients), eg 100, but perhaps 20,000 observations for each patient. The standard methods that work for "tall" data will lead to overfitting the data, so special approaches are needed.

Fig 13. Different approaches for tall data and wide data, from presentation Sparse Screening for Exact Data Reduction, by Jieping Ye.
The problem is not just reshaping the data (here there are useful R packages), but avoiding false positives by reducing the number of features to find most relevant ones.
Approaches for feature reduction like Lasso are well covered in Statistical Learning with Sparsity: The Lasso and Generalizations, by Hastie, Tibshirani, and Wainwright. (you can download free PDF of the book)
However these questions were lacking answers, so KDnuggets Editors got together and wrote the answers. Here is part 2 of the answers, starting with a "bonus" question.
Bonus Question: Explain what is overfitting and how would you control for it
This question was not part of the original 20, but probably is the most important one in distinguishing real data scientists from fake ones.
Answer by Gregory Piatetsky.
Overfitting is finding spurious results that are due to chance and cannot be reproduced by subsequent studies.
We frequently see newspaper reports about studies that overturn the previous findings, like eggs are no longer bad for your health, or saturated fat is not linked to heart disease. The problem, in our opinion is that many researchers, especially in social sciences or medicine, too frequently commit the cardinal sin of Data Mining - Overfitting the data.
The researchers test too many hypotheses without proper statistical control, until they happen to find something interesting and report it. Not surprisingly, next time the effect, which was (at least partly) due to chance, will be much smaller or absent.
These flaws of research practices were identified and reported by John P. A. Ioannidis in his landmark paper Why Most Published Research Findings Are False (PLoS Medicine, 2005). Ioannidis found that very often either the results were exaggerated or the findings could not be replicated. In his paper, he presented statistical evidence that indeed most claimed research findings are false.
Ioannidis noted that in order for a research finding to be reliable, it should have:
- Large sample size and with large effects
- Greater number of and lesser selection of tested relationship
- Greater flexibility in designs, definitions, outcomes, and analytical modes
- Minimal bias due to financial and other factors (including popularity of that scientific field)
Unfortunately, too often these rules were violated, producing irreproducible results. For example, S&P 500 index was found to be strongly related to Production of butter in Bangladesh (from 19891 to 1993) (here is PDF)
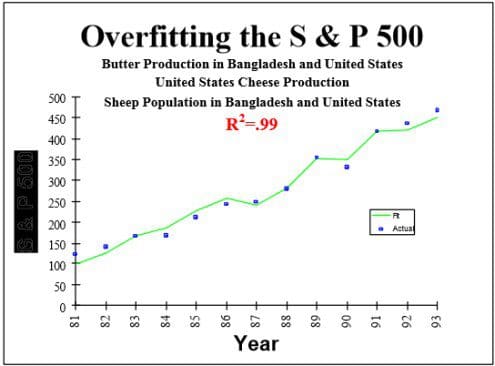
See more interesting (and totally spurious) findings which you can discover yourself using tools such as Google correlate or Spurious correlations by Tyler Vigen.
Several methods can be used to avoid "overfitting" the data
- Try to find the simplest possible hypothesis
- Regularization (adding a penalty for complexity)
- Randomization Testing (randomize the class variable, try your method on this data - if it find the same strong results, something is wrong)
- Nested cross-validation (do feature selection on one level, then run entire method in cross-validation on outer level)
- Adjusting the False Discovery Rate
- Using the reusable holdout method - a breakthrough approach proposed in 2015
Good data science is on the leading edge of scientific understanding of the world, and it is data scientists responsibility to avoid overfitting data and educate the public and the media on the dangers of bad data analysis.
See also
- The Cardinal Sin of Data Mining and Data Science: Overfitting
- Big Idea To Avoid Overfitting: Reusable Holdout to Preserve Validity in Adaptive Data Analysis
- Overcoming Overfitting with the reusable holdout: Preserving validity in adaptive data analysis
- 11 Clever Methods of Overfitting and how to avoid them
- Tag: Overfitting
Q12. Give an example of how you would use experimental design to answer a question about user behavior.
Answer by Bhavya Geethika.
Step 1: Formulate the Research Question:
What are the effects of page load times on user satisfaction ratings?
Step 2: Identify variables:
We identify the cause & effect. Independent variable -page load time, Dependent variable- user satisfaction rating
Step 3: Generate Hypothesis:
Lower page download time will have more effect on the user satisfaction rating for a web page. Here the factor we analyze is page load time.

Fig 12: There is a flaw in your experimental design (cartoon from here)
Step 4: Determine Experimental Design.
We consider experimental complexity i.e vary one factor at a time or multiple factors at one time in which case we use factorial design (2^k design). A design is also selected based on the type of objective (Comparative, Screening, Response surface) & number of factors.
Here we also identify within-participants, between-participants, and mixed model.For e.g.: There are two versions of a page, one with Buy button (call to action) on left and the other version has this button on the right.
Within-participants design - both user groups see both versions.
Between-participants design - one group of users see version A & the other user group version B.
Step 5: Develop experimental task & procedure:
Detailed description of steps involved in the experiment, tools used to measure user behavior, goals and success metrics should be defined. Collect qualitative data about user engagement to allow statistical analysis.
Step 6: Determine Manipulation & Measurements
Manipulation: One level of factor will be controlled and the other will be manipulated. We also identify the behavioral measures:
- Latency- time between a prompt and occurrence of behavior (how long it takes for a user to click buy after being presented with products).
- Frequency- number of times a behavior occurs (number of times the user clicks on a given page within a time)
- Duration-length of time a specific behavior lasts(time taken to add all products)
- Intensity-force with which a behavior occurs ( how quickly the user purchased a product)
Step 7: Analyze results
Identify user behavior data and support the hypothesis or contradict according to the observations made for e.g. how majority of users satisfaction ratings compared with page load times.
Q13. What is the difference between "long" ("tall") and "wide" format data?
Answer by Gregory Piatetsky.
In most data mining / data science applications there are many more records (rows) than features (columns) - such data is sometimes called "tall" (or "long") data.
In some applications like genomics or bioinformatics you may have only a small number of records (patients), eg 100, but perhaps 20,000 observations for each patient. The standard methods that work for "tall" data will lead to overfitting the data, so special approaches are needed.

Fig 13. Different approaches for tall data and wide data, from presentation Sparse Screening for Exact Data Reduction, by Jieping Ye.
The problem is not just reshaping the data (here there are useful R packages), but avoiding false positives by reducing the number of features to find most relevant ones.
Approaches for feature reduction like Lasso are well covered in Statistical Learning with Sparsity: The Lasso and Generalizations, by Hastie, Tibshirani, and Wainwright. (you can download free PDF of the book)
