Nutrition & Principal Component Analysis: A Tutorial
A great overview of Principal Component Analysis (PCA), with an example application in the field of nutrition.
The Problem
Imagine that you are a nutritionist trying to explore the nutritional content of food. What is the best way to differentiate food items? By vitamin content? Protein levels? Or perhaps a combination of both?

Knowing the variables that best differentiate your items has several uses:
1. Visualization. Using the right variables to plot items will give more insights.
2. Uncovering Clusters. With good visualizations, hidden categories or clusters could be identified. Among food items for instance, we may identify broad categories like meat and vegetables, as well as sub-categories such as types of vegetables.
The question is, how do we derive the variables that best differentiate items?
Definition
Principal Components Analysis (PCA) is a technique that finds underlying variables (known as principal components) that best differentiate your data points. Principal components are dimensions along which your data points are most spread out:
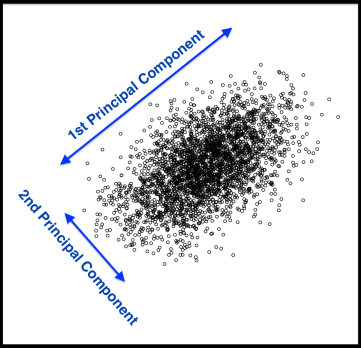
A principal component can be expressed by one or more existing variables. For example, we may use a single variable – vitamin C – to differentiate food items. Because vitamin C is present in vegetables but absent in meat, the resulting plot (below, left) will differentiate vegetables from meat, but meat items will clumped together.
To spread the meat items out, we can use fat content in addition to vitamin C levels, since fat is present in meat but absent in vegetables. However, fat and vitamin C levels are measured in different units. So to combine the two variables, we first have to normalize them, meaning to shift them onto a uniform standard scale, which would allow us to calculate a new variable – vitamin C minus fat. Combining the two variables helps to spread out both vegetable and meat items.
The spread can be further improved by adding fiber, of which vegetable items have varying levels. This new variable – (vitamin C + fiber) minus fat – achieves the best data spread yet.

While in this demonstration we tried to derive principal components by trial-and-error, PCA does this by systematic computation.
