How Convolutional Neural Networks Work
Get an overview of what is going on inside convolutional neural networks, and what it is that makes them so effective.
Rectified Linear Units
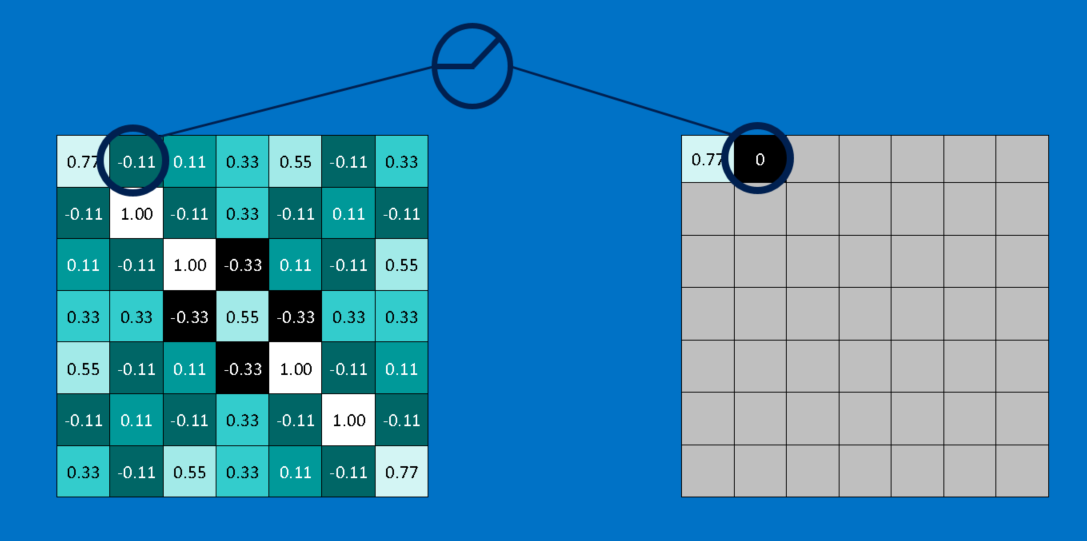
A small but important player in this process is the Rectified Linear Unit or ReLU. It’s math is also very simple—wherever a negative number occurs, swap it out for a 0. This helps the CNN stay mathematically healthy by keeping learned values from getting stuck near 0 or blowing up toward infinity. It’s the axle grease of CNNs—not particularly glamorous, but without it they don’t get very far.
The output of a ReLU layer is the same size as whatever is put into it, just with all the negative values removed.
Deep learning
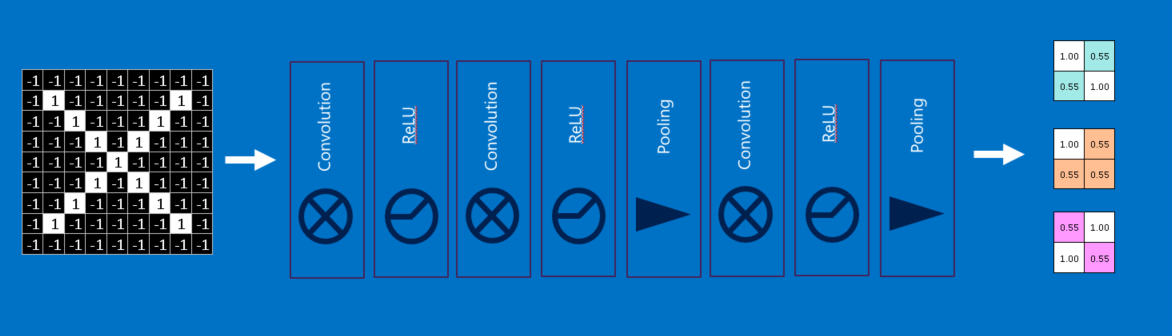
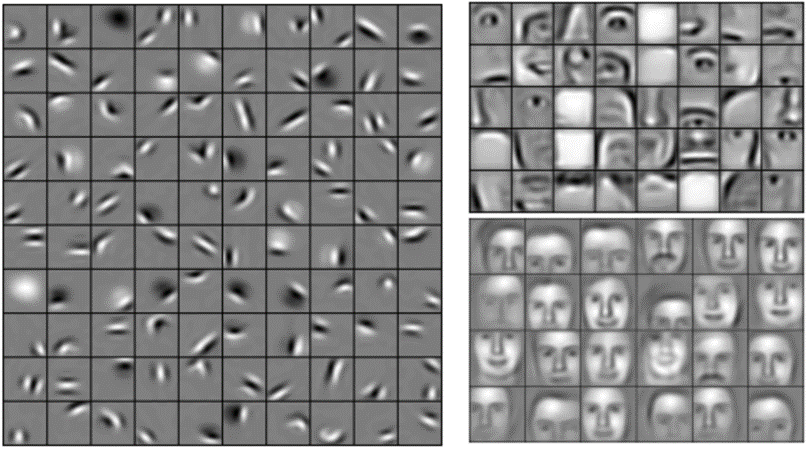
You’ve probably noticed that the input to each layer (two-dimensional arrays) looks a lot like the output (two-dimensional arrays). Because of this, we can stack them like Lego bricks. Raw images get filtered, rectified and pooled to create a set of shrunken, feature-filtered images. These can be filtered and shrunken again and again. Each time, the features become larger and more complex, and the images become more compact. This lets lower layers represent simple aspects of the image, such as edges and bright spots. Higher layers can represent increasingly sophisticated aspects of the image, such as shapes and patterns. These tend to be readily recognizable. For instance, in a CNN trained on human faces, the highest layers represent patterns that are clearly face-like. (1)
Fully connected layers
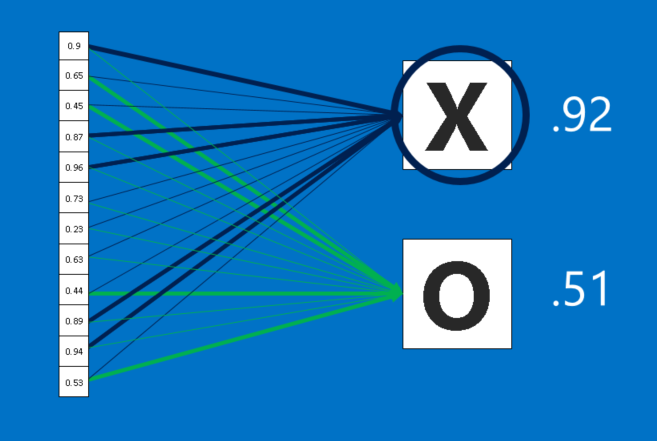
CNNs have one more arrow in their quiver. Fully connected layers take the high-level filtered images and translate them into votes. In our case, we only have to decide between two categories, X and O. Fully connected layers are the primary building block of traditional neural networks. Instead of treating inputs as a two-dimensional array, they are treated as a single list and all treated identically. Every value gets its own vote on whether the current image is an X or and O. However, the process isn’t entirely democratic. Some values are much better than others at knowing when the image is an X, and some are particularly good at knowing when the image is an O. These get larger votes than the others. These votes are expressed as weights, or connection strengths, between each value and each category.
When a new image is presented to the CNN, it percolates through the lower layers until it reaches the fully connected layer at the end. Then an election is held. The answer with the most votes wins and is declared the category of the input.
Fully connected layers, like the rest, can be stacked because their outputs (a list of votes) look a whole lot like their inputs (a list of values). In practice, several fully connected layers are often stacked together, with each intermediate layer voting on phantom “hidden” categories. In effect, each additional layer lets the network learn ever more sophisticated combinations of features that help it make better decisions.
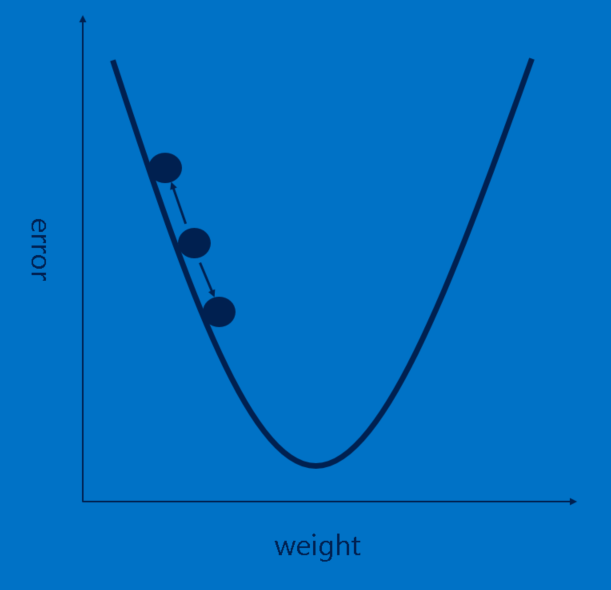
Backpropagation
Our story is filling in nicely, but it still has a huge hole—Where do features come from? and How do we find the weights in our fully connected layers? If these all had to be chosen by hand, CNNs would be a good deal less popular than they are. Luckily, a bit of machine learning magic called backpropagation does this work for us.
To make use of backpropagation, we need a collection of images that we already know the answer for. This means that some patient soul flipped through thousands of images and assigned them a label of X or O. We use these with an untrained CNN, which means that every pixel of every feature and every weight in every fully connected layer is set to a random value. Then we start feeding images through it, one after other.
Each image the CNN processes results in a vote. The amount of wrongness in the vote, the error, tells us how good our features and weights are. The features and weights can then be adjusted to make the error less. Each value is adjusted a little higher and a little lower, and the new error computed each time. Whichever adjustment makes the error less is kept. After doing this for every feature pixel in every convolutional layer and every weight in every fully connected layer, the new weights give an answer that works slightly better for that image. This is then repeated with each subsequent image in the set of labeled images. Quirks that occur in a single image are quickly forgotten, but patterns that occur in lots of images get baked into the features and connection weights. If you have enough labeled images, these values stabilize to a set that works pretty well across a wide variety of cases.
As is probably apparent, backpropagation is another expensive computing step, and another motivator for specialized computing hardware.
Hyperparameters
Unfortunately, not every aspect of CNNs can be learned in so straightforward a manner. There is still a long list of decisions that a CNN designer must make.
- For each convolution layer, How many features? How many pixels in each feature?
- For each pooling layer, What window size? What stride?
- For each extra fully connected layer, How many hidden neurons?
In addition to these there are also higher level architectural decisions to make: How many of each layer to include? In what order? Some deep neural networks can have over a thousand layers, which opens up a lot of possibilities.
With so many combinations and permutations, only a small fraction of the possible CNN configurations have been tested. CNN designs tend to be driven by accumulated community knowledge, with occasional deviations showing surprising jumps in performance. And while we’ve covered the building blocks of vanilla CNNs, there are lots of other tweaks that have been tried and found effective, such as new layer types and more complex ways to connect layers with each other.
Beyond images
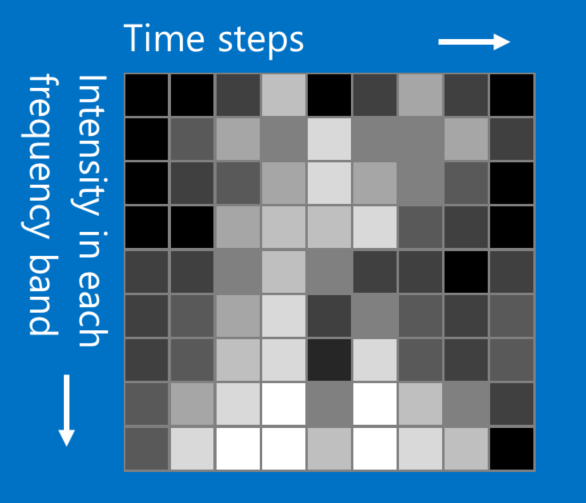
While our X and O example involves images, CNNs can be used to categorize other types of data too. The trick is, whatever data type you start with, to transform it to make it look like an image. For instance, audio signals can be chopped into short time chunks, and then each chunk broken up into bass, midrange, treble, or finer frequency bands. This can be represented as a two-dimensional array where each column is a time chunk and each row is a frequency band. “Pixels” in this fake picture that are close together are closely related. CNNs work well on this. Researchers have gotten quite creative. They have adapted text data for natural language processing and even chemical data for drug discovery.
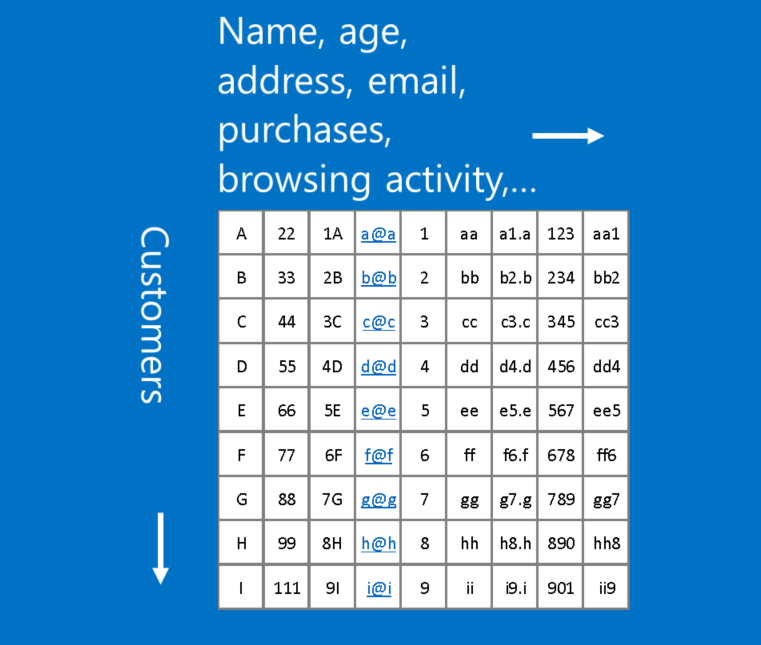
An example of data that doesn’t fit this format is customer data, where each row in a table represents a customer, and each column represents information about them, such as name, address, email, purchases and browsing history. In this case, the location of rows and columns doesn’t really matter. Rows can be rearranged and columns can be re-ordered without losing any of the usefulness of the data. In contrast, rearranging the rows and columns of an image makes it largely useless.
A rule of thumb: If your data is just as useful after swapping any of your columns with each other, then you can’t use Convolutional Neural Networks.
However if you can make your problem look like finding patterns in an image, then CNNs may be exactly what you need.
Learn more
If you'd like to dig deeper into deep learning, check out my Demystifying Deep Learning post. I also recommend the notes from the Stanford CS 231 course by Justin Johnson and Andrej Karpathy that provided inspiration for this post, as well as the writings ofChristopher Olah, an exceptionally clear writer on the subject of neural networks.
If you are one who loves to learn by doing, there are a number of popular deep learning tools available. Try them all! And then tell us what you think.
I hope you've enjoyed our walk through the neighborhood of Convolutional Neural Networks. Feel free to start up a conversation publicly or in a personal message.
Brandon
@_brohrer_
Facebook
LinkedIn
If you found this helpful, I also recommend the Data Science and Robots Blog. I work at Microsoft, but my opinions are my own.
Original. Reposted with permission.
Related: