 Random Forests®, Explained
Random Forests®, Explained
Random Forest, one of the most popular and powerful ensemble method used today in Machine Learning. This post is an introduction to such algorithm and provides a brief overview of its inner workings.
In this post, we will give an overview of a very popular ensemble method called Random Forests(®). We first discuss the fundamental components of this ensemble learning algorithm - Decision Trees - and then the underlying algorithm and training procedures. We will also discuss some variations and advantages of this tool, and finally provide resources for you to get started with this powerful tool.
Decision Trees in a Nutshell
A decision tree is a Machine Learning algorithm capable of fitting complex datasets and performing both classification and regression tasks. The idea behind a tree is to search for a pair of variable-value within the training set and split it in such a way that will generate the "best" two child subsets. The goal is to create branches and leafs based on an optimal splitting criteria, a process called tree growing. Specifically, at every branch or node, a conditional statement classifies the data point based on a fixed threshold in a specific variable, therefore splitting the data. To make predictions, every new instance starts in the root node (top of the tree) and moves along the branches until it reaches a leaf node where no further branching is possible.
The algorithm used to train a tree is called CART(®) (Classification And Regression Tree). As we already mentioned, the algorithm seeks the best feature–value pair to create nodes and branches. After each split, this task is performed recursively until the maximum depth of the tree is reached or an optimal tree is found. Depending on the task, the algorithm may use a different metric (Gini impurity, information gain or mean square error) to measure the quality of the split. It is important to mention that due to the greedy nature of the CART algorithm, finding an optimal tree is not guaranteed and usually, a reasonably good estimation will suffice.
Trees have a high risk of overfitting the training data as well as becoming computationally complex if they are not constrained and regularized properly during the growing stage. This overfitting implies a low bias, high variance trade-off in the model. Therefore, in order to deal with this problem, we use Ensemble Learning, an approach that allows us to correct this overlearning habit and hopefully, arrive at better, stronger results.
What is an Ensemble Method?
An ensemble method or ensemble learning algorithm consists of aggregating multiple outputs made by a diverse set of predictors to obtain better results. Formally, based on a set of “weak” learners we are trying to use a “strong” learner for our model. Therefore, the purpose of using ensemble methods is: to average out the outcome of individual predictions by diversifying the set of predictors, thus lowering the variance, to arrive at a powerful prediction model that reduces overfitting our training set.
In our case, a Random Forest (strong learner) is built as an ensemble of Decision Trees (weak learners) to perform different tasks such as regression and classification.

How are Random Forests trained?
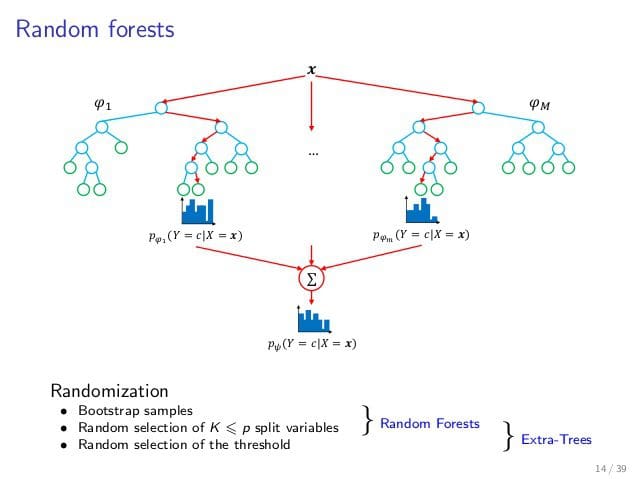
Random Forests are trained via the bagging method. Bagging or Bootstrap Aggregating, consists of randomly sampling subsets of the training data, fitting a model to these smaller data sets, and aggregating the predictions. This method allows several instances to be used repeatedly for the training stage given that we are sampling with replacement. Tree bagging consists of sampling subsets of the training set, fitting a Decision Tree to each, and aggregating their result.
The Random Forest method introduces more randomness and diversity by applying the bagging method to the feature space. That is, instead of searching greedily for the best predictors to create branches, it randomly samples elements of the predictor space, thus adding more diversity and reducing the variance of the trees at the cost of equal or higher bias. This process is also known as “feature bagging” and it is this powerful method what leads to a more robust model.
Let’s see now how to make predictions with Random Forests. Remember that in a Decision Tree a new instance goes from the root node to the bottom until it is classified in a leaf node. In the Random Forests algorithm, each new data point goes through the same process, but now it visits all the different trees in the ensemble, which are were grown using random samples of both training data and features. Depending on the task at hand, the functions used for aggregation will differ. For Classification problems, it uses the mode or most frequent class predicted by the individual trees (also known as a majority vote), whereas for Regression tasks, it uses the average prediction of each tree.
Although this is a powerful and accurate method used in Machine Learning, you should always cross-validate your model as there may be overfitting. Also, despite its robustness, the Random Forest algorithm is slow, as it has to grow many trees during training stage and as we already know, this is a greedy process.
Variations
As we already specified, a Random Forest uses sampled subsets of both the training data and the feature space, which result in high diversity and randomness as well as low variance. Now, we can go a step further and introduce a bit more variety by not only looking for a random predictor but also considering random thresholds for each of these variables. Therefore, instead of looking for the optimal pair of feature and threshold for the splitting, it uses random samples of both to create the different branches and nodes, thus further trading variance for bias. This ensemble is also known as Extremely Randomized Trees or Extra-Trees. This model also trades more bias for a lower variance but it is faster to train as it is not looking for an optimum, like the case of Random Forests.
Additional Properties
One other important attribute of Random Forests is that they are very useful when trying to determine feature or variable importance. Because important features tend to be at the top of each tree and unimportant variables are located near the bottom, one can measure the average depth at which this
Further Information
You may find more information about Random Forests in this Wikipedia article. The Johns Hopkins University Coursera's course on Practical Machine Learning has a nice intuitive approach with applications in R. For a Python implementation, follow the code by Aurélien Géron from his book "Hands-On Machine Learning with Scikit-Learn and TensorFlow".
Random Forests™ is a trademark of Leo Breiman and Adele Cutler and is licensed exclusively to Salford Systems for the commercial release of the software. CART(®) is a registered trademark of California Statistical Software, Inc. and is exclusively licensed to Salford Systems.
Related Content

 Random Forests®, Explained
Random Forests®, Explained