Multiscale Methods and Machine Learning

comments

Multiscale methods, in which a dataset is viewed and analyzed at different scales,are becoming more commonplace in machine learning recently and are proving to be valuable tools. At their core, multiscale methods capture the local geometry of neighborhoods defined by a series of distances between points or sets of nearest neighbors. This is a bit like viewing a part of a slide through a series of microscope resolutions. At high resolutions, very small features are captured in a small space within the sample. At lower resolutions, more of the slide is visible, and a person can investigate bigger features.Main advantages of multiscale methods include improved performance relative to state-of-the-art methods and dramatic reductions in necessary sample size to achieve these results.

As a simple example, consider taking the mean of nearest neighbors within a number line or two-dimensional space. When k increases, the mean of point sets on the number line becomes more spread out, with farther neighbors pulling the mean more than nearer neighbors. Nearest neighbors that are farther away from an existing set of points tend to drag the mean further than added points that are closer to the existing set of points. In the number line example, say the points sit at 1, 2, 4, 5, 9, 11, and 14. Consider the set of the left most point (at 1) and its 3 nearest neighbors: 2, 4, and 5. The mean for this set is 3, which has 2 points with higher values and 2 points with lower values. When 9 is added to the set as a 4^th nearest neighbor of point 1, the mean jumps to 4.2, which is skewed towards point 9 rather than the 4 points whose values are close to one another. Examining the mean of point 1’s 3 nearest neighbors reveals a set of points with fairly similar values and variance among values. However, examining the 4 nearest neighbors of point 1 captures the presence of an outlier. The KNN mean function with a single value of k fails to capture some of these important local properties that emerge at different scales, and important information is lost.

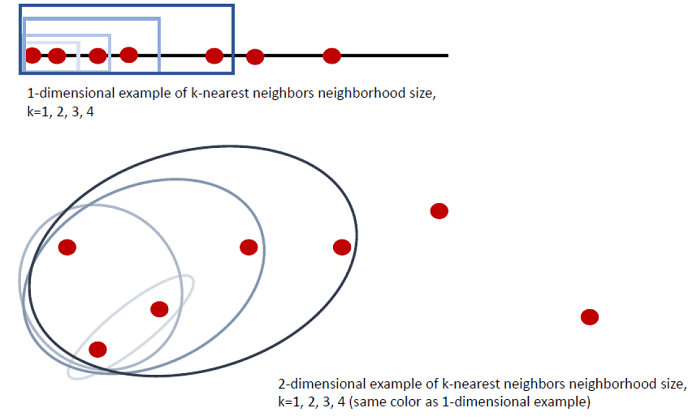
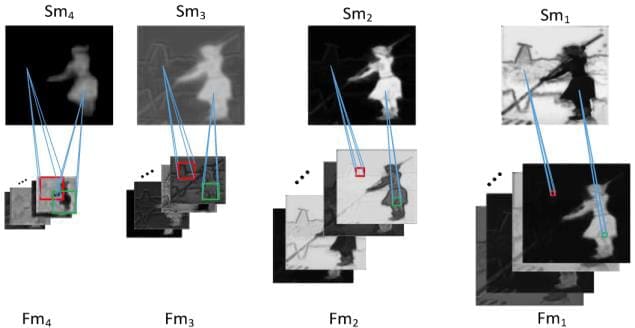
Not all multiscale methods rely on KNN-defined scales, but they do employ similar principles that allow the method to learn multiscale features within a dataset. Grouping points within a series of distances, providing a series of convolutions of different scales, and employing hierarchies of clusters are common choices in multiscale methods. A recent deep learning paper by Pelt & Sethian (2017) based on multiscale methods was able to learn image segmentation and image classification on training sets as small as 6 images with high accuracy (>90%); this algorithm significantly reduced tuning requirements of the deep learning framework, as well. Another deep learning paper (Xiao et al., 2018) blends global image characteristics with a series of local extractions (in convolution layers, shown below) to capture many different scales of image features within a single deep learning framework. This algorithm consistently outperformed state-of-the-art deep learning algorithms on several benchmark datasets, suggesting that multiscale methods can improve even state-of-the-art convolution networks.

Recent work on k-nearest neighbor (KNN) regression and classification ensembles using varied neighborhood size have shown dramatic improvement over not only the KNN algorithms with a single value for k but also other machine learning methods. The multiscale tools of topological data analysis (TDA), including persistent homology, have aided analysis of small datasets, images, videos, and other types of data, providing data scientists and machine learning researchers with a robust, general unsupervised learning tool. A recently-added multiscale component on the TDA tool Mapper improved theoretical stability of the algorithm and yielded consistent results.

Alternatives to multiscale methods exist, but they often come with a cost. Rather than improve performance and compute times with a small training sample, many provide either improved performance or reduction in necessary sample size. Bayesian methods, the main competitor of multiscale methods in recent years, have reduced the necessary sample size for good performance of deep learning algorithms, but they come with a high computational cost that may not be appealing for online algorithm use or quick turnaround of analyses in industry. These methods also require a high degree of statistical expertise that many practitioners may not have. Deep learning has become a ubiquitous, general tool in recent years, but its power seems to lie in the asymptotic properties. Rather than level-off in performance when a large enough sample size is reached for the algorithm to converge, deep learning algorithms continue to improve with further increases in sample size. This is desirable when a lot of data is available, but many industry use cases and research problems involve small datasets or limited examples for a given class.

It seems that local geometry matters. What is relevant and important for one neighborhood may not be relevant or important for a larger neighborhood surrounding the original one, and examining multiple scales can help capture all the important features, rather than the neighborhood yielding the best subset of features. Given the success of multiscale methods on a variety of learning tasks and their enhancement many types of algorithms, it is likely that machine learning will see more algorithms incorporating multiscale subsets in the coming years.

References

Dey, T. K., Mémoli, F., & Wang, Y. (2016). Multiscale mapper: Topological summarization via codomain covers. In Proceedings of the twenty-seventh annual acm-siam symposium on discrete algorithms (pp. 997-1013). Society for Industrial and Applied Mathematics.

Farrelly, C. M. (2017). KNN Ensembles for Tweedie Regression: The Power of Multiscale Neighborhoods. arXiv preprint arXiv:1708.02122.

Pelt, D. M., & Sethian, J. A. (2017). A mixed-scale dense convolutional neural network for image analysis. Proceedings of the National Academy of Sciences, 201715832.

Xia, K., & Wei, G. W. (2014). Persistent homology analysis of protein structure, flexibility, and folding. International journal for numerical methods in biomedical engineering, 30(8), 814-844.

Xiao, F., Deng, W., Peng, L., Cao, C., Hu, K., &Gao, X. (2018). MSDNN: Multi-Scale Deep Neural Network for Salient Object Detection. arXiv preprint arXiv:1801.04187.

Bio: Colleen M. Farrelly is a data scientist whose industry experience includes positions related to healthcare, education, biotech, marketing, and finance. Her areas of research include topology/topological data analysis, ensemble learning, nonparametric statistics, manifold learning, and explaining mathematics to lay audiences (https://www.quora.com/profile/Colleen-Farrelly-1). When she isn’t doing data science, she is a poet and author (https://www.amazon.com/Colleen-Farrelly/e/B07832WQG7).

Related:

• A Tour of The Top 10 Algorithms for Machine Learning Newbies
• Deep Misconceptions About Deep Learning
• How to do Machine Learning Efficiently