Facebook Uses Bayesian Optimization to Conduct Better Experiments in Machine Learning Models
A research from Facebook proposes a Beyasian optimization method to run A/B tests in machine learning models.
I recently started a new newsletter focus on AI education. TheSequence is a no-BS( meaning no hype, no news etc) AI-focused newsletter that takes 5 minutes to read. The goal is to keep you up to date with machine learning projects, research papers and concepts. Please give it a try by subscribing below:
Hyperparameter optimization is a key aspect of the lifecycle of machine learning applications. While methods such as grid search are incredibly effective for optimizing hyperparameters for specific isolated models, they are very difficult to scale across large permutations of models and experiments. A company like Facebook operates thousands of concurrent machine learning models that need to be constantly tuned. To achieve that, Facebook engineering teams need to regularly conduct A/B tests in order to determine the right hyperparameter configuration. Data in those tests is difficult to collect and they are typically conducted in isolation of each other which end up resulting in very computationally expensive exercises. One of the most innovative approaches in this area came from a team of AI researchers from Facebook who published a paper proposing a method based on Bayesian optimization to adaptively design rounds of A/B tests based on the results of prior tests.
Why Bayesian Optimization?
Bayesian optimization is a powerful method for solving black-box optimization problems that involve expensive function evaluations. Recently, Bayesian optimization has evolved as an important technique for optimizing hyperparameters in machine learning models. Conceptually, Bayesian optimization starts by evaluating a small number of randomly selected function values, and fitting a Gaussian process (GP) regression model to the results. The GP posterior provides an estimate of the function value at each point, as well as the uncertainty in that estimate. The GP works well for Bayesian optimization because it provides excellent uncertainty estimates and is analytically tractable. It provides an estimate of how an online metric varies with the parameters of interest.
Let’s imagine an environment in which we are conducting random and regular experiments on machine learning models. In that scenario, Bayesian optimization can be used to construct a statistical model of the relationship between the parameters and the online outcomes of interest and uses that model to decide which experiments to run. The concept is well illustrated in the following figure in which each data marker corresponds to the outcome of an A/B test of that parameter value. We can use the GP to decide which parameter to test next by balancing exploration (high uncertainty) with exploitation (good model estimate). This is done by computing an acquisition function that estimates the value of running an experiment with any given parameter value.
The fundamental goal of Bayesian optimization when applied to hyperparameter optimization is to determine how valuable is an experiment for a specific hyperparameter configuration. Conceptually, Bayesian optimization works very efficiently for isolated models but its value proposition is challenged when used in scenarios running random experiments. The fundamental challenge is related to the noise introduced in the observations.
Noise and Bayesian Optimization
Random experiments in machine learning systems introduce high levels of noise in the observations. Additionally, many of the constraints for a given experiment can be considered noisy data in and out itself which can affect the results of an experiment. Suppose that we are trying to evaluate the value of a function f(x) for a given observation x. With observation noise, we now have uncertainty not only in the value f(x), but we also have uncertainty in which observation is the current best, x*, and its value, f(x*).
Typically, Bayesian optimization models use heuristics to handle noisy observations but those perform very poorly with high levels of noise. To address this challenge, the Facebook team came up with a clever answer: why not to factor in noise as part of the observations?
Imagine if, instead of computing the expectation of observing f(x) we observe yi = f(xi) + €i, where €i is the observation noise. Mathematically, GP works similarly with noise observation as it does with noiseless data. Without going crazy about the math, in their research paper, the Facebook team showed that this type of approximation is very well suited for Monte Carlo optimizations which yield incredibly accurate results estimating the correct observation.
Bayesian Optimization with Noisy Data in Action
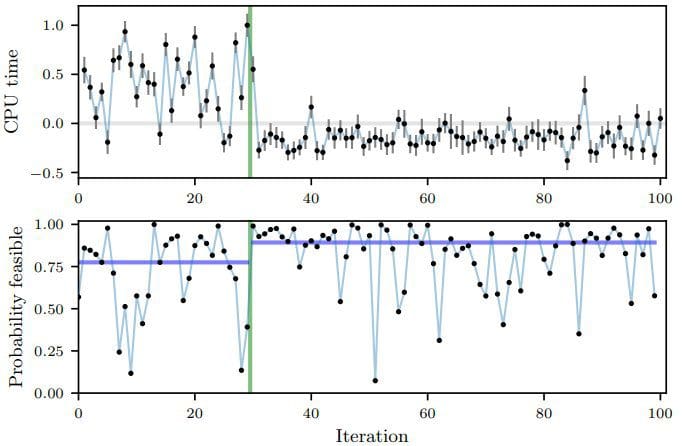
The Facebook team tested their research in a couple of real world scenarios at Facebook scale. The first was to optimize 6 parameters of one of Facebook’s ranking systems. The second example was to optimize 7 numeric compiler flags related to CPU usage used in their HipHop Virtual Machine(HHVM). For that second experiment, the first 30 iterations were randomly created. At that point, the Bayesian optimization with noisy data method was able to identity CPU time as the hyperparameter configuration that needed to be evaluated and started running different experiments to optimize its value. The results are clearly illustrated in the following figure.
Techniques such as Bayesian optimization with noisy data are incredibly powerful in large scale machine learning algorithms. While we have done a lot of work on optimization methods, most of those methods remain highly theoretical. Its nice to see Facebook pushing the boundaries of this nascent space.
Original. Reposted with permission.
Related:
- Essential Resources to Learn Bayesian Statistics
- Uber’s Ludwig is an Open Source Framework for Low-Code Machine Learning
- Facebook Open Sources Blender, the Largest-Ever Open Domain Chatbot