Key Data Science Algorithms Explained: From k-means to k-medoids clustering

By Arushi Prakash, Applied Scientist at Amazon.

The k-means clustering algorithm is a foundational algorithm that every data scientist should know. It is popular because it is simple, fast, and efficient. It works by dividing all the points into a preselected number (k) of clusters based on the distance between the point and the center of each cluster. The original k-means algorithm is limited because it works only in the Euclidean space and results in suboptimal cluster assignments when the real clusters are unequal in size. Despite its shortcomings, k-means remains one of the most powerful tools for clustering and has been used in healthcare, natural language processing, and physical sciences.

Extensions of the k-means algorithms include smarter starting positions for its k centers, allowing variable cluster sizes, and including more distances than Euclidean distance. In this article, we will focus on methods like PAM, CLARA, and CLARANS, which incorporate distance measures beyond the Euclidean distance. These methods are yet to enjoy the fame of k-means because they are slower than k-means for large datasets without a comparable gain in optimality. However, as we will see in this article, researchers have developed newer versions of these algorithms that promise to provide better accuracy and speeds than k-means.

What are the shortcomings of k-means clustering?

For anyone who needs a quick reminder, StatQuest has a great video on k-means clustering.

For this article, we will focus on where k-means fails. Vanilla k-means, as explained in the video, has several disadvantages:

1. It is difficult to predict the correct number of centroids (k) to partition the data.
2. The algorithm always divides the space into k clusters, even when the partitions don’t make sense.
3. The initial positions of the k centroids can affect the results significantly.
4. It does not work well when the expected clusters differ in size and density.
5. Since it is a centroid-based approach, outliers in the data can drag the centroids to inaccurate centers.
6. Since it is a hard clustering method, clusters cannot overlap.
7. It is sensitive to the scale of the dimensions, and rescaling the data can change the results significantly.
8. It uses the Euclidean distance to divide points. The Euclidean distance becomes ineffective in high dimensional spaces since all points tend to become uniformly distant from each other. Read a great explanation here.
9. The centroid is an imaginary point in the dataset and may be meaningless.
10. Categorical variables cannot be defined by a mean and should be described by their mode.

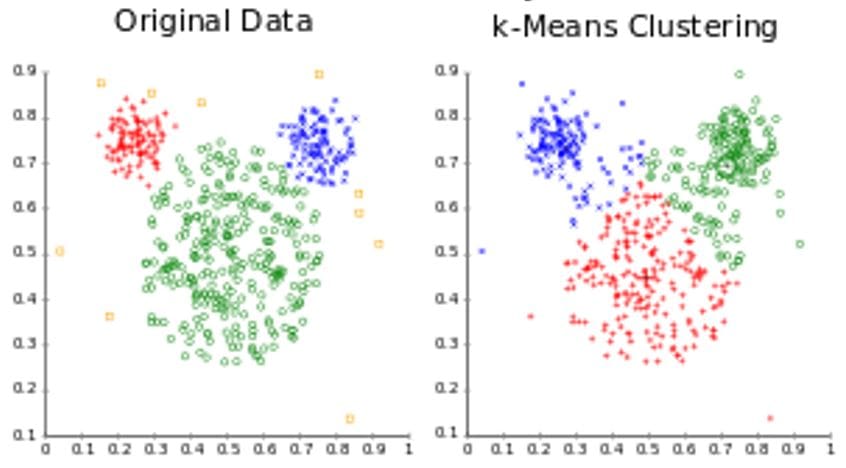
The above figure shows an example of k-means clustering of the mouse data set using k-means, where k-means performs poorly due to varying cluster sizes.

Introducing Partitioning Around Medoids (PAM) algorithm

Instead of using the mean of the cluster to partition, the medoid, or the most centrally located data point in the cluster can be used to partition the data points; The medoid is the least dissimilar point to all points in the cluster. The medoid is also less sensitive to outliers in the data. These partitions can also use arbitrary distances instead of relying on the Euclidean distance. This is the crux of the clustering algorithm named Partition Around Medoids (PAM), and its extensions CLARA and CLARANS. Watch this video for a succinct explanation of the method.

In short, the following are the steps involved in the PAM method (reference):

Improving PAM with sampling

The time complexity of the PAM algorithm is in the order of O(k(n - k)²), which makes it much slower than the k-means algorithm. Kaufman and Rousseeuw (1990) proposed an improvement that traded optimality for speed, named CLARA (Clustering For Large Applications). In CLARA, the main dataset is split into several smaller, randomly sampled subsets of the data. The PAM algorithm is applied to each subset to obtain the medoids for each set, and the set of medoids that give the best performance on the main dataset are kept. Dudoit and Fridlyand (2003) improve the CLARA workflow by combining the medoids from different samples by voting or bagging, which aims to reduce the variability that would come from applying CLARA.

Another variation named CLARANS (Clustering Large Applications based upon RANdomized Search) (Ng and Han 2002) works by combining sampling and searching on a graph. In this graph, each node represents a set of k medoids. Each node is connected to another node if the set of k medoids in each node differs by one. The graph can be traversed until a local minimum is reached, and that minimum provides the best estimate for the medoids of the dataset.

Making PAM faster

Schubert and Rousseeuw (2019) proposed a faster version of PAM, which can be extended to CLARA, by changing how the algorithm caches the distance values. They summarize it well here:

“This caching was enabled by changing the nesting order of the loops in the algorithm, showing once more how much seemingly minor-looking implementation details can matter (Kriegel et al., 2017). As a second improvement, we propose to find the best swap for each medoid and execute as many as possible in each iteration, which reduces the number of iterations needed for convergence without loss of quality, as demonstrated in the experiments, and as supported by theoretical considerations. In this article, we proposed a modification of the popular PAM algorithm that typically yields an O(k) fold speedup, by clever caching of partial results in order to avoid recomputation.”

In another variation, Yue et al. (2016) proposed a MapReduce framework for speeding up the calculations of the k-medoids algorithm and named it the K-Medoids++ algorithm.

More recently, Tiwari et al. (2020) cast the problem of choosing k medoids into a multi-arm bandit problem and solved it using the Upper Confidence Bound algorithm. This variation was faster than PAM and matched its accuracy.

Conclusion

The k-means clustering algorithm has several drawbacks, such as reliance on Euclidean distance, susceptibility to outliers, and obtaining centroids that are not representative of real data points. These are resolved using PAM and its variations. However, PAM is harder to implement and runs slower than the k-means method. This has prompted researchers to develop methods like CLARA, and CLARANS, which increases the speed of clustering at the cost of optimal assignment of clusters. Among new developments in PAM-based clustering, banditPAM, sounds promising as it improves runtime without sacrificing accuracy.

Bio: Arushi Prakash, Ph.D. is a data scientist with experience in the retail industry who is passionate about building better data products and data science education.

Related:

• Centroid Initialization Methods for k-means Clustering
• Understanding Density-based Clustering
• Machine Learning in Power BI using PyCaret