Implementing the AdaBoost Algorithm From Scratch

By James Ajeeth J, Praxis Business School

 
At the end of this article, you will be able to:

• Understand the working and math behind Adaptive Boosting (AdaBoost) Algorithm.
• Able to write the AdaBoost python code from scratch.

 

Introduction to Boosting:

 
Boosting is an ensemble technique that attempts to create strong classifiers from a number of weak classifiers. Unlike many machine learning models which focus on high quality prediction done using single model, boosting algorithms seek to improve the prediction power by training a sequence of weak models, each compensating the weaknesses of its predecessors. Boosting grants power to machine learning models to improve their accuracy of prediction.

 

AdaBoost:

 
AdaBoost, short for Adaptive Boosting, is a machine learning algorithm formulated by Yoav Freund and Robert Schapire. AdaBoost technique follows a decision tree model with a depth equal to one. AdaBoost is nothing but the forest of stumps rather than trees. AdaBoost works by putting more weight on difficult to classify instances and less on those already handled well. AdaBoost algorithm is developed to solve both classification and regression problem.

Idea behind AdaBoost:

• Stumps (one node and two leaves) are not great in making accurate classification so it is nothing but a week classifier/ weak learner. Combination of many weak classifier makes a strong classifier and this is the principle behind the AdaBoost algorithm.
• Some stumps get more performance or classify better than others.
• Consecutive stump is made by taking the previous stumps mistakes into account.

 

AdaBoost Algorithm from scratch:

 
Here I have used Iris dataset as an example in building the algorithm from scratch and also considered only two classes (Versicolor and Virginica) for better understanding.

 

 

Step 1: Assign Equal Weights to all the observations

 
Initially assign same weights to each record in the dataset.

Sample weight = 1/N

Where N = Number of records

 

 

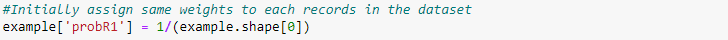
Step 2: Classify random samples using stumps

 
Draw random samples with replacement from original data with the probabilities equal to the sample weights and fit the model. Here the model (base learners) used in AdaBoost is decision tree. Decision trees are created with one depth which has one node and two leaves also referred to as stumps. Fit the model to the random samples and predict the classes for the original data.

 

 

 

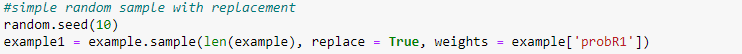
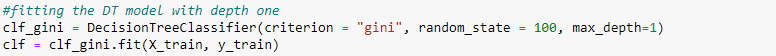
‘pred1’ is the newly predicted class.

 

Step 3: Calculate Total Error

 
Total error is nothing but the sum of weights of misclassified record.

Total Error = Weights of misclassified records

Total error will be always between 0 and 1.

0 represents perfect stump (correct classification)

1 represents weak stump (misclassification)

 

 

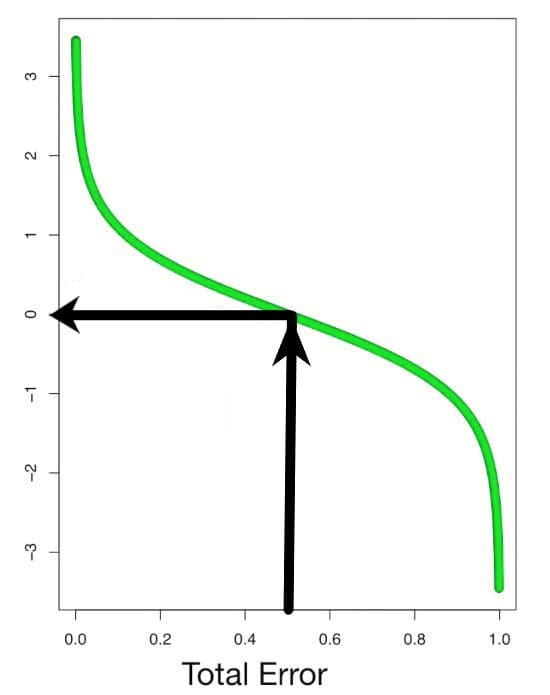
Step 4: Calculate Performance of the Stump

 
Using the Total Error, determine the performance of the base learner. The calculated performance of stump(α) value is used to update the weights in consecutive iteration and also used for final prediction calculation.

Performance of the stump(α) = ½ ln (1 – Total error/Total error)

 

 

Cases:

• If the total error is 0.5, then the performance of the stump will be zero.
• If the total error is 0 or 1, then the performance will become infinity or -infinity respectively.

When the total errors are equal to 1 or 0, the above equation will behave in a weird manner. So, in practice a small error term is added to prevent this from happening.

When the performance(α) is relatively large, the stump did a good job in classifying the records. When the performance(α) is relatively low, the stump did not do a good job in classifying the records. Using the performance parameter(α), we can increase the weights of the wrongly classified records and decrease the weights of the correctly classified records.

 

Step 5: Update Weights

 
Based on the performance of the stump(α) update the weights. We need the next stump to correctly classify the misclassified record by increasing the corresponding sample weight and decreasing the sample weights of the correctly classified records.

New weight = Weight * e^{(performance)} → misclassified records

New weight = Weight * e^{-(performance)} → correctly classified records

 

If the ‘Label’ and ‘pred1’ are same (i.e. 1 or -1) then substituting the values in the above equation will give the equation corresponding to correctly classified record. Similarly, if the values are different then substituting the values in the above equation will give the equation corresponding to misclassified record.

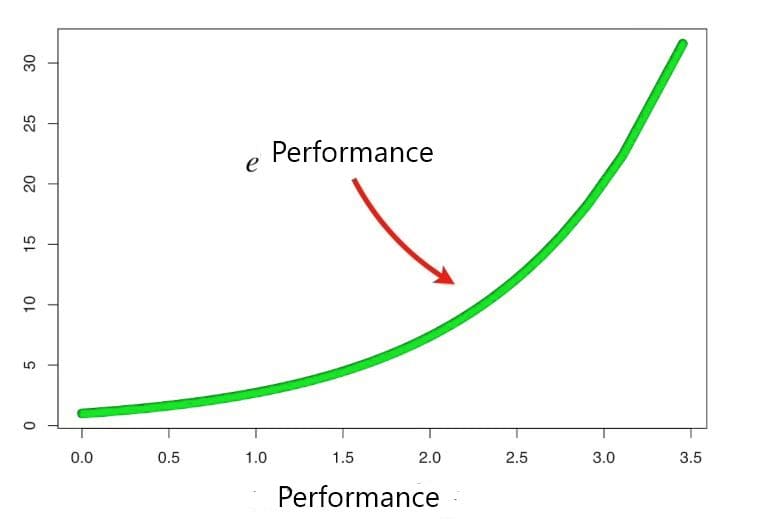
Short note on e^(performance) i.e. for misclassification

When the performance is relatively large the last stump did a good job in classifying the records now the new sample weight will be much larger than the old one. When the performance is relatively low the last stump did not do a good job in classifying the records now the new sample weight will only be little larger than the old one.

 

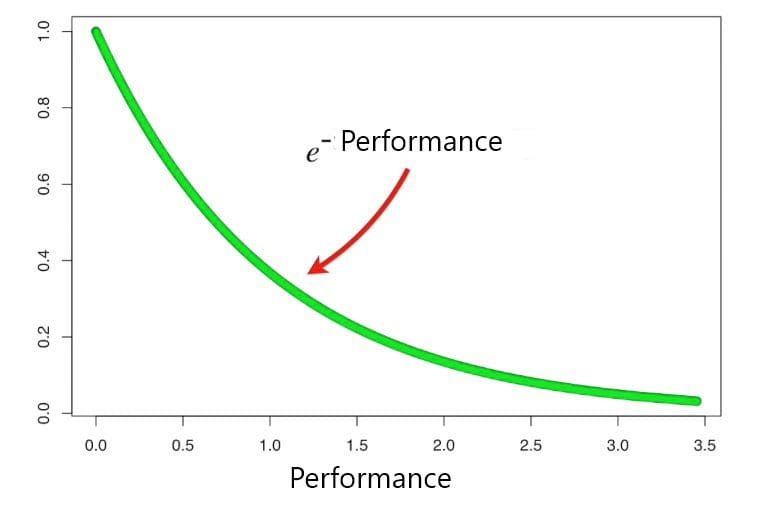
Short note on e^-(performance) i.e. for no misclassification

When the performance is relatively large the last stump did a good job in classifying the records now the new sample weight will be very small than the old one. When the performance is relatively small the last stump did not do a good job in classifying the records now the new sample weight will only be little smaller than the old one.

 

Here the sum of the updated weights is not equal to 1. whereas in case of initial sample weight the sum of total weights is equal to 1. So, to achieve this we will be dividing it by a number which is nothing but the sum of the updated weights (normalizing constant).

Normalizing constant = ∑ New weight

Normalized weight = New weight / Normalizing constant

Now the sum of normalized weight is equal to 1.

 

 

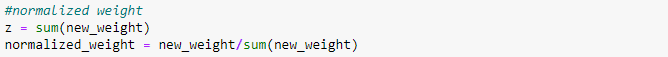
‘prob2’ is the newly updated weights.

 

Step 6: Update weights in iteration

 
Use the normalized weight and make the second stump in the forest. Create a new dataset of same size of the original dataset with repetition based on the newly updated sample weight. So that the misclassified records get higher probability of getting selected. Repeat step 2 to 5 again by updating the weights for a particular number of iterations.

 

‘prob4’ is the final weights of each observation.

 

Step 7: Final Predictions

 
Final prediction is done by obtaining the sign of the weighted sum of final predicted value.

Final prediction/sign (weighted sum) = ∑ (α_i* (predicted value at each iteration))

For example: 5 weak classifiers may predict the values 1.0, 1.0, -1.0, 1.0, -1.0. From a majority vote, it looks like the model will predict a value of 1.0 or the first class. These same 5 weak classifiers may have the performance (α) values as 0.2, 0.5, 0.8, 0.2 and 0.9 respectively. Calculating the weighted sum of these predictions results in an output of -0.8, which would be an ensemble prediction of -1.0 or the second class.

Calculation:

t = 1.0*0.2 + 1.0*0.5 - 1.0*0.8 + 1.0*0.2 - 1.0*0.9 = -0.8

Taking the sign alone into consideration, the final prediction will be -1.0 or the second class.

 

Advantages of AdaBoost Algorithm:

• One of the many advantages of the AdaBoost Algorithm is it is fast, simple and easy to program.
• Boosting has been shown to be robust to overfitting.
• It has been extended to learning problems beyond binary classification (i.e.) it can be used with text or numeric data.

Drawbacks:

• AdaBoost can be sensitive to noisy data and outliers.
• Weak classifiers being too weak can lead to low margins and overfitting.

 

Conclusion:

 
AdaBoost helps in choosing the training set for each new classifier that is trained based on the results of the previous classifier. Also, while combining the results; it determines how much weight should be given to each classifier’s proposed answer. It combines the weak learners to create a strong one to correct classification errors which is also the first successful boosting algorithm for binary classification problems.

GitHub Link for the code file and data:

https://github.com/jamesajeeth/Data-Science/tree/master/Adaboost%20from%20scratch

 
References:

Book:

• Hastie, Trevor, Tibshirani, Robert, Friedman, Jerome, The Elements of Statistical Learning, Data Mining, Inference, and Prediction, Second Edition.

Sites:

• Brief about Adaboost Algorithm
• Statquest
• Wikipedia

 
Bio: James Ajeeth J is a Postgraduate Student at Praxis Business School in Bangalore, India.

Related:

• Ensemble Methods for Machine Learning: AdaBoost
• Exploring The Brute Force K-Nearest Neighbors Algorithm
• Most Popular Distance Metrics Used in KNN and When to Use Them