Beyond the Nash Equilibrium: DeepMind Clever Strategy to Solve Asymmetric Games
The method expands the concept of a Nash equilibrium by decomposing an asymmetric game into multiple symmetric games.
I recently started a new newsletter focus on AI education and already has over 50,000 subscribers. TheSequence is a no-BS( meaning no hype, no news etc) AI-focused newsletter that takes 5 minutes to read. The goal is to keep you up to date with machine learning projects, research papers and concepts. Please give it a try by subscribing below:
Game theory is an increasingly important aspect of multi-agent machine learning systems. In recent years, machine learning labs have made many interesting contributions to the field of game theory. Today, I would like to bring your attention to a new method that was recently published by Alphabet’s subsidiary DeepMind and that provides a unique way to tackle asymmetric game problems. DeepMind’s breakthrough can have profound implications in modern multi-agent, AI systems that are often modeled as asymmetric games. Before getting there, let’s try to understand what’s so difficult about asymmetric game environments.
Symmetric vs. Asymmetric Games
Symmetric games are the favorite examples used to illustrate the dynamics of game theory as they are mathematically elegant and near perfect. As we explained before, a symmetric game describes a dynamic in which the different players share the same strategy and goals. Typically, the simplicity of symmetric games makes it easier to model from a computational standpoint. Unfortunately, most real life game environments lack the mathematical elegance of symmetric games.
Asymmetric games describe multi-agent environments in which players have different and often conflicting goals and strategies. Let’s take yesterday’s market collapse as an example. In that environment, some traders were desperately trying to offload their positions while others were trying to accumulate new positions planning for a potential bounce back of the market (doesn’t seem is going to happen today based on the futures ;)). Multiply that strategy for the millions of traders and investors around the world and you have an incredibly chaotic asymmetric game.
In game theory, the solution to many asymmetric game environments is modeled using the Nash equilibrium. The model was named after John Forbes Nash, the American mathematician immortalized by Russell Crow in the movie “A Beautiful Mind”. Essentially, a Nash equilibrium describes a situation in which each player has chosen a strategy and no player can benefit by changing strategies while the other players keep theirs unchanged.
Where The Nash Equilibrium Fails
The Nash equilibrium is a beautiful and incredibly powerful mathematical model to tackle many game theory problems but it also falls short in many asymmetric game environments. Two main reasons:
- For starters, the Nash method assumes that players have infinite computing power which is rarely the case in real world environments.
- Also many Nash equilibrium models fail to account for the notion of risk which is omnipresent in most asymmetric games the economic markets.
As a result, there are many asymmetric game scenarios that are hard to implement using the Nash equilibrium. This is particularly important in multi-agent AI systems that need to find the right balance between the mathematical elegance of the solution and the practicality of its implementation.
DeepMind’s Symmetric Decomposition of Asymmetric Games
In a paper published two years ago by DeepMind, the authors proposed a very clever model to find solutions for highly complex asymmetric games by decomposing them into different symmetric games. In mathematical terms, the new techniques proposes that
if (x,y) is a Nash equilibrium of an asymmetric game (A,B), this implies that y is a Nash equilibrium of the symmetric counterpart game determined by payoff table A, and x is a Nash equilibrium of the symmetric counterpart game determined by payoff table B.
To illustrate the new technique, I am going to borrow an example from the original post in the DeepMind’s website. The example is based on the famous “Battle of the Sexes” game.
Here, two players have to coordinate a night out to either the opera or the movies. One of the players has a slight preference for the opera and one of them has a slight preference for the movies. The game is asymmetric because, while both players have access to the same options, the corresponding rewards for each are different based on the players preferences. In order to maintain their friendship — or equilibrium — the players should choose the same activity (hence the zero payoff for separate activities).
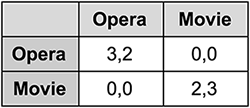
This game has three equilibria:
- both players deciding to go to the opera
- both deciding to go to the movies
- a final, mixed option, where each player will opt for their preferred option three fifths of the time.
The last option, which is said to be “unstable”, can be rapidly uncovered using DeepMind’s new method by simplifying — or decomposing — the asymmetric game into its symmetric counterparts. These counterpart games essentially considers the reward table of each player as a separate symmetric 2-player game with equilibrium points that coincide with the original asymmetric game.
Original. Reposted with permission.
Related:
- A Crash Course in Game Theory for Machine Learning: Classic and New Ideas
- Facebook Open Sourced New Frameworks to Advance Deep Learning Research
- Six Times Bigger than GPT-3: Inside Google’s TRILLION Parameter Switch Transformer Model