Calculus for Data Science
In this article, we discuss the importance of calculus in data science and machine learning.
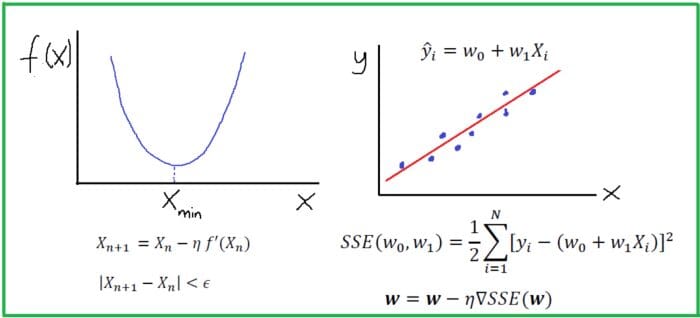
Image by Author
Key Takeaways
- Most beginners interested in getting into the field of data science are always concerned about the math requirements.
- Data science is a very quantitative field that requires advanced mathematics.
- But to get started, you only need to master a few math topics.
- In this article, we discuss the importance of calculus in data science and machine learning.
Calculus in Data Science and Machine Learning
A machine learning algorithm (such as classification, clustering or regression) uses a training dataset to determine weight factors that can be applied to unseen data for predictive purposes. Behind every machine learning model is an optimization algorithm that relies heavily on calculus. In this article, we discuss one such optimization algorithm, namely, the Gradient Descent Approximation (GDA) and we’ll show how it can be used to build a simple linear regression estimator.
Optimization Using the Gradient Descent Algorithm
Derivatives and Gradients
In one-dimension, we can find the maximum and minimum of a function using derivatives. Let us consider a simple quadratic function f(x) as shown below.
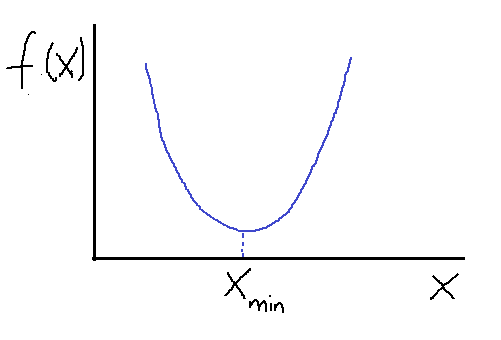
Figure 1. Minimum of a simple function using gradient descent algorithm. Image by Author.
Suppose we want to find the minimum of the function f(x). Using the gradient descent method with some initial guess, X gets updated according to this equation:
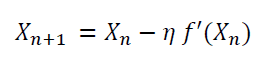
where the constant eta is a small positive constant called the learning rate. Note the following:
- when X_n > X_min, f’(X_n) > 0: this ensures that X_n+1 is less than X_n. Hence, we are taking steps in the left direction to get to the minimum.
- when X_n < X_min, f’(X_n) < 0: this ensures that X_n+1 is greater than X_n. Hence, we are taking steps in the right direction to get to X_min.
The above observation shows that it doesn’t matter what the initial guess is, the gradient descent algorithm will always find the minimum. How many optimization steps it’s going to take to get to X_min depends on how good the initial guess is. Sometimes if the initial guess or the learning rate is not carefully chosen, the algorithm can completely miss the minimum. This is often referred to as an “overshoot”. Generally, one could ensure convergence by adding a convergence criterion such as:
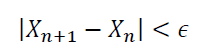
where epsilon is a small positive number.
In higher dimensions, a function of several variables can be optimized (minimized) using the gradient descent algorithm as well. In this case, we use the gradient to update the vector X:
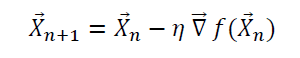
As in one-dimension, one could ensure convergence by adding a convergence criterion such as:
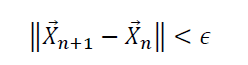
Case Study: Building a Simple Regression Estimator
In this case study, we build a simple linear regression estimator using the gradient descent approximation. The estimator is used to predict house prices using the Housing dataset. Hyperparameter tuning is used to find the regression model with the best performance by evaluating the R2 score (measure of goodness of fit) for different learning rates. The dataset and code for this tutorial can be downloaded from this GitHub repository: https://github.com/bot13956/python-linear-regression-estimator
Summary
- A machine learning algorithm (such as classification, clustering or regression) uses a training dataset to determine weight factors that can be applied to unseen data for predictive purposes.
- Behind every machine learning model is an optimization algorithm that relies heavily on calculus.
- It is therefore important to have fundamental knowledge in calculus as this would enable a data science practitioner to have some understanding of the optimization algorithms used in data science and machine learning.
Benjamin O. Tayo is a Physicist, Data Science Educator, and Writer, as well as the Owner of DataScienceHub. Previously, Benjamin was teaching Engineering and Physics at U. of Central Oklahoma, Grand Canyon U., and Pittsburgh State U.
