Vector and Matrix Norms with NumPy Linalg Norm
Looking to further your Python linear algebra skills? Learn how to compute vector and matrix norms using NumPy’s linalg module.
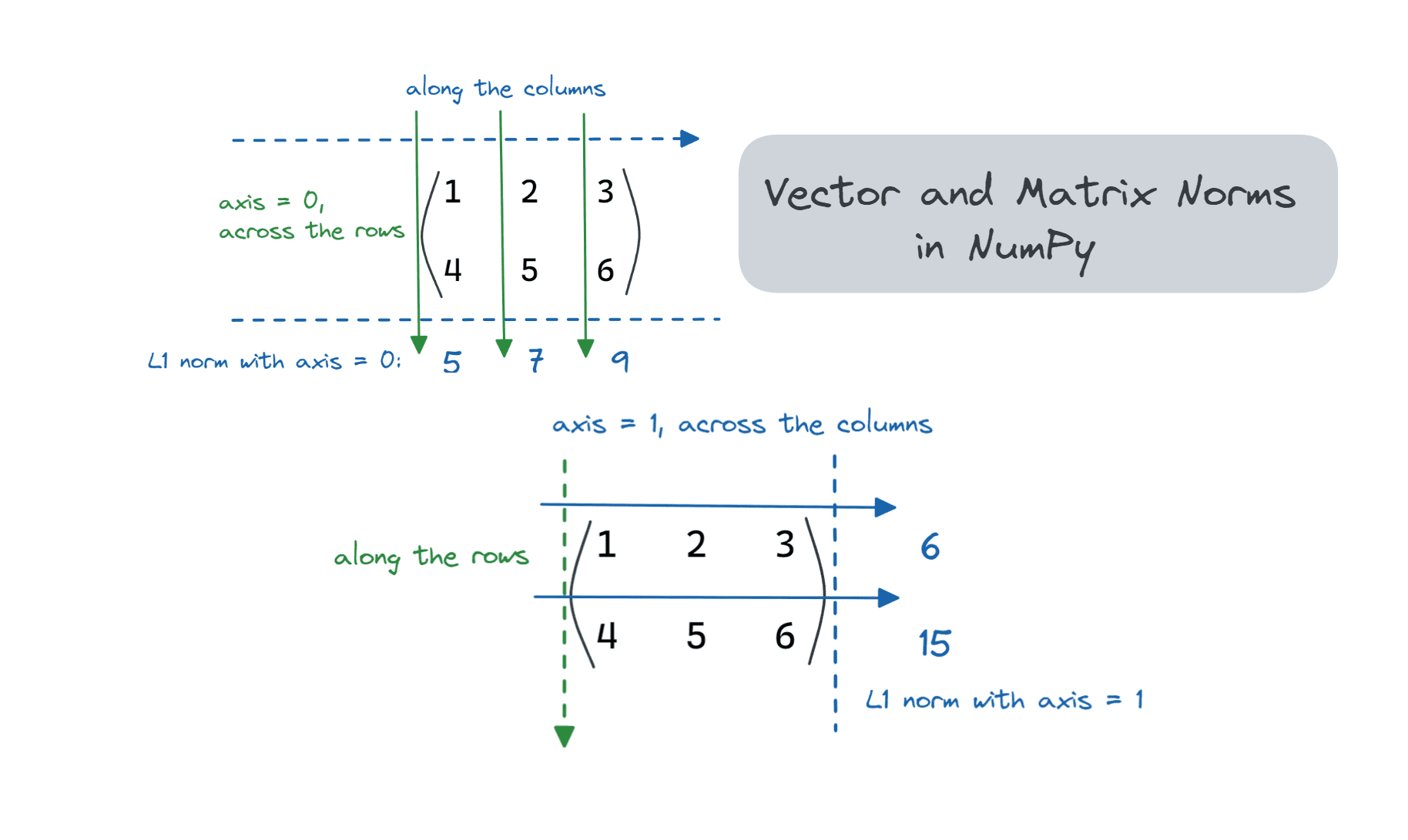
Image by Author
Numerical Python or NumPy is a popular library for scientific computing in Python. The NumPy library has a huge collection of built-in functionality to create n-dimensional arrays and perform computations on them.
If you’re interested in data science, computational linear algebra and related fields, learning how to compute vector and matrix norms can be helpful. And this tutorial will teach you how to do that using functions from NumPy’s linalg module.
To code along, you should have Python and NumPy installed in your development environment. For the f-strings in the print() statements to work without errors, you need to have Python 3.8 or a later version installed.
Let’s begin!
What is a Norm?
In this discussion, we’ll first look at vector norms. We’ll get to matrix norms later. Mathematically, a norm is a function (or a mapping) from an n-dimensional vector space to the set of real numbers:
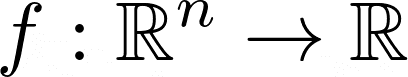
Note: Norms are also defined on complex vector spaces C^n → R is a valid definition of norm, too. But we’ll restrict ourselves to the vector space of real numbers in this discussion.
Properties of Norms
For an n-dimensional vector x = (x1,x2,x3,...,xn), the norm of x, commonly denoted by ||x||, should satisfy the following properties:
- ||x|| is a non-negative quantity. For a vector x, the norm ||x|| is always greater than or equal to zero. And ||x|| is equal to zero if and only if the vector x is the vector of all zeros.
- For two vectors x = (x1,x2,x3,...,xn) and y = (y1,y2,y3,...,yn), their norms ||x|| and ||y|| should satisfy the triangle inequality: ||x + y|| <= ||x|| + ||y||.
- In addition, all norms satisfy ||αx|| = |α| ||x|| for a scalar α.
Common Vector Norms: L1, L2, and L∞ Norms
In general, the Lp norm (or p-norm) of an n-dimensional vector x = (x1,x2,x3,...,xn) for p >= 0 is given by:

Let’s take a look at the common vector norms, namely, the L1, L2 and L∞ norms.
L1 Norm
The L1 norm is equal to the sum of the absolute values of elements in the vector:

L2 Norm
Substituting p =2 in the general Lp norm equation, we get the following expression for the L2 norm of a vector:

L∞ norm
For a given vector x, the L∞ norm is the maximum of the absolute values of the elements of x:
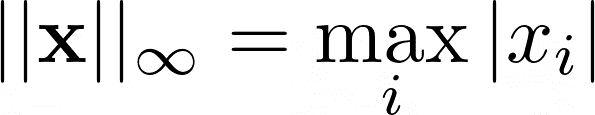
It’s fairly straightforward to verify that all of these norms satisfy the properties of norms listed earlier.
How to Compute Vector Norms in NumPy
The linalg module in NumPy has functions that we can use to compute norms.
Before we begin, let’s initialize a vector:
import numpy as np
vector = np.arange(1,7)
print(vector)
Output >> [1 2 3 4 5 6]
L2 Norm in NumPy
Let’s import the linalg module from NumPy:
from numpy import linalg
The norm() function to compute both matrix and vector norms. This function takes in a required parameter – the vector or matrix for which we need to compute the norm. In addition, it takes in the following optional parameters:
ordthat decides the order of the norm computed, andaxisthat specifies the axis along which the norm is to be computed.
When we don’t specify the ord in the function call, the norm() function computes the L2 norm by default:
l2_norm = linalg.norm(vector)
print(f"{l2_norm = :.2f}")
Output >> l2_norm = 9.54
We can verify this by explicitly setting ord to 2:
l2_norm = linalg.norm(vector, ord=2)
print(f"{l2_norm = :.2f}")
Output >> l2_norm = 9.54
L1 Norm in NumPy
To calculate the L1 norm of the vector, call the norm() function with ord = 1:
l1_norm = linalg.norm(vector, ord=1)
print(f"{l1_norm = :.2f}")
Output >> l1_norm = 21.00
As our examples vector contains only positive numbers, we can verify that L1 norm in this case is equal to the sum of the elements:
assert sum(vector) == l1_norm
L∞ Norm in NumPy
To compute the L∞ norm, set ord to 'np.inf':
inf_norm = linalg.norm(vector, ord=np.inf)
print(f"{inf_norm = }")
In this example, we get 6, the maximum element (in the absolute sense) in the vector:
Output >> inf_norm = 6.0
In the norm() function, you can also set ord to '-np.inf'.
neg_inf_norm = linalg.norm(vector, ord=-np.inf)
print(f"{neg_inf_norm = }")
As you may have guessed, negative L∞ norm returns the minimum element (in the absolute sense) in the vector:
Output >> neg_inf_norm = 1.0
A Note on L0 Norm
The L0 norm gives the number of non-zero elements in the vector. Technically, it is not a norm. Rather it’s a pseudo norm given that it violates the property ||αx|| = |α| ||x||. This is because the number of non-zero elements remains the same even if the vector is multiplied by a scalar.
To get the number of non-zero elements in a vector, set ord to 0:
another_vector = np.array([1,2,0,5,0])
l0_norm = linalg.norm(another_vector,ord=0)
print(f"{l0_norm = }")
Here, another_vector has 3 non-zero elements:
Output >> l0_norm = 3.0
Understanding Matrix Norms
So far we have seen how to compute vector norms. Just the way you can think of vector norms as mappings from an n-dimensional vector space onto the set of real numbers, matrix norms are a mapping from an m x n matrix space to the set of real numbers. Mathematically, you can represent this as:

Common matrix norms include the Frobenius and nuclear norms.
Frobenius Norm
For an m x n matrix A with m rows and n columns, the Frobenius norm is given by:
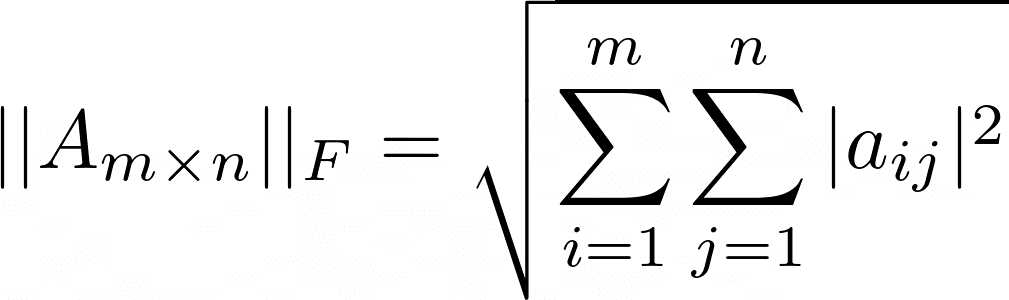
Nuclear Norm
Singular value decomposition or SVD is a matrix factorization technique used in applications such as topic modeling, image compression, and collaborative filtering.
SVD factorizes an input matrix into a matrix of a matrix of left singular vectors (U), a matrix of singular values (S), and a matrix of right singular vectors (V_T). And the nuclear norm is the largest singular value of the matrix.

How to Compute Matrix Norms in NumPy
To continue our discussion on computing matrix norms in NumPy, let’s reshape vector to a 2 x 3 matrix:
matrix = vector.reshape(2,3)
print(matrix)
Output >>
[[1 2 3]
[4 5 6]]
Matrix Frobenius Norm in NumPy
If you do not specify the ord parameter, the norm() function, by default, calculates the Frobenius norm.
Let's verify this by setting ord to 'fro':
frob_norm = linalg.norm(matrix,ord='fro')
print(f"{frob_norm = :.2f}")
Output >> frob_norm = 9.54
When we don’t pass in the optional ord parameter, we get the Frobenius norm, too:
frob_norm = linalg.norm(matrix)
print(f"{frob_norm = :.2f}")
Output >> frob_norm = 9.54
To sum up, when the norm() function is called with a matrix as the input, it returns the Frobenius norm of the matrix by default.
Matrix Nuclear Norm in NumPy
To calculate the nuclear norm of a matrix, you can pass in the matrix and set ord to 'nuc' in the norm() function call:
nuc_norm = linalg.norm(matrix,ord='nuc')
print(f"{nuc_norm = :.2f}")
Output >> nuc_norm = 10.28
Matrix Norms Along a Specific Axis
We generally do not compute L1 and L2 norms on matrices, but NumPy lets you compute norms of any ord on matrices (2D-arrays) and other multi-dimensional arrays.
Let’s see how to compute the L1 norm of a matrix along a specific axis – along the rows and columns.
Similarly, we can set axis = 1.
axis = 0 denotes the rows of a matrix. If you set axis = 0, the L1 norm of the matrix is calculated across the rows (or along the columns), as shown:
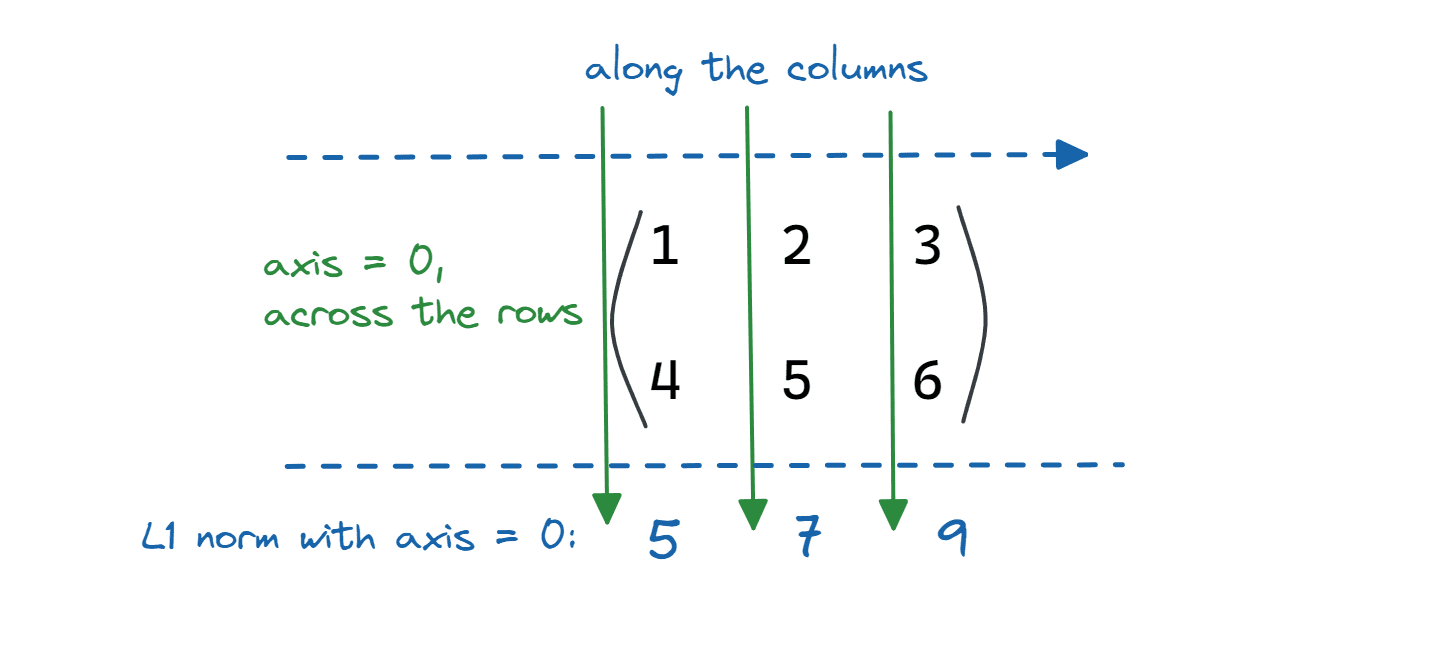
Image by Author
Let’s verify this in NumPy:
matrix_1_norm = linalg.norm(matrix,ord=1,axis=0)
print(f"{matrix_1_norm = }")
Output >> matrix_1_norm = array([5., 7., 9.])
Similarly, we can set axis = 1.
axis = 1 denotes the columns of a matrix. So the computation of the L1 norm of the matrix by setting axis = 1 is across the columns (along the rows).
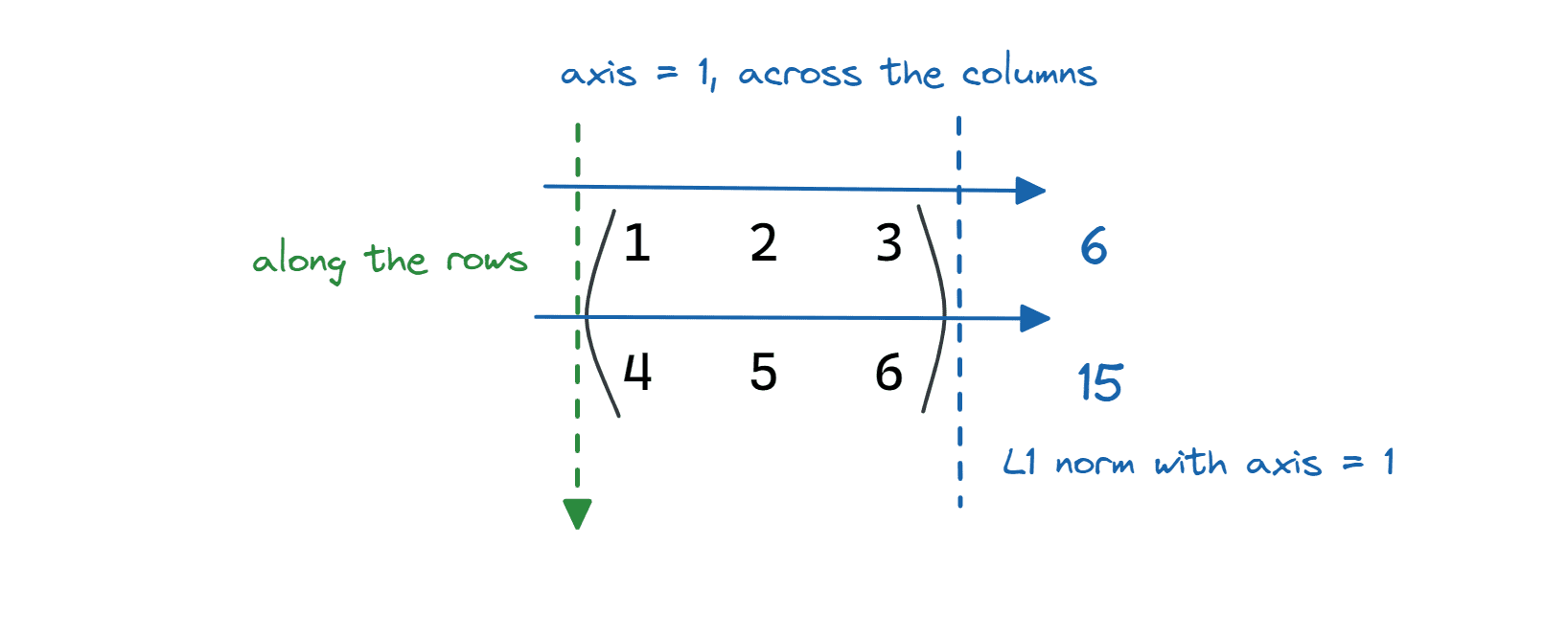
Image by Author
matrix_1_norm = linalg.norm(matrix,ord=1,axis=1)
print(f"{matrix_1_norm = }")
Output >> matrix_1_norm = array([ 6., 15.])
I suggest that you play around with the ord and axis parameters on and try with different matrices until you get the hang of it.
Conclusion
I hope you now understand how to compute vector and matrix norms using NumPy. It’s important, however, to note that the Frobenius and nuclear norms are defined only for matrices. So if you compute for vectors or multidimensional arrays with more than two dimensions, you’ll run into errors. That's all for this tutorial!
Bala Priya C is a technical writer who enjoys creating long-form content. Her areas of interest include math, programming, and data science. She shares her learning with the developer community by authoring tutorials, how-to guides, and more.
