Can noise help separate causation from correlation?
How to tell correlation from causation is one of the key problems in data science and Big Data. New Additive Noise Models methods can do it with over 65% accuracy, opening new breakthrough possibilities.
By Francois Petitjean (@LeDataMiner).
 Correlation isn't causation
Correlation isn't causation
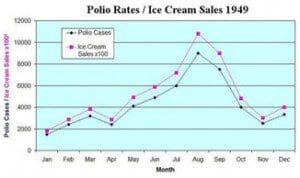
It hasn’t always been well understood that correlation does not imply causation. In the late 1940s for example, public health experts recommended that people stop eating ice cream as part of an anti-polio diet. It turned out however that there was only a correlation between polio incidence and ice-cream consumption, because outbreaks were most common in the summer.
The distinction between correlation and causation is now much better understood. Even if we accept that people who sleep with their shoes on often wake up with a headache, we’d more likely blame both incidents on their having too much to drink the night before than believe that the one is the cause of the other. But what would be the best way to proceed if we did want to determine whether the shoe wearing caused the headache?
Intervention: the gold standard for determining causation
If you can influence A and observe how this modifies B, you might be able to make conclusions as to causation. For example, you can force yourself to go to bed with shoes. Observing that you don’t have more headaches than when you don’t wear shoes, you can tell that the shoes are not causing the headaches.
Most of the time, however, you won't be able to use intervention because:
 Causation from data
Causation from data
So, can we deduce causation from pure observational data? If we’re given data about two variables X and Y, such as the one illustrated on the right, and we know that it’s either X→Y or Y→X (no common ancestor, etc.), can we pick the right direction for the arrow?
Researchers are divided on this question.Some argue that it is simply impossible [1], others, like J. Mooij, are more hopeful and argue that studying the distribution of noise can help us determine the cause and effect [2].
Their intuition is that if X causes Y, then noise affecting X will also affect Y.
 Let me take the example of traffic vs commuting time, borrowed from [3]. When the amount of traffic increases, it takes me more time to commute; when the traffic varies, my commuting time varies also. However, the opposite is less true. Sometimes, it takes me more time to commute than others: I might hit different red lights, be in more or less of a hurry, etc.
Let me take the example of traffic vs commuting time, borrowed from [3]. When the amount of traffic increases, it takes me more time to commute; when the traffic varies, my commuting time varies also. However, the opposite is less true. Sometimes, it takes me more time to commute than others: I might hit different red lights, be in more or less of a hurry, etc.
More precisely, the core idea of these so-called Additive Noise Models (ANM) is that if X→Y, then the variability observed in Y will be either explained by X, or by some noise that is independent of X.
To test if “traffic” affects “commuting time”, they construct the following model:
 This is where it begins to get a tiny bit tricky:
This is where it begins to get a tiny bit tricky:
1. They look at the correlation between traffic and noise (ie the variations of commuting time that are not explained by the traffic).
2. If traffic and noise are independent, it means that the variations of commuting time are independent of the traffic.
3. This leads to being able to state that the noise affecting commuting time does not affect traffic. But, if X → Y is true, we have seen that the noise affecting X should also affect Y (here X is commuting time and Y is traffic).
4. It follows that commuting time is unlikely to cause traffic.
5. We can thus only choose the other direction: traffic → commuting time.
Does this work?
In their paper [2], J. Mooij study the accuracy of these so-called Additive Noise Models (ANM) over 88 datasets and conclude that ANM methods can put the right direction on the arrow with more than 65% accuracy. This opens new possibilities for inferring causation in circumstances where traditional methods make it unethical, impossible, or too expensive to do so.
Bio
My name is Francois Petitjean (@LeDataMiner), and I try to develop useful solutions for big data. I completed my PhD working for the French Space Agency in 2012, and since then have been working in Geoff Webb’s team at Monash University’s Centre for Data Science.More at www.francois-petitjean.com.
References
[1] L. Wasserman. All of Statistics. Springer, New York, 2004.
[2] J. Mooij, J. Peters, D. Janzing, J. Zscheischler and B. Schölkopf, “Distinguishing cause from effect using observational data: methods and benchmarks,” arXiv:1412.3773
[3] Mathematicians have finally figured out how to tell correlation from causation, QZ
Related:
 Correlation isn't causation
Correlation isn't causationIt hasn’t always been well understood that correlation does not imply causation. In the late 1940s for example, public health experts recommended that people stop eating ice cream as part of an anti-polio diet. It turned out however that there was only a correlation between polio incidence and ice-cream consumption, because outbreaks were most common in the summer.
The distinction between correlation and causation is now much better understood. Even if we accept that people who sleep with their shoes on often wake up with a headache, we’d more likely blame both incidents on their having too much to drink the night before than believe that the one is the cause of the other. But what would be the best way to proceed if we did want to determine whether the shoe wearing caused the headache?
Intervention: the gold standard for determining causation
If you can influence A and observe how this modifies B, you might be able to make conclusions as to causation. For example, you can force yourself to go to bed with shoes. Observing that you don’t have more headaches than when you don’t wear shoes, you can tell that the shoes are not causing the headaches.
Most of the time, however, you won't be able to use intervention because:
- it's too expensive (for example if you have to run an experiment with 10,000 patients)
- it's not ethical (for example you can't force people to start smoking)
- it's not possible (for example you can't change the levels of CO2 in the atmosphere)
 Causation from data
Causation from dataSo, can we deduce causation from pure observational data? If we’re given data about two variables X and Y, such as the one illustrated on the right, and we know that it’s either X→Y or Y→X (no common ancestor, etc.), can we pick the right direction for the arrow?
Researchers are divided on this question.Some argue that it is simply impossible [1], others, like J. Mooij, are more hopeful and argue that studying the distribution of noise can help us determine the cause and effect [2].
Their intuition is that if X causes Y, then noise affecting X will also affect Y.
 Let me take the example of traffic vs commuting time, borrowed from [3]. When the amount of traffic increases, it takes me more time to commute; when the traffic varies, my commuting time varies also. However, the opposite is less true. Sometimes, it takes me more time to commute than others: I might hit different red lights, be in more or less of a hurry, etc.
Let me take the example of traffic vs commuting time, borrowed from [3]. When the amount of traffic increases, it takes me more time to commute; when the traffic varies, my commuting time varies also. However, the opposite is less true. Sometimes, it takes me more time to commute than others: I might hit different red lights, be in more or less of a hurry, etc.
More precisely, the core idea of these so-called Additive Noise Models (ANM) is that if X→Y, then the variability observed in Y will be either explained by X, or by some noise that is independent of X.
To test if “traffic” affects “commuting time”, they construct the following model:
commuting time = f(traffic) + noise
They then use a regression to estimate f and noise (ie the residual).
 This is where it begins to get a tiny bit tricky:
This is where it begins to get a tiny bit tricky:1. They look at the correlation between traffic and noise (ie the variations of commuting time that are not explained by the traffic).
2. If traffic and noise are independent, it means that the variations of commuting time are independent of the traffic.
3. This leads to being able to state that the noise affecting commuting time does not affect traffic. But, if X → Y is true, we have seen that the noise affecting X should also affect Y (here X is commuting time and Y is traffic).
4. It follows that commuting time is unlikely to cause traffic.
5. We can thus only choose the other direction: traffic → commuting time.
Does this work?
In their paper [2], J. Mooij study the accuracy of these so-called Additive Noise Models (ANM) over 88 datasets and conclude that ANM methods can put the right direction on the arrow with more than 65% accuracy. This opens new possibilities for inferring causation in circumstances where traditional methods make it unethical, impossible, or too expensive to do so.
Bio
My name is Francois Petitjean (@LeDataMiner), and I try to develop useful solutions for big data. I completed my PhD working for the French Space Agency in 2012, and since then have been working in Geoff Webb’s team at Monash University’s Centre for Data Science.More at www.francois-petitjean.com.
References
[1] L. Wasserman. All of Statistics. Springer, New York, 2004.
[2] J. Mooij, J. Peters, D. Janzing, J. Zscheischler and B. Schölkopf, “Distinguishing cause from effect using observational data: methods and benchmarks,” arXiv:1412.3773
[3] Mathematicians have finally figured out how to tell correlation from causation, QZ
Related:
- Causation vs Correlation: Visualization, Statistics, and Intuition
- Dancing Statistics – who says statistics cannot be fun?
- “Vite fait, bien fait” – Averaging improves both accuracy and speed of time series classification
