The Amazing Power of Word Vectors

For today’s post, I’ve drawn material not just from one paper, but from five! The subject matter is ‘word2vec’ – the work of Mikolov et al. at Google on efficient vector representations of words (and what you can do with them). The papers are:

• Efficient Estimation of Word Representations in Vector Space – Mikolov et al. 2013
• Distributed Representations of Words and Phrases and their Compositionality – Mikolov et al. 2013
• Linguistic Regularities in Continuous Space Word Representations – Mikolov et al. 2013
• word2vec Parameter Learning Explained – Rong 2014
• word2vec Explained: Deriving Mikolov et al’s Negative Sampling Word-Embedding Method – Goldberg and Levy 2014

From the first of these papers (‘Efficient estimation…’) we get a description of theContinuous Bag-of-Words and Continuous Skip-gram models for learning word vectors (we’ll talk about what a word vector is in a moment…). From the second paper we get more illustrations of the power of word vectors, some additional information on optimisations for the skip-gram model (hierarchical softmax and negative sampling), and a discussion of applying word vectors to phrases. The third paper (‘Linguistic Regularities…’) describes vector-oriented reasoning based on word vectors and introduces the famous “King – Man + Woman = Queen” example. The last two papers give a more detailed explanation of some of the very concisely expressed ideas in the Milokov papers.

Check out the word2vec implementation on Google Code.

At one level, it’s simply a vector of weights. In a simple 1-of-N (or ‘one-hot’) encoding every element in the vector is associated with a word in the vocabulary. The encoding of a given word is simply the vector in which the corresponding element is set to one, and all other elements are zero.

Suppose our vocabulary has only five words: King, Queen, Man, Woman, and Child. We could encode the word ‘Queen’ as:

Using such an encoding, there’s no meaningful comparison we can make between word vectors other than equality testing.

In word2vec, a distributed representation of a word is used. Take a vector with several hundred dimensions (say 1000). Each word is representated by a distribution of weights across those elements. So instead of a one-to-one mapping between an element in the vector and a word, the representation of a word is spread across all of the elements in the vector, and each element in the vector contributes to the definition of many words.

If I label the dimensions in a hypothetical word vector (there are no such pre-assigned labels in the algorithm of course), it might look a bit like this:

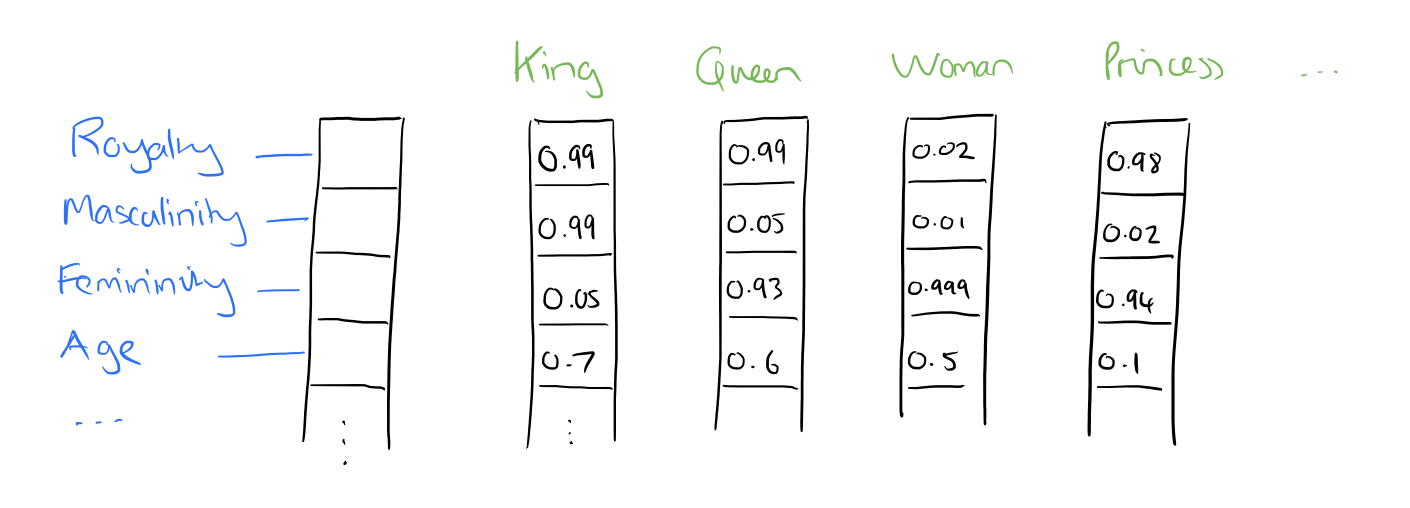
Such a vector comes to represent in some abstract way the ‘meaning’ of a word. And as we’ll see next, simply by examining a large corpus it’s possible to learn word vectors that are able to capture the relationships between words in a surprisingly expressive way. We can also use the vectors as inputs to a neural network.

We find that the learned word representations in fact capture meaningful syntactic and semantic regularities in a very simple way. Specifically, the regularities are observed as constant vector offsets between pairs of words sharing a particular relationship. For example, if we denote the vector for word i as x_i, and focus on the singular/plural relation, we observe that x_apple – x_apples ≈ x_car – x_cars, x_family – x_families ≈ x_car – x_cars, and so on. Perhaps more surprisingly, we find that this is also the case for a variety of semantic relations, as measured by the SemEval 2012 task of measuring relation similarity.

The vectors are very good at answering analogy questions of the form a is to b as cis to ?. For example, man is to woman as uncle is to ? (aunt) using a simple vector offset method based on cosine distance.

For example, here are vector offsets for three word pairs illustrating the gender relation:

And here we see the singular plural relation:

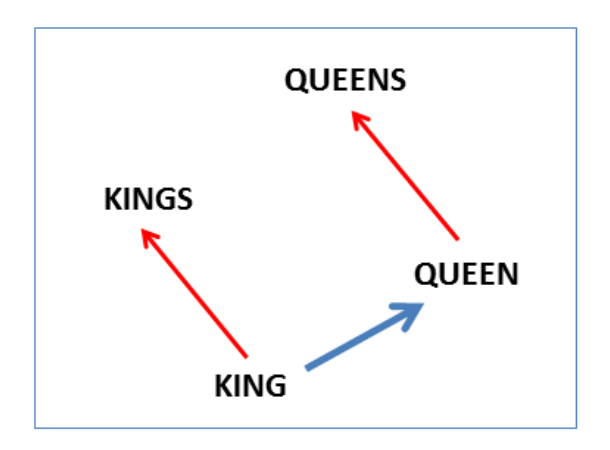
This kind of vector composition also lets us answer “King – Man + Woman = ?” question and arrive at the result “Queen” ! All of which is truly remarkable when you think that all of this knowledge simply comes from looking at lots of word in context (as we’ll see soon) with no other information provided about their semantics.

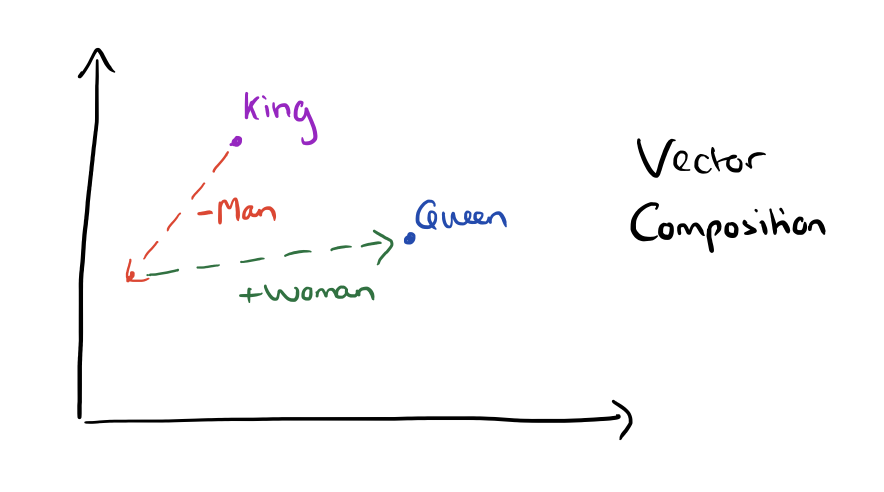
Somewhat surprisingly, it was found that similarity of word representations goes beyond simple syntatic regularities. Using a word offset technique where simple algebraic operations are performed on the word vectors, it was shown for example thatvector(“King”) – vector(“Man”) + vector(“Woman”) results in a vector that is closest to the vector representation of the wordQueen.

Vectors for King, Man, Queen, & Woman:

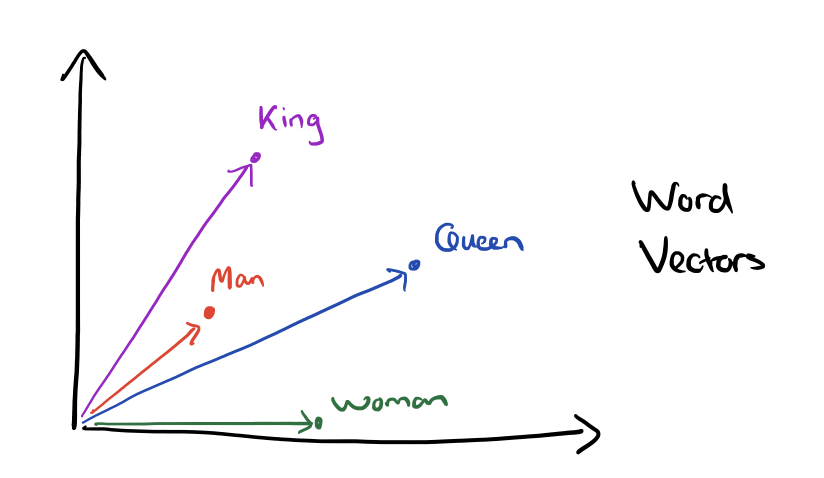
The result of the vector composition King – Man + Woman = ?

Here are some more results achieved using the same technique:

Here’s what the country-capital city relationship looks like in a 2-dimensional PCA projection:

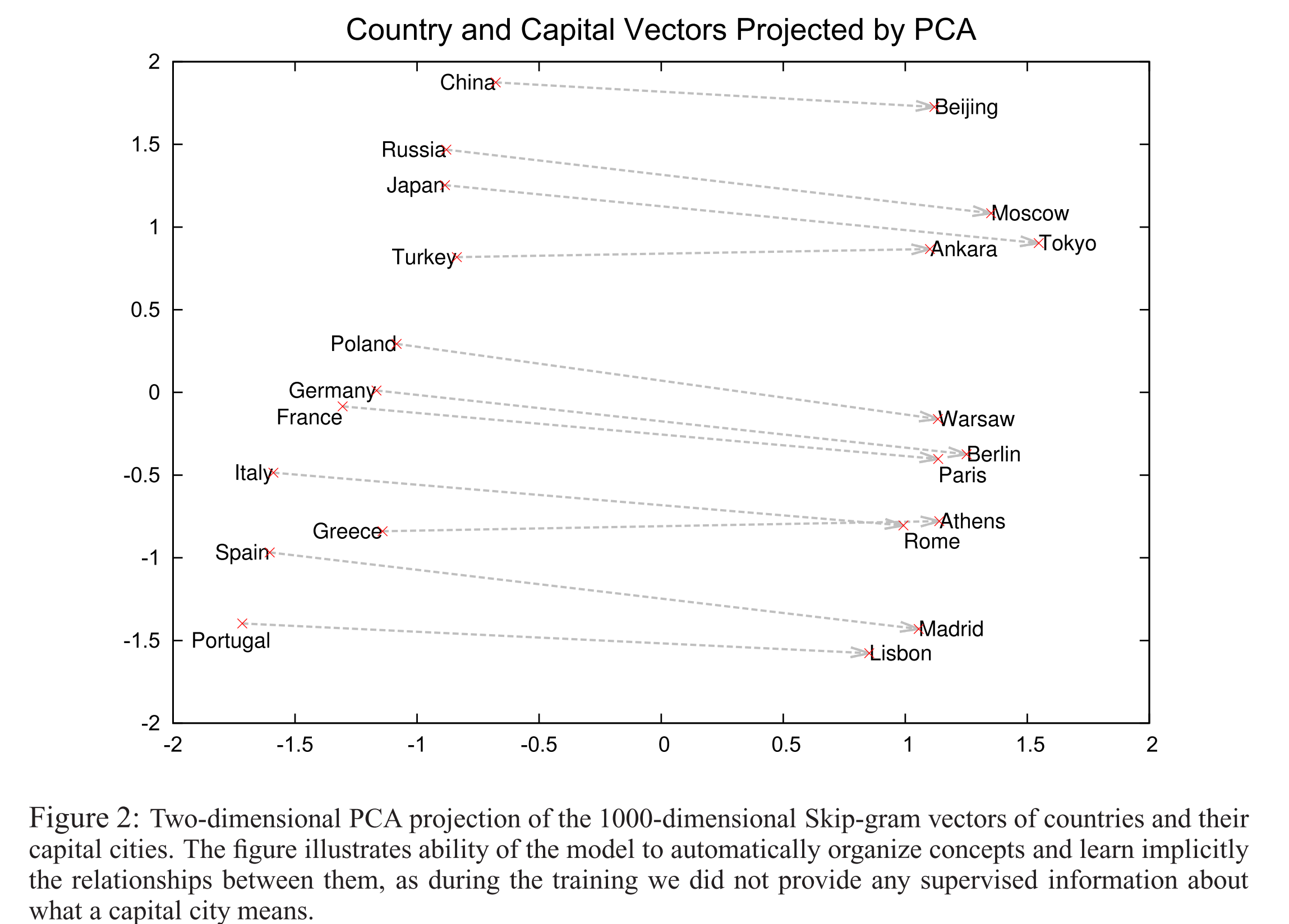
Here are some more examples of the ‘a is to b as c is to ?’ style questions answered by word vectors:

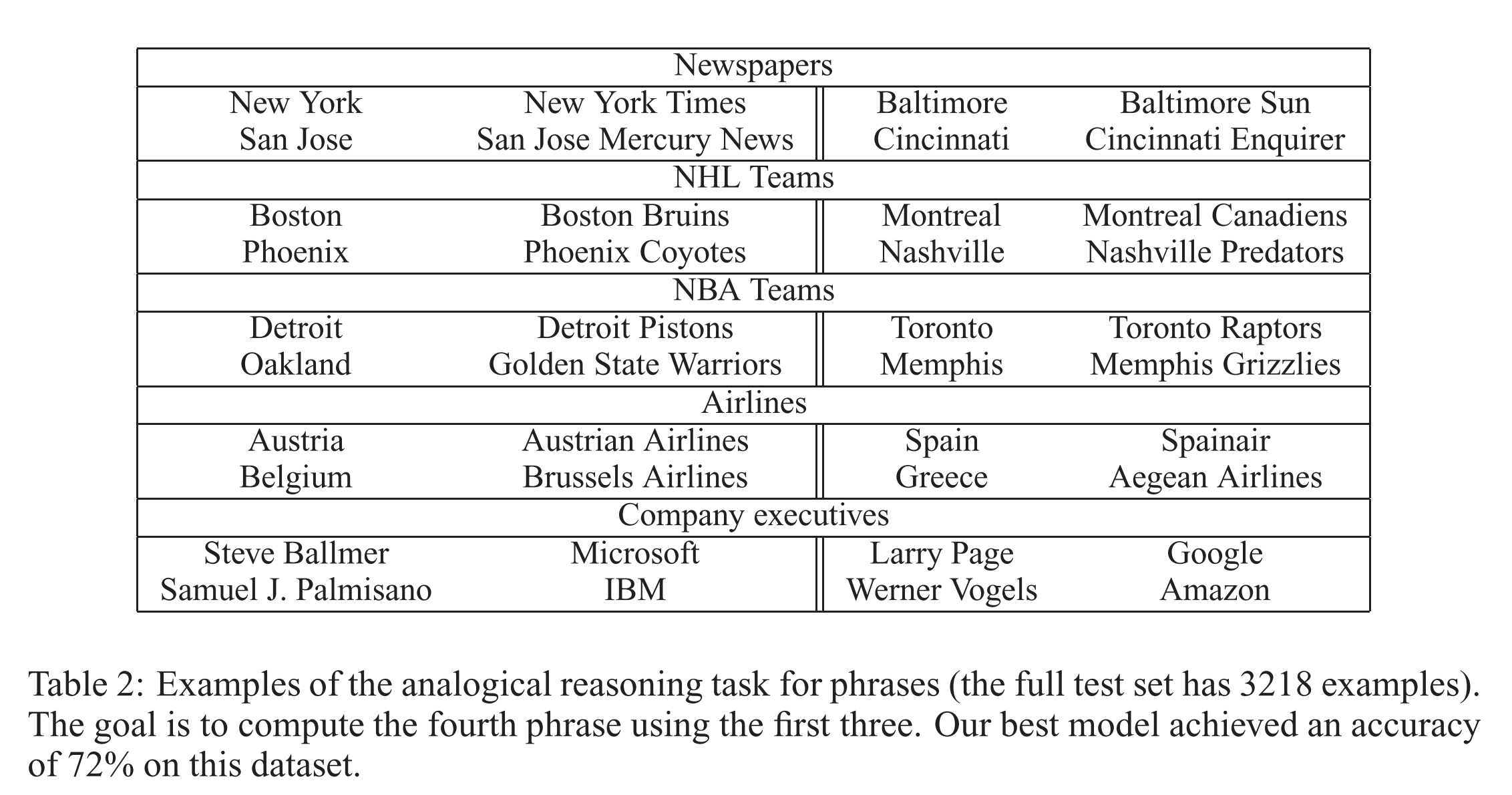
We can also use element-wise addition of vector elements to ask questions such as ‘German + airlines’ and by looking at the closest tokens to the composite vector come up with impressive answers:

Word vectors with such semantic relationships could be used to improve many existing NLP applications, such as machine translation, information retrieval and question answering systems, and may enable other future applications yet to be invented.

The Semantic-Syntatic word relationship tests for understanding of a wide variety of relationships as shown below. Using 640-dimensional word vectors, a skip-gram trained model achieved 55% semantic accuracy and 59% syntactic accuracy.