 Is Regression Analysis Really Machine Learning?
Is Regression Analysis Really Machine Learning?
What separates "traditional" applied statistics from machine learning? Is statistics the foundation on top of which machine learning is built? Is machine learning a superset of "traditional" statistics? Do these 2 concepts have a third unifying concept in common? So, in that vein... is regression analysis actually a form of machine learning?
What separates statistics from machine learning?
That's a broad topic which has been treated many times. Much of what has been written on this topic is good, much is bad. But I find that the stats vs. machine learning argument, at that level, tends to focus on the forest at the cost of completely overlooking the trees.
For example, Aatash Shah has written:
- Machine Learning is an algorithm that can learn from data without relying on rules-based programming.
- Statistical modeling is a formalization of relationships between variables in the data in the form of mathematical equations.
Shah's definitions, which I believe are reflective of many approaches, tend to focus on different ends of the respective spectrums of each of these concepts, treating machine learning as a practical activity and statistics as a theoretical abstraction (and, yes, I'm lumping "statistical modeling" together with "statistics" in this case... at least, for now). The relationship between statistics and machine learning is actually a highly complex one, and merely defining the 2 concepts is not helpful in dissecting this connection.
Waxing philosophic on this broad topic can quickly turn to pontification:
- Is statistics the foundation on top of which machine learning is built?
- Is machine learning a superset of "traditional" statistics?
- Do these 2 concepts have a third unifying concept in common?
I believe that such a high level approach, framed in this way, is both misguided and, ultimately, a waste of time. Even if you are interested in exploring such a topic, looking at more specific questions can likely bear more fruit, and possibly (hopefully?) lead to more concrete conclusions. Also, a more accurate framing is that of statistical versus machine learning models.
So, in that vein... is regression analysis actually a form of machine learning?
Gregory Piatetsky-Shapiro, President of KDnuggets, had this to share when I asked him his thoughts on this more specific topic, dispelling the notion that regression may be too "simple" to be considered machine learning:
"Traditional" linear regression may be considered by some Machine Learning researchers to be too simple to be considered "Machine Learning", and to be merely "Statistics" but I think the boundary between Machine Learning and Statistics is artificial. C4.5 decision tree algorithm is also not too complicated but it is probably considered to be Machine Learning.
More advanced algorithms arise from linear regression, such as ridge regression, least angle regression, and LASSO, which are probably used by many Machine Learning researchers, and to properly understand them, you need to understand the basic Linear Regression.
So, yes, Linear Regression should be a part of the toolbox of any Machine Learning researcher.
I asked Prof. Dr. Diego Kuonen, CStat PStat CSci -- CEO and CAO, Statoo Consulting, Switzerland & Professor of Data Science, University of Geneva, Switzerland -- his thoughts, and he was kind enough to provide the following insight:
Every supervised analytics model (from statistics, data science and/or machine learning) makes assumptions concerning how the distribution of the output (or some aspect of it) depends on the model inputs. If no assumptions whatsoever would be made, there is no rational basis to generalise beyond the data observed.
As such, it makes sense to base conclusions only on valid models (i.e. where the assumptions were verified). In other words, any conclusion is only as sound as the model on which it is based.
This takes a less-divisive, more unifying approach, if you will, treating both statistical and machine learning models as tools toward the ultimate goal: understanding data. Diego seems much less concerned with which tool is used, focusing instead on ensuring that the tool is used properly, a valid model is built, and the result is an increased understanding of the data. Debating exactly how statistics relates to machine learning is useless if the resulting generalizations are based on invalid models, regardless of the approach used in building them.
I, personally, have spent a lot of time pondering these very questions over the years. Since my first exposure to both linear regression and, to a lesser extent, decision trees -- from the perspective of data mining books and courses -- I was originally flabbergasted that these simple concepts could be considered "machine learning." This was especially so given that I had already been familiar with regression from statistics for quite some time at that point, and no one had ever mentioned the term "machine learning" to me in any of these previous learning scenarios. I imagine that this is a similar reaction that others in my position have had at similar periods of their educations and/or careers.
For some quick context, as I have also considered at length the relationship between data mining and machine learning -- which can also become an act of futility -- I like to think of data mining as a process, and machine learning as the tool which facilitates this process. Adding in that a modern definition of statistics (via Kuonen) is "the science of learning from data (or making sense out of data), and of measuring, controlling and communicating uncertainty," I am happy with the quick-and-dirty definition of data mining as "high speed statistical analysis at scale."
A similarly simplified definition is that machine learning is made up of 3 things: 1) data, 2) a model or estimator, and 3) a cost or loss to minimize. The entire raison dêtre of machine learning is the process of optimizing a loss function, which takes similar statistical problems which humans can solve by hand and greatly increases the amount and/or nature of data which can be entertained.
So, getting back to the original question (again), does linear regression -- the simplest form of regression analysis -- meet these requirements?
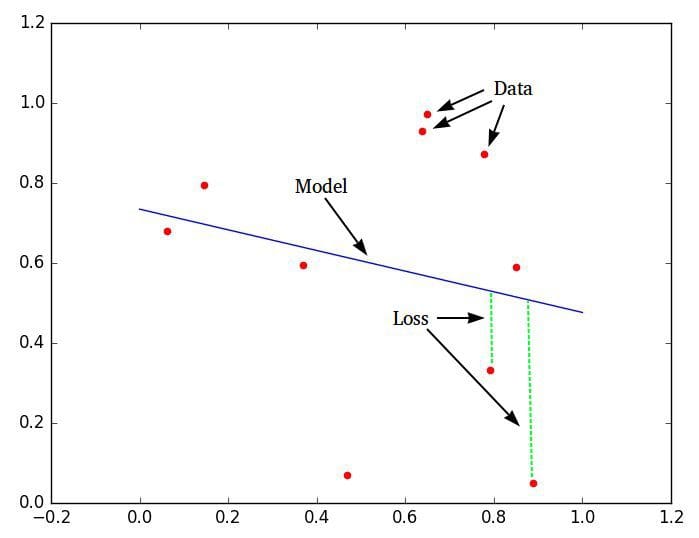
It would appear so!
Of course, this doesn't close the case, as it were. If I have a set of 10 data points, plot 9 of them, holding the 10th back for "testing," and I solve an equation and plot the results by hand, is this machine learning? If it is not -- and it clearly isn't -- where does the transition to machine learning occur? 100 data points? A significant enough number of instance attributes? Simply the use of a computer? I prefer to think of "traditional" statistics and machine learning as being at opposite ends of a spectrum, and the blurred area of transition between the 2 as being permanently undefined and undefinable.
As an aside, and in contrast to the above, Mike Yeomans has written of machine learning that we should "[t]hink of it simply as a branch of statistics, designed for a world of big data," an opinion which Kuonen has shown some appreciation for. Kuonen has also noted that while one could argue that "data mining is statistics at scale and speed" (Daryl Pregibon, 1999), he notes that there is a difference in their approaches, which you can read about here.
I’ll give the final word to Kevin Gray, President of Cannon Gray, to whom I reached out for comment. He nicely put a button on the topic, wondering if this whole discussion is even necessary.
My position is that I don't know but wonder if it matters. I'm no good at region, patriotism and that sort of thing. If it feels good (enough), do it! :-)
Along with the other contributors, I would like to particularly thank Prof. Dr. Diego Kuonen for both his input and feedback while writing this.
Related:
- Linear Regression, Least Squares & Matrix Multiplication: A Concise Technical Overview
- Regression Analysis: A Primer
- Big Data, Bible Codes, and Bonferroni

 Is Regression Analysis Really Machine Learning?
Is Regression Analysis Really Machine Learning?