Estimating an Optimal Learning Rate For a Deep Neural Network
This post describes a simple and powerful way to find a reasonable learning rate for your neural network.
By Pavel Surmenok, Engineering Manager at JustAnswer.

Source: https://www.hellobc.com.au/british-columbia/things-to-do/winter-activities/skiing-snowboarding.aspx
The learning rate is one of the most important hyper-parameters to tune for training deep neural networks.
In this post, I’m describing a simple and powerful way to find a reasonable learning rate that I learned from fast.ai Deep Learning course. I’m taking the new version of the course in person at University of San Francisco. It’s not available to the general public yet, but will be at the end of the year at course.fast.ai (which currently has the last year’s version).
How does learning rate impact training?
Deep learning models are typically trained by a stochastic gradient descent optimizer. There are many variations of stochastic gradient descent: Adam, RMSProp, Adagrad, etc. All of them let you set the learning rate. This parameter tells the optimizer how far to move the weights in the direction of the gradient for a mini-batch.
If the learning rate is low, then training is more reliable, but optimization will take a lot of time because steps towards the minimum of the loss function are tiny.
If the learning rate is high, then training may not converge or even diverge. Weight changes can be so big that the optimizer overshoots the minimum and makes the loss worse.
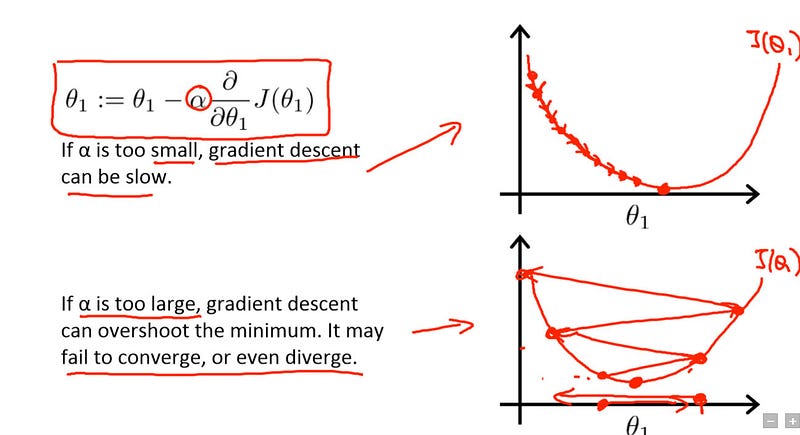
Gradient descent with small (top) and large (bottom) learning rates. Source: Andrew Ng’s Machine Learning course on Coursera
The training should start from a relatively large learning rate because, in the beginning, random weights are far from optimal, and then the learning rate can decrease during training to allow more fine-grained weight updates.
There are multiple ways to select a good starting point for the learning rate. A naive approach is to try a few different values and see which one gives you the best loss without sacrificing speed of training. We might start with a large value like 0.1, then try exponentially lower values: 0.01, 0.001, etc. When we start training with a large learning rate, the loss doesn’t improve and probably even grows while we run the first few iterations of training. When training with a smaller learning rate, at some point the value of the loss function starts decreasing in the first few iterations. This learning rate is the maximum we can use, any higher value doesn’t let the training converge. Even this value is too high: it won’t be good enough to train for multiple epochs because over time the network will require more fine-grained weight updates. Therefore, a reasonable learning rate to start training from will be probably 1–2 orders of magnitude lower.
There must be a smarter way
Leslie N. Smith describes a powerful technique to select a range of learning rates for a neural network in section 3.3 of the 2015 paper “Cyclical Learning Rates for Training Neural Networks”.
The trick is to train a network starting from a low learning rate and increase the learning rate exponentially for every batch.
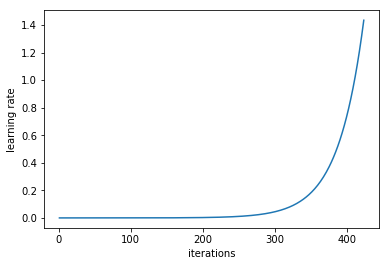
Learning rate increases after each mini-batch
Record the learning rate and training loss for every batch. Then, plot the loss and the learning rate. Typically, it looks like this:
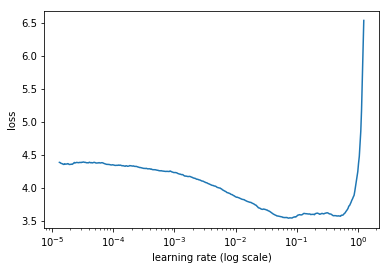
The loss decreases in the beginning, then the training process starts diverging
First, with low learning rates, the loss improves slowly, then training accelerates until the learning rate becomes too large and loss goes up: the training process diverges.
We need to select a point on the graph with the fastest decrease in the loss. In this example, the loss function decreases fast when the learning rate is between 0.001 and 0.01.
Another way to look at these numbers is calculating the rate of change of the loss (a derivative of the loss function with respect to iteration number), then plot the change rate on the y-axis and the learning rate on the x-axis.
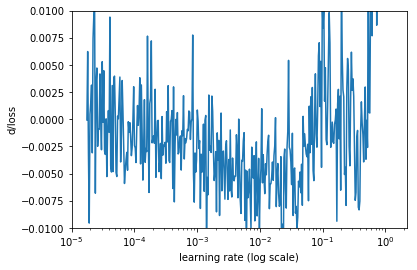
Rate of change of the loss
It looks too noisy, let’s smooth it out using simple moving average.
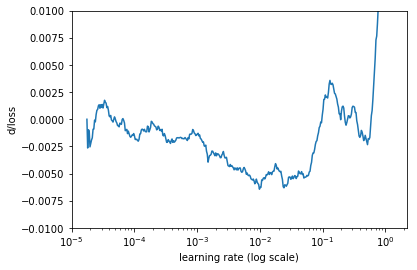
Rate of change of the loss, simple moving average
This looks better. On this graph, we need to find the minimum. It is close to lr=0.01.
Implementation
Jeremy Howard and his team at USF Data Institute developed fast.ai, a deep learning library that is a high-level abstraction on top of PyTorch. It’s an easy to use and yet powerful toolset for training state of the art deep learning models. Jeremy uses the library in the latest version of the Deep Learning course (fast.ai).
The library provides an implementation of the learning rate finder. You need just two lines of code to plot the loss over learning rates for your model:
The library doesn’t have the code to plot the rate of change of the loss function, but it’s trivial to calculate:
Note that selecting a learning rate once, before training, is not enough. The optimal learning rate decreases while training. You can rerun the same learning rate search procedure periodically to find the learning rate at a later point in the training process.
Implementing the method using other libraries
I haven’t seen ready to use implementations of this learning rate search method for other libraries like Keras, but it should be trivial to write. Just run the training multiple times, one mini-batch at a time. Increase the learning rate after each mini-batch by multiplying it by a small constant. Stop the procedure when the loss gets a lot higher than the previously observed best value (e.g., when current loss > best loss * 4).
There is more to it
Selecting a starting value for the learning rate is just one part of the problem. Another thing to optimize is the learning schedule: how to change the learning rate during training. The conventional wisdom is that the learning rate should decrease over time, and there are multiple ways to set this up: step-wise learning rate annealing when the loss stops improving, exponential learning rate decay, cosine annealing, etc.
The paper that I referenced above describes a novel way to change the learning rate cyclically. This method improves performance of convolutional neural networks on a variety of image classification tasks.
Please send me a message if you know other interesting tips and tricks for training deep neural networks.
Bio: Pavel Surmenok is Engineering Manager at JustAnswer.
Original. Reposted with permission.
Related:
