Detecting Breast Cancer with Deep Learning
Breast cancer is the most common invasive cancer in women, and the second main cause of cancer death in women, after lung cancer. In this article I will build a WideResNet based neural network to categorize slide images into two classes, one that contains breast cancer and other that doesn’t using Deep Learning Studio.

Invasive ductal carcinoma (IDC) also known as infiltrating ductal carcinoma is most common type of breast cancer. American Cancer Society estimates more than 180,000 women in the United States find out they have invasive breast cancer every year. Most of these cancers are diagnosed with IDC.
Accurately identifying and categorizing breast cancer subtype is an important task. Automated methods based on AI can significantly save time and reduce error.
In this article I will be building a WideResNet based neural network to categorize slide images to two classes one that contains breast cancer and other that don’t using the Deep Learning Studio.
If you are not familiar with Deep Learning take a look at this :)
And if you want to know more about Deep Cognition see this:
About the Dataset
Dataset for this problem has been collected by researcher at Case Western Reserve University in Cleveland, Ohio. Original dataset is available here (Edit: the original link is not working anymore, download from Kaggle). This dataset is preprocessed by nice people at Kaggle that was used as starting point in our work.
Each slide approximately yields 1700 images of 50x50 patches
There are 162 whole mount slides images available in the dataset. These slides have been scanned at 40x resolution. Finally, those slides then are divided 275,215 50x50 pixel patches. Then one label of 0 or 1 is assigned to each of these patches. For patches that include IDC has label of 1 and patches that don’t include IDC have label of 0.
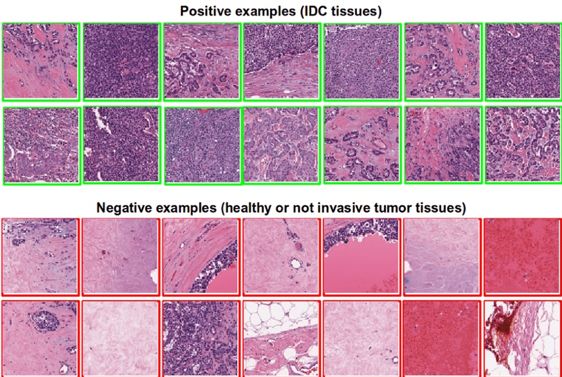
3 Example of positive and negative IDC tissue. https://doi.org/10.1117/12.2043872
Classifying Slides with a WideResNet
ResNet architecture that uses residual connections have been very successful at image classification tasks. WideResNet architecture has shown that similar performance can be achieved with much less depth as small as 16 layers deep. This helps in solving various problems associated with very deep ResNets like exploding/vanishing gradients and degradation.
Using the great information in the blogs by Vincent Fung and Apil Tamang we can get some intuiton about what a ResNet is actually doing.
The core idea of ResNet is introducing a so-called “identity shortcut connection” that skips one or more layers.
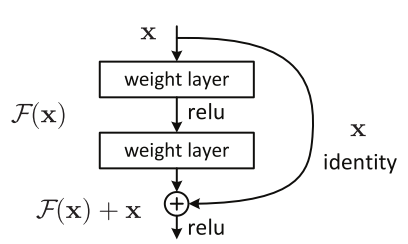
Residual Block
The original authors of the paper hypothesized that letting the stacked layers fit a residual mapping is easier than letting them directly fit the desired underlaying mapping. This indicates that the deeper model should not produce a training error higher than its shallower counterparts.
Because of its compelling results, ResNet quickly became one of the most popular architectures in various computer vision tasks.
Now a WideResNet exist for a reason: each fraction of a percent of improved accuracy costs nearly doubling the number of layers, and so training very deep residual networks has a problem of diminishing feature reuse, which makes these networks very slow to train.
https://dl.acm.org/citation.cfm?doid=2988450.2988454
To tackle these problems Zagoruyko and Komodakis conducted a detailed experimental study on the architecture of ResNet blocks (published in 2016), based on which they proposed a novel architecture where we decrease depth and increase width of residual networks. They called them Wide Residual Networks.
Now we will show step by step process of solving this problem using WideResNet architecture. We are using Deep Learning Studio that allows us to build neural network rapidly without need to worry about coding, syntax and dataset ingestion.
1. Project Creation
After you log in to Deep Learning Studio that is either running locally or in cloud click on + button to create a new project.
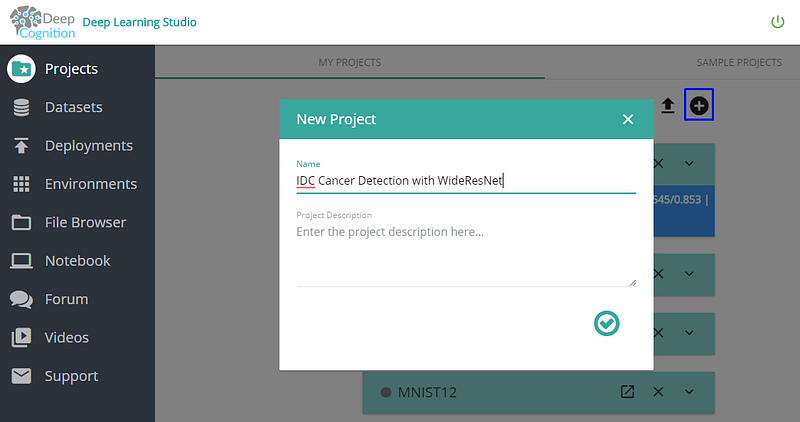
2. Dataset Intake
We then setup dataset for this project in “Data” tab. Usually 80% — 20% is a good split between training and validation but you can use other setting if you prefer. Also don’t forget to set Load Dataset in Memory to “Full dataset” if your machine has enough RAM to load full dataset in RAM.
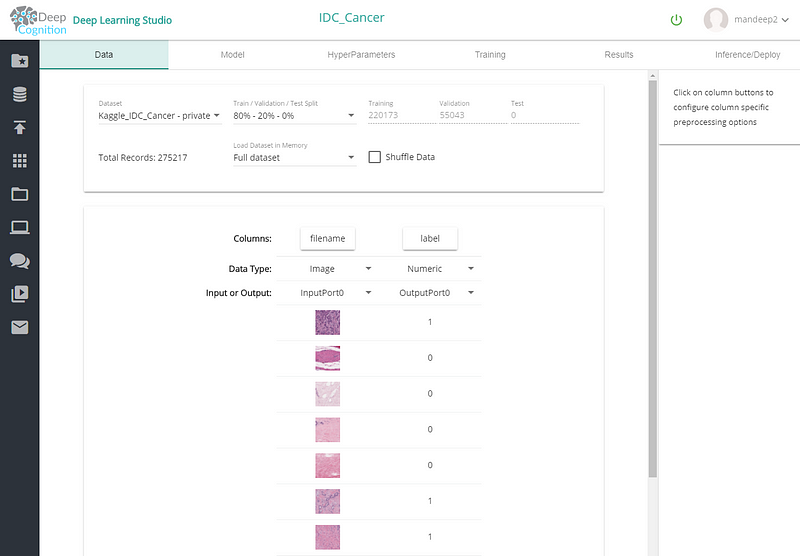
3. Create the Neural Network
You can create a neural network as shown below by dragging and dropping the layers.
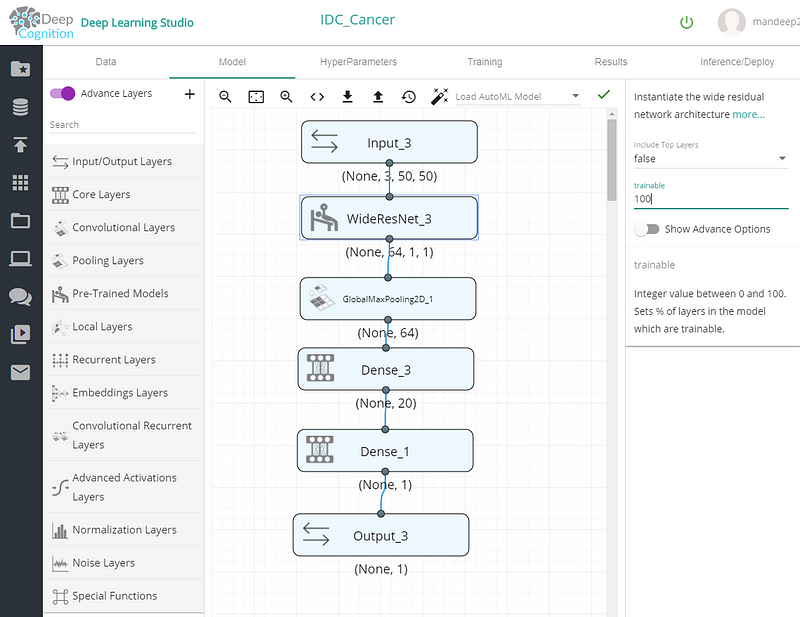
Make sure to set WideResNet 100% trainable from the properties on the right side. Also first Dense layer (Dense_3) should have 20 or so neurons with ReLU as activation function. Final Dense layer (Dense_1) should have output dimension as 1 and activation as sigmoid. Reason of this is because we have setup this problem as a regression instead of classification. If the regression output is below 0.5 then we can say that input belongs to class 0 (no IDC cancer), or else it has IDC cancer.
4. Hyperparameter and Training
Hyperparameters that we used are shown below. Feel free to change and experiment with them.
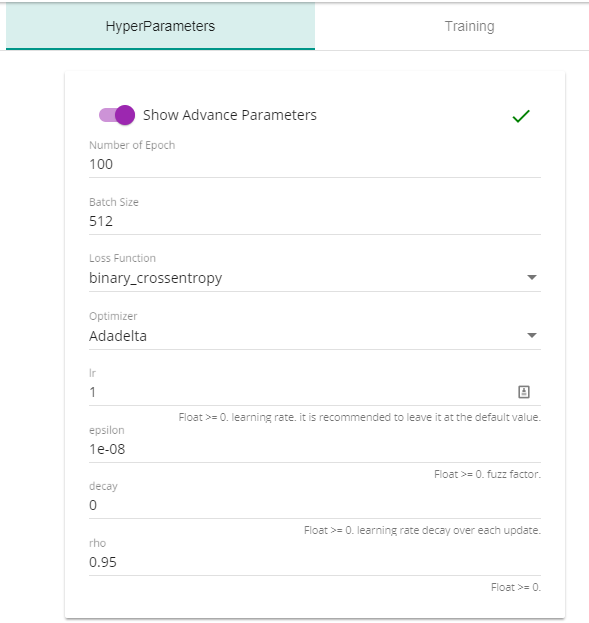
Finally, you can start the training from Training Tab and monitor the progress with training dashboard.
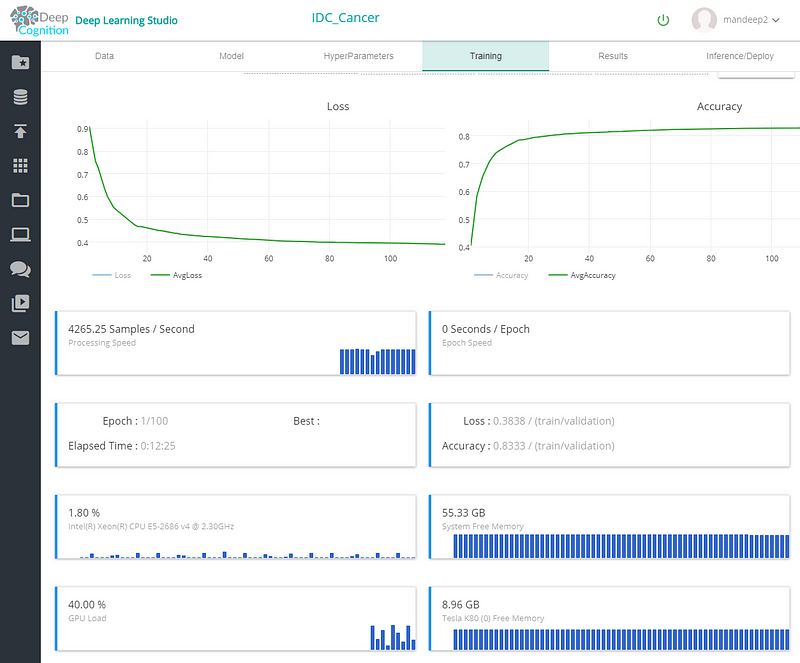
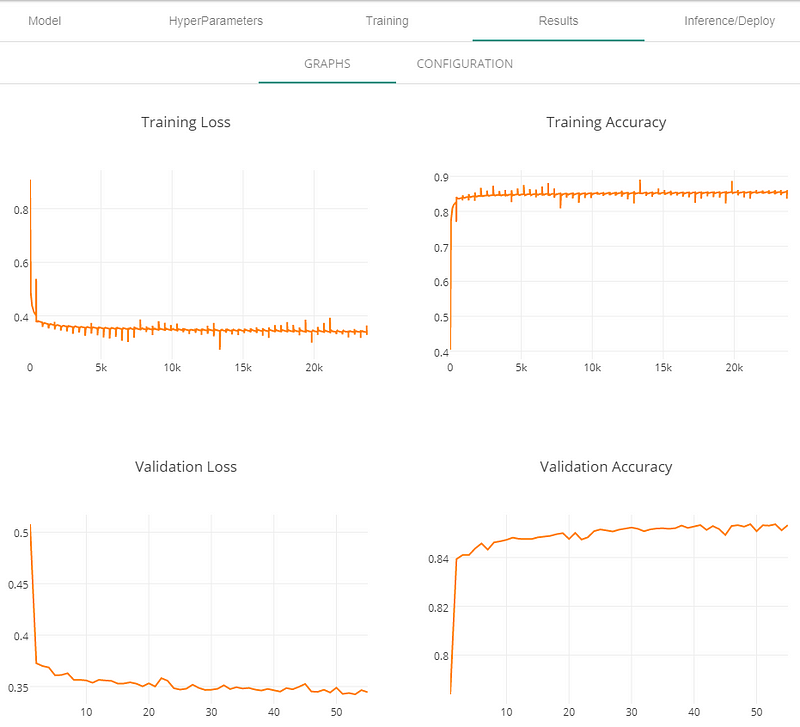
Once you complete your training you can check the results in results tab. We achieved more than 85% accuracy in matter of couple of hours on a K80 GPU that costs about $0.90 per hour.
With Deep Learning Studio deployment as a webapp or REST API is child’s play can be done using deploy tab as shown below.
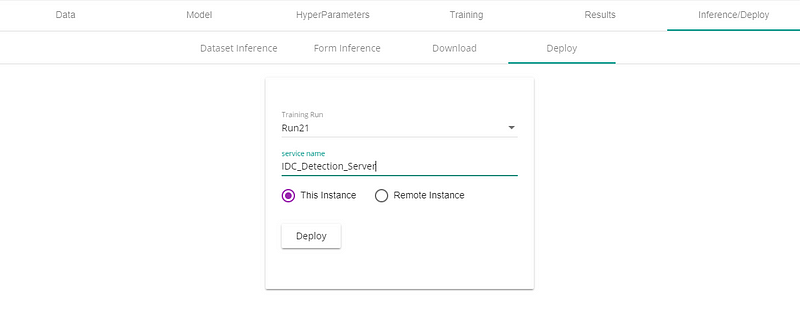
5. Deploying the model
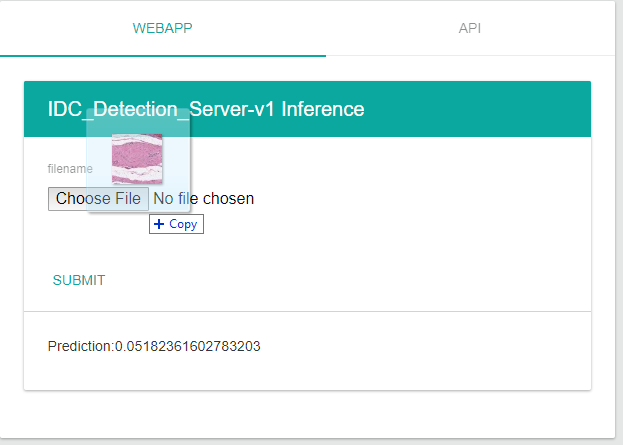
Deployed model can be accessed as WebApp or REST API as shown below:
Concluding Remarks
So you can see that a Deep Learning model can be built in minutes and deployed in seconds with Deep Learning Studio. Such power will enable many developers to tackle complex problem without worrying about coding, API etc.
I’ll repeat here what I said in the “Deep Learning made easy with Deep Cognition” blog about the “Black-Box problem”:
Something that will come yo your mind is: ok I’m doing deep learning but I have no idea how.
Actually you can download the code that produced the predictions, and as you will see it is written in Keras. You can then upload the code and test it with the notebook that the system provides.
The AutoML features and the GUI have the best of Keras and other DL frameworks in a simple click, and the good thing about it is that it chooses the best practices for DL for you, and if you are not completely happy with the choices you can change them really easy in the UI or interact with the notebook.
This system is built with the premise of making AI easy for everyone, you don’t have to be an expert when creating this complex models, but my recommendation is that is good that you have an idea of what you are doing, read some of the TensorFlow or Keras documentation, watch some videos and be informed. If you are an expert in the subject great! This will make your life much easier and you can still apply your expertise when building the models.
Thanks to Deep Cognition for helping me build this article :)
Thanks for reading this. I hope you found something interesting here :)
If you have questions just add me in twitter:
and LinkedIn:
See you there :)
Bio: Favio Vazquez is a physicist and computer engineer working on Big Data and Computational Cosmology. He has a passion for science, philosophy, programming, and Data Science. Right now he is working on data science, machine learning and big data as the Principal Data Scientist at Oxxo. Also, he is the creator of Ciencia y Datos, a Data Science publication in Spanish. he loves new challenges, working with a good team and having interesting problems to solve. He is part of Apache Spark collaboration, helping in MLLib, Core and the Documentation. He loves applying his knowledge and expertise in science, data analysis, visualization and data processing to help the world become a better place.
Original. Reposted with permission.
Related:
- A “Weird” Introduction to Deep Learning
- My Journey into Deep Learning
- Data Science vs Addiction: Estimating Opioid Abuse by Location
