Exploring Unsupervised Learning Metrics
Improves your data science skill arsenals with these metrics.
Image by rawpixel on Freepik
Unsupervised learning is a branch of machine learning where the models learn patterns from the available data rather than provided with the actual label. We let the algorithm come up with the answers.
In unsupervised learning, there are two main techniques; clustering and dimensionality reduction. The clustering technique uses an algorithm to learn the pattern to segment the data. In contrast, the dimensionality reduction technique tries to reduce the number of features by keeping the actual information intact as much as possible.
An example algorithm for clustering is K-Means, and for dimensionality reduction is PCA. These were the most used algorithm for unsupervised learning. However, we rarely talk about the metrics to evaluate unsupervised learning. As useful as it is, we still need to evaluate the result to know if the output is precise.
This article will discuss the metrics used to evaluate unsupervised machine learning algorithms and will be divided into two sections; Clustering algorithm metrics and dimensionality reduction metrics. Let’s get into it.
Clustering Algorithm Metrics
We would not discuss in detail about the clustering algorithm as it’s not the main point of this article. Instead, we would focus on examples of the metrics used for the evaluation and how to assess the result.
This article will use the Wine Dataset from Kaggle as our dataset example. Let’s read the data first and use the K-Means algorithm to segment the data.
import pandas as pd
from sklearn.cluster import KMeans
df = pd.read_csv('wine-clustering.csv')
kmeans = KMeans(n_clusters=4, random_state=0)
kmeans.fit(df)
I initiate the cluster as 4, which means we segment the data into 4 clusters. Is it the right number of clusters? Or is there any more suitable cluster number? Commonly, we can use the technique called the elbow method to find the appropriate cluster. Let me show the code below.
wcss = []
for k in range(1, 11):
kmeans = KMeans(n_clusters=k, random_state=0)
kmeans.fit(df)
wcss.append(kmeans.inertia_)
# Plot the elbow method
plt.plot(range(1, 11), wcss, marker='o')
plt.xlabel('Number of Clusters (k)')
plt.ylabel('WCSS')
plt.title('Elbow Method')
plt.show()
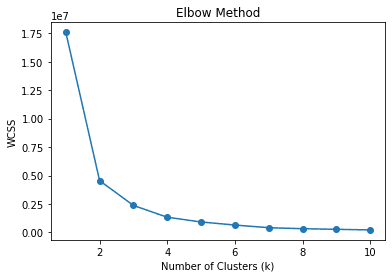
In the elbow method, we use WCSS or Within-Cluster Sum of Squares to calculate the sum of squared distances between data points and the respective cluster centroids for various k (clusters). The best k value is expected to be the one with the most decrease of WCSS or the elbow in the picture above, which is 2.
However, we can expand the elbow method to use other metrics to find the best k. How about the algorithm automatically finding the cluster number without relying on the centroid? Yes, we can also evaluate them using similar metrics.
As a note, we can assume a centroid as the data mean for each cluster even though we don’t use the K-Means algorithm. So, any algorithm that did not rely on the centroid while segmenting the data could still use any metric evaluation that relies on the centroid.
Silhouette Coefficient
Silhouette is a technique in clustering to measure the similarity of data within the cluster compared to the other cluster. The Silhouette coefficient is a numerical representation ranging from -1 to 1. Value 1 means each cluster completely differed from the others, and value -1 means all the data was assigned to the wrong cluster. 0 means there are no meaningful clusters from the data.
We could use the following code to calculate the Silhouette coefficient.
# Calculate Silhouette Coefficient
from sklearn.metrics import silhouette_score
sil_coeff = silhouette_score(df.drop("labels", axis=1), df["labels"])
print("Silhouette Coefficient:", round(sil_coeff, 3))
Silhouette Coefficient: 0.562
We can see that our segmentation above has a positive Silhouette Coefficient, which means there is the degree of separation between the clusters, although some overlapping still happens.
Calinski-Harabasz Index
The Calinski-Harabasz Index or Variance Ratio Criterion is an index that is used to evaluate cluster quality by measuring the ratio of between-cluster dispersion to within-cluster dispersion. Basically, we measured the differences between the sum squared distance of the data between the cluster and data within the internal cluster.
The higher the Calinski-Harabasz Index score, the better, which means the clusters were well separated. However, there are no upper limits for the score means that this metric is better for evaluating different k numbers rather than interpreting the result as it is.
Let’s use the Python code to calculate the Calinski-Harabasz Index score.
# Calculate Calinski-Harabasz Index
from sklearn.metrics import calinski_harabasz_score
ch_index = calinski_harabasz_score(df.drop('labels', axis=1), df['labels'])
print("Calinski-Harabasz Index:", round(ch_index, 3))
Calinski-Harabasz Index: 708.087
One other consideration for the Calinski-Harabasz Index score is that the score is sensitive to the number of clusters. A higher number of clusters could lead to a higher score as well. So it’s a good idea to use other metrics alongside the Calinski-Harabasz Index to validate the result.
Davies-Bouldin Index
The Davies-Bouldin Index is a clustering evaluation metric measured by calculating the average similarity between each cluster and its most similar one. The ratio of within-cluster distances to between-cluster distances calculates the similarity. This means the further apart the clusters and the less dispersed would lead to better scores.
In contrast with our previous metrics, the Davies-Bouldin Index aims to have a lower score as much as possible. The lower the score was, the more separated each cluster was. Let’s use a Python example to calculate the score.
# Calculate Davies-Bouldin Index
from sklearn.metrics import davies_bouldin_score
dbi = davies_bouldin_score(df.drop('labels', axis=1), df['labels'])
print("Davies-Bouldin Index:", round(dbi, 3))
Davies-Bouldin Index: 0.544
We can’t say that the above score is good or bad because similar to the previous metrics, we still need to evaluate the result by using various metrics as support.
Dimensionality Reduction Metrics
Unlike clustering, dimensionality reduction aims to reduce the number of features while preserving the original information as much as possible. Because of that, many of the evaluation metrics in dimensionality reduction were all about information preservation. Let’s reduce dimensionality with PCA and see how the metric works.
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
#Scaled the data
scaler = StandardScaler()
df_scaled = scaler.fit_transform(df)
pca = PCA()
pca.fit(df_scaled)
In the above example, we fit the PCA to the data, but we haven’t reduced the number of the feature yet. Instead, we want to evaluate the dimensionality reduction and variance trade-off with the Cumulative Explained Variance. It’s the common metric for dimensionality reduction to see how information remains with each feature reduction.
#Calculate Cumulative Explained Variance
cev = np.cumsum(pca.explained_variance_ratio_)
plt.plot(range(1, len(cev) + 1), cev, marker='o')
plt.xlabel('Number of PC')
plt.ylabel('CEV')
plt.title('CEV vs. Number of PC')
plt.grid()
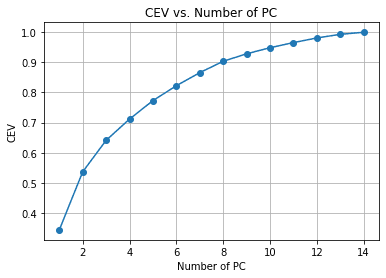
We can see from the above chart the amount of PC retained compared to the explained variance. As a rule of thumb, we often choose around 90-95% retained when we try to make dimensionality reduction, so around 14 features are reduced to 8 if we follow the chart above.
Let’s look at the other metrics to validate our dimensionality reduction.
Trustworthiness
Trustworthiness is a measurement of the dimensionality reduction technique quality. This metric measured how well the reduced dimension preserved the original data nearest neighbor.
Basically, the metric tries to see how well the dimension reduction technique preserved the data in maintaining the original data's local structure.
The Trustworthiness metric ranges between 0 to 1, where values closer to 1 are means the neighbor that is close to reduced dimension data points are mostly close as well in the original dimension.
Let’s use the Python code to calculate the Trustworthiness metric.
from sklearn.manifold import trustworthiness
# Calculate Trustworthiness. Tweak the number of neighbors depends on the dataset size.
tw = trustworthiness(df_scaled, df_pca, n_neighbors=5)
print("Trustworthiness:", round(tw, 3))
Trustworthiness: 0.87
Sammon’s Mapping
Sammon’s mapping is a non-linear dimensionality reduction technique to preserve the high-dimensionality pairwise distance when being reduced. The objective is to use Sammon’s Stress function to calculate the pairwise distance between the original data and the reduction space.
The lower Sammon’s stress function score, the better because it indicates better pairwise preservation. Let’s try to use the Python code example.
First, we would install an additional package for Sammon’s Mapping.
pip install sammon-mapping
Then we would use the following code to calculate the Sammon’s stress.
# Calculate Sammon's Stress
from sammon import sammon
pca_res, sammon_st = sammon.sammon(np.array(df))
print("Sammon's Stress:", round(sammon_st, 5))
Sammon's Stress: 1e-05
The result shown a low Sammon’s Score which means the data preservation was there.
Conclusion
Unsupervised learning is a machine learning branch that tries to learn the pattern from the data. Compared to supervised learning, the output evaluation might not discuss much. In this article, we try to learn a few unsupervised learning metrics, including:
- Within-Cluster Sum Square
- Silhouette Coefficient
- Calinski-Harabasz Index
- Davies-Bouldin Index
- Cumulative Explained Variance
- Trustworthiness
- Sammon’s Mapping
Cornellius Yudha Wijaya is a data science assistant manager and data writer. While working full-time at Allianz Indonesia, he loves to share Python and Data tips via social media and writing media.
