Machine Learning Evaluation Metrics: Theory and Overview
High-level exploration of evaluation metrics in machine learning and their importance.

Illustration by Author
Building a machine learning model that generalizes well on new data is very challenging. It needs to be evaluated to understand if the model is enough good or needs some modifications to improve the performance.
If the model doesn’t learn enough of the patterns from the training set, it will perform badly on both training and test sets. This is the so-called underfitting problem.
Learning too much about the patterns of training data, even the noise, will lead the model to perform very well on the training set, but it will work poorly on the test set. This situation is overfitting. The generalization of the model can be obtained if the performances measured both in training and test sets are similar.
In this article, we are going to see the most important evaluation metrics for classification and regression problems that will help to verify if the model is capturing well the patterns from the training sample and performing well on unknown data. Let’s get started!
Classification
When our target is categorical, we are dealing with a classification problem. The choice of the most appropriate metrics depends on different aspects, such as the characteristics of the dataset, whether it’s imbalanced or not, and the goals of the analysis.
Before showing the evaluation metrics, there is an important table that needs to be explained, called Confusion Matrix, that summarizes well the performance of a classification model.
Let’s say that we want to train a model to detect breast cancer from an ultrasound image. We have only two classes, malignant and benign.
- True Positives: The number of terminally ill people that are predicted to have a malignant cancer
- True Negatives: The number of healthy people that are predicted to have a benign cancer
- False Positives: The number of healthy people that are predicted to have malignant cancer
- False Negatives: The number of terminally ill people that predicted to have benign cancer

Example of Confusion Matrix. Illustration by Author.
Accuracy

Accuracy is one of the most known and popular metrics to evaluate a classification model. It is the fraction of the corrected predictions divided by the number of Samples.
The Accuracy is employed when we are aware that the dataset is balanced. So, each class of the output variable has the same number of observations.
Using Accuracy, we can answer the question “Is the model predicting correctly all the classes?”. For this reason, we have the correct predictions of both the positive class (malignant cancer) and the negative class (benign cancer).
Precision

Differently from Accuracy, Precision is an evaluation metric for classification used when the classes are imbalanced.
Precision answer to the following question: “What proportion of malignant cancer identifications was actually correct?”. It’s calculated as the ratio between True Positives and Positive Predictions.
We are interested in using Precision if we are worried about False Positives and we want to minimize it. It would be better to avoid running the lives of healthy people with fake news of a malignant cancer.
The lower the number of False Positives, the higher the Precision will be.
Recall

Together with Precision, Recall is another metric applied when the classes of the output variable have a different number of observations. Recall answers to the following question: “What proportion of patients with malignant cancer I was able to recognize?”.
We care about Recall if our attention is focused on the False Negatives. A false negative means that that patient has a malignant cancer, but we weren’t able to identify it. Then, both Recall and Precision should be monitored to obtain the desirable good performance on unknown data.
F1-Score
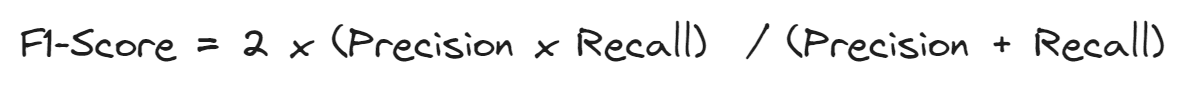
Monitoring both Precision and Recall can be messy and it would be preferable to have a measure that summarizes both these measures. This is possible with the F1-score, which is defined as the harmonic mean of precision and recall.
A high f1-score is justified by the fact that both Precision and Recall have high values. If recall or precision has low values, the f1-score will be penalized and, then, will have a low value too.
Regression

Illustration by Author
When the output variable is numerical, we are dealing with a regression problem. As in the classification problem, it’s crucial to choose the metric for evaluating the regression model, depending on the purposes of the analysis.
The most popular example of a regression problem is the prediction of house prices. Are we interested in predicting accurately the house prices? Or do we just care about minimizing the overall error?
In all these metrics, the building block is the residual, which is the difference between predicted values and actual values.
MAE

The Mean Absolute Error calculates the average absolute residuals.
It doesn’t penalize high errors as much as other evaluation metrics. Every error is treated equally, even the errors of outliers, so this metric is robust to outliers. Moreover, the absolute value of the differences ignores the direction of error.
MSE
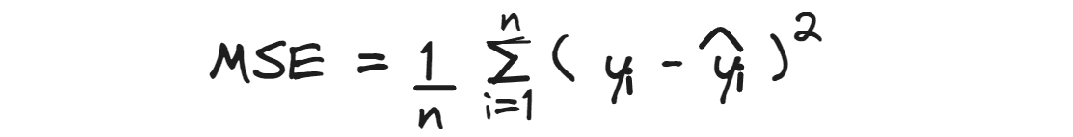
The Mean Squared Error calculates the average squared residuals.
Since the differences between predicted and actual values are squared, It gives more weight to higher errors,
so it can be useful when big errors are not desirable, rather than minimizing the overall error.
RMSE
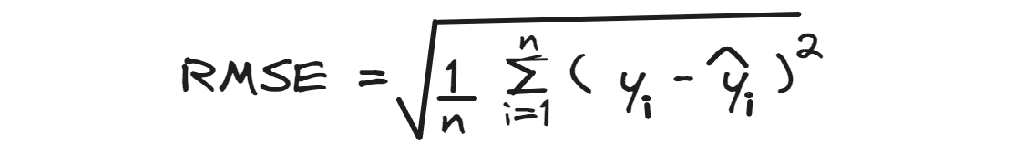
The Root Mean Squared Error calculates the square root of the average squared residuals.
When you understand MSE, you keep a second to grasp the Root Mean Squared Error, which is just the square root of MSE.
The good point of RMSE is that it is easier to interpret since the metric is in the scale of the target variable. Except for the shape, it’s very similar to MSE: it always gives more weight to higher differences.
MAPE
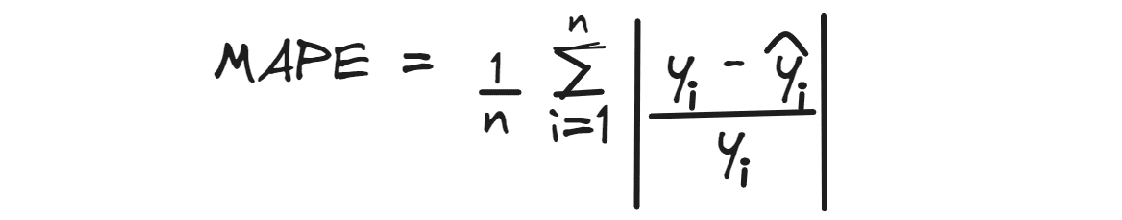
Mean Absolute Percentage Error calculates the average absolute percentage difference between predicted values and actual values.
Like MAE, it disregards the direction of the error and the best possible value is ideally 0.
For example, if we obtain a MAPE with a value of 0.3 for predicting house prices, it means that, on average, the predictions are below of 30%.
Final Thoughts
I hope that you have enjoyed this overview of the evaluation metrics. I just covered the most important measures for evaluating the performance of classification and regression models. If you have discovered other life-saving metrics, that helped you on solving a problem, but they are not nominated here, drop them in the comments.
Eugenia Anello is currently a research fellow at the Department of Information Engineering of the University of Padova, Italy. Her research project is focused on Continual Learning combined with Anomaly Detection.
